【堆和优先级队列】
目录
二叉堆
堆的代码实现
最大堆代码实现
向最大堆中添加一个元素—siftUp操作
删除堆顶元素—siftDown操作
测试代码方法
heapify 堆化
优先级队列
自定义类型的优先级队列实现
Comparator接口——比较器
二叉堆
堆有很多种存储形式，二叉堆就是其中的一种，所谓二叉堆，就是一颗完全二叉树，二叉堆分为两种：
- 最大堆 / 大根堆 ：根节点值 >= 子树的节点值
- 最小堆 / 小根堆 ： 根节点值 <= 子树的节点值
注意：在最大堆中，只能保证当根节点 >= 子树的所有节点，在任意子树中仍然满足这个特点，并不是说节点所在的层越高（根节点为最高层）值就越大。最小堆同理。但是堆中的中堆顶元素就是最值这句话是对的。
堆的代码实现
完全二叉树和满二叉树建议使用链表来存储，其他的二叉树不建议使用链表，所谓链表本质就是数组。完全二叉树和满二叉树存储没有空间的浪费，而普通节点为了区分左右子树，必须花费空间来存储空节点。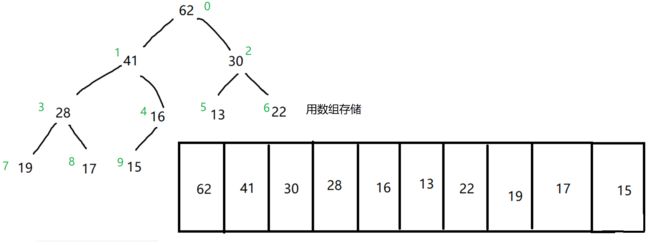
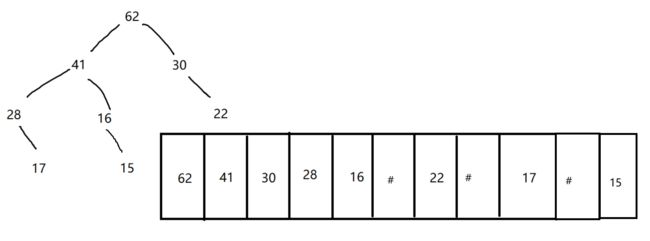那么使用顺序表存储完全二叉树时，根节点从0开始编号，给出一个节点k，如何仅用索引就能判断k节点是否有子树呢？
- 左子树的索引为 2*k +1
- 右子树的索引为 2*k + 2
根据这两个公式，我们就可以知道，当 2*k +1 < 数组长度时，就说明该节点有子树。
那么我们又如何用索引判断k节点是否有父节点呢？我们知道，在二叉树中，只有根节点没有父节点，所以只需要：父节点编号 > 0就说明有父节点
- 父节点索引为 ( k - 1 ) / 2
最大堆代码实现
//基于整型的最大堆实现
//根节点从0开始编号
public class MaxHeap {
//使用动态数组来存储最大堆
List data;
public MaxHeap(){
//构造方法的this调用
this(10);
}
//初始化的堆大小
public MaxHeap(int size){
data = new ArrayList<>(size);
}
//判断是否为空
public boolean isEmpty(){
return data.size() == 0;
}
//根据索引找父节点的索引
private int parant(int k){
return (k - 1) >> 1;
}
// //根据索引找左子树的索引
private int leftChild(int k){
return (k << 1) +1;
}
// //根据索引找左子树的索引
private int rightChild(int k){
return (k << 1) +2;
}
//查看最大值
public int peekMax(){
if (isEmpty()){
throw new NoSuchElementException("heap is empty!");
}else {
//返回堆顶元素
return data.get(0);
}
}
}
向最大堆中添加一个元素—siftUp操作
若在数组末尾添加，这棵树仍然是完全二叉树，但是它却不满足最大堆的性质
此时，我们使用siftUp( int k ) : 向上调整，也就是元素的上浮操作，使其仍然满足最大堆的性质。方法就是将插入的节点不断和它的父节点作比较，若值大于父节点就将二者位置互换。终止条件就是当前节点 <= 父节点，或者元素已经成了根节点。
代码实现：（接上述最大堆代码实现）
//向最大堆中添加一个元素
public void addVal(int val){
//1.直接在数组末尾添加元素
data.add(val);
//2.进行元素的上浮操作
siftUp(data.size() -1);
}
//元素上浮操作
private void siftUp(int k) {
//终止条件是走到根节点或者当前值小于父节点
while (k > 0 && data.get(k) > data.get(parant(k))){
//交换值
swap(k,parant(k));
k = parant(k);
}
}
//交换方法
private void swap(int i, int j) {
int temp = data.get(i);
data.set(i,data.get(j));
data.set(j,temp);
}
public String toString() {
return data.toString();
}代码测试：
public class HeapTest {
public static void main(String[] args) {
MaxHeap heap = new MaxHeap();
int[] arr = {62,41,30,28,16,13,22,19,17,15};
for (int num :arr){
heap.addVal(num);
}
heap.addVal(52);
System.out.println(heap);
}
}
//输出结果：[62, 52, 30, 28, 41, 13, 22, 19, 17, 15, 16]删除堆顶元素—siftDown操作
操作步骤是取出堆顶元素之后，将数组末尾的元素顶到堆顶，然后进行元素的下沉操作。
siftDown ( int k ):元素下沉操作，调整索引为k的节点不断下沉，和左右子树中的最大值互换。直到当前节点值 > 左右子树的值，或者到达了叶子节点，即2k+ 1 > size。
代码实现：
//取出最大值
public int extractMax(){
//判空
if(isEmpty()){
throw new NoSuchElementException("heap is empty!");
}
int max = data.get(0);
//1.将数组末尾元素顶到堆顶
data.set(0,data.get(data.size()-1));
//2.删除末尾元素
data.remove(data.size()-1);
//3.开始下沉操作
siftDown(0);
return max;
}
//元素的下沉操作，从位置k开始下沉
private void siftDown(int k) {
//还存在子树
while (leftChild(k) < data.size()){
//存左子树的索引
int j = leftChild(k);
//判断一下是否有右子树
if(j+1 < data.size() && data.get(j+1) > data.get(j)){
//此时右子数且大于左数的值
j = j+1;
}
//此时j为左右子树中的为最大值
if(data.get(k) >= data.get(j)){
//下沉结束
break;
}else {
swap(k,j);
//k变成子树中的最大值继续迭代
k = j;
}
}
}代码测试：
public static void main(String[] args) {
MaxHeap heap = new MaxHeap();
int[] arr = {62,41,30,28,16,13,22,19,17,15};
for (int num :arr){
heap.addVal(num);
}
heap.extractMax();
System.out.println(heap);
}
//测试结果：[41, 28, 30, 19, 16, 13, 22, 15, 17]如果将此最大堆不断的进行extractMax操作，我们将得到一个完全降序的数组：
public static void main(String[] args) {
MaxHeap heap = new MaxHeap();
int[] arr = {62,41,30,28,16,13,22,19,17,15};
for (int num :arr){
heap.addVal(num);
}
for (int i = 0; i < arr.length; i++) {
arr[i] = heap.extractMax();
}
System.out.println(Arrays.toString(arr));
}
//输出结果：[62, 41, 30, 28, 22, 19, 17, 16, 15, 13]测试代码方法
我们测试代码时通常在一个小集合上测试，这太片面了。以siftDown操作为例，生成一个10万数量的随机数，然后将这十万个数构建成最大堆，然后不断的extractMac(),如果代码正确，就将得到一个非递增的数组。
代码示例：
public static void main(String[] args) {
int[] data = new int[100000];
//生成随机数
ThreadLocalRandom random = ThreadLocalRandom.current();
for (int i = 0; i < data.length; i++) {
//范围是0到最大值的整数
data[i] = random.nextInt(0,Integer.MAX_VALUE);
}
MaxHeap heap = new MaxHeap();
for (int i : data){
heap.addVal(i);
}
//不断取出最大值
for (int i = 0; i < data.length; i++) {
data[i] = heap.extractMax();
}
System.out.println(isSorted(data));
}
//判断数组是否非递减
public static boolean isSorted(int[] arr){
for (int i = 0; i < arr.length - 1; i++) {
if (arr[i] < arr[i+1]){
return false;
}
}
return true;
}
//输出：trueheapify 堆化
将任意数组调整为最大堆，如何调整呢？
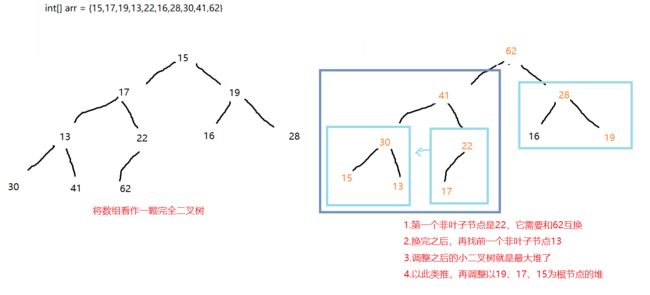
- 首先，任意的数组都可以看作一颗完全二叉树
- 从这颗完全二叉树的最后一个非叶子节点开始，进行元素的下沉操作即可
- 如何找到最后一个非叶子节点?最后一个非叶子节点就是最后一个叶子节点的父节点
- 那最后一个叶子节点何如找呢？最后一个叶子节点就是数组的最后一个元素
注意:调整是从底层往上调整的，所以上层的数字可能会调整多次 ，时间复杂度为O(n)
代码实现：
//将任意数组堆化
public MaxHeap(int[] arr){
//初始化
data = new ArrayList<>();
//1.先将所有元素复制到data数组中
for(int i : arr){
data.add(i);
}
//2.从最后一个非叶子节点进行siftDown
int lastParent = parant(data.size()-1);
for (int i = lastParent; i >= 0 ; i--) {
siftDown(i);
}
}
public class HeapTest {
public static void main(String[] args) {
int[] data = {15,17,19,13,22,16,28,30,41,62};
MaxHeap heap = new MaxHeap(data);
System.out.println(heap);
}
}
//输出结果：[62, 41, 28, 30, 22, 16, 19, 15, 13, 17]优先级队列
我们通常需要按照优先级情况对待处理对象进行处理，比如我们经常说事情要分轻重缓急，我们对要处理的事情进行了排序，处理优先级最高的事情时，也可能有新的事情需要处理。但是优先级队列虽然看起来是一个队列，但是它处理的元素个数是动态的，有进有出，不像排序处理的元素个数是固定的，因此它的底层是基于堆的实现。
| 入队 | 出队(出最大值 | |
|---|---|---|
| 普通队列，基于链表的 | O( 1 ) | O((N) |
| 优先级队列：堆 | O( logN ) | O(logN) 虽然堆顶就是最大值，但取出最大值后还需要进行siftDown操作 |
代码实现：
//基于最大堆的优先级队列
//队首元素就是优先级最大的元素，也就是值最大
public class PriorityQueue implements Queue {
private MaxHeap heap;
public PriorityQueue(){
heap = new MaxHeap();
}
@Override
//入队
public void offer(Integer val) {
heap.addVal(val);
}
@Override
//出队
public Integer poll() {
return heap.extractMax();
}
@Override
//取队首
public Integer peek() {
return heap.peekMax();
}
@Override
//判断是否为空
public boolean isEmpty() {
return heap.isEmpty();
}
}
JDK中的优先级队列默认是最小堆的实现
import article.Queue;
import java.util.Arrays;
public class PriorityQueueTest {
public static void main(String[] args) {
int[] arr = {1, 3, 2, 6, 5, 8, 10, 4, 7, 9};
Queue queue = new PriorityQueue();
//依次入队
for (int i : arr) {
queue.offer(i);
}
int[] ret = new int[arr.length];
//依次出队
for (int i = 0;i < arr.length;i++){
ret[i] = queue.poll();
}
System.out.println(Arrays.toString(ret));
}
}
//输出：[10, 9, 8, 7, 6, 5, 4, 3, 2, 1] 上述代码是将我们自己定义的优先级队列依次取出队首元素，可以看到得到的是一个降序数组 ，注意我们导入的是自己定义的队列和优先级队列。现在我们将导入的包换成JDK自己定义的：
可以看到输出的是一个升序数组，这就是因为JDK默认实现的是最小堆
自定义类型的优先级队列实现
上面我们实现了基本类型，那么自定义类型如何实现呢？首先我们要让自定义类型具有可比较的能力，以前我们了解过Comparable接口，现在我们使用它来实现：
public class Student implements Comparable{
private String name;
private int age;
public Student(String name,int age){
this.name = name;
this.age = age;
}
public String toString(){
return "Student{" +
"name=" + name+'\''+ ",age="+ age + '}';
}
@Override
public int compareTo(Student o) {
return this.age - o.age;
}
}
import article.Student;
import java.util.Queue;
import java.util.PriorityQueue;
import java.util.Arrays;
public class PriorityQueueTest {
public static void main(String[] args) {
Queue queue = new PriorityQueue<>();
Student s1 = new Student("张三",20);
Student s2 = new Student("李四",40);
Student s3 = new Student("王五",30);
queue.offer(s1);
queue.offer(s2);
queue.offer(s3);
System.out.print(queue.poll()+ " ");
System.out.print(queue.poll()+ " ");
System.out.print(queue.poll()+ " ");
}
}
//输出结果：Student{name=张三',age=20} Student{name=王五',age=30} Student{name=李四',age=40} 可以看到，连续出队是按年龄从小到大出队的，这就是自定义类型的最小堆。
在实际应用中，按照年龄优先级排列有时候是年龄小的优先，有时是年龄大的优先，上述代码实现的是年龄小优先级高，那么按照年龄大怎么写呢，我们只需将覆写的ComparableTo方法做以下修改：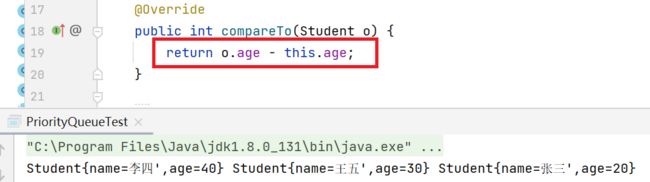
将 o 和 this 的位置调换就达到了我们的目的，这是为什么呢？根据返回值大小来排序，现在我们互换了当前对象和传入对象的位置，使小的变成“大的”，使大的反而“变小”。但是在实际应用中根据实际要求频繁的修改代码是不提倡的。此时我们就引出了另外一个接口：
Comparator接口——比较器
需要比较的类并不需要实现此接口，而是有一个专门的类实现接口，这个类就是为了进行Student的大小比较的
public class Student {
private String name;
private int age;
public Student(String name,int age){
this.name = name;
this.age = age;
}
public int getAge(){
return age;
}
public String toString(){
return "Student{" +
"name=" + name+'\''+ ",age="+ age + '}';
}
// 升序，谁大谁在前
static class StudentCom implements Comparator{
@Override
public int compare(Student o1, Student o2) {
return o1.getAge() - o2.getAge();
}
}
//降序，谁大谁在前
static class StudentComDesc implements Comparator{
@Override
public int compare(Student o1, Student o2) {
return o2.getAge() - o1.getAge();
}
}
}
public class PriorityQueueTest {
public static void main(String[] args) {
Student s1 = new Student("张三", 20);
Student s2 = new Student("李四", 40);
Student s3 = new Student("王五", 30);
Student[] students = {s1, s2, s3};
Arrays.sort(students, new Student.StudentCom());
System.out.println(Arrays.toString(students));
Arrays.sort(students,new Student.StudentComDesc());
System.out.println(Arrays.toString(students));
}
}
//输出；
[Student{name=张三',age=20}, Student{name=王五',age=30}, Student{name=李四',age=40}]
[Student{name=李四',age=40}, Student{name=王五',age=30}, Student{name=张三',age=20}] 以上就是使用 Comparator接口，实现我们想要的排序，比Comparable接口更加灵活。接下来我们来使用该接口实现最大堆和最小堆：
public class PriorityQueueTest {
public static void main(String[] args) {
//通过构造方法传入比较器
Queue queue = new PriorityQueue<>(new Student.StudentCom());
Student s1 = new Student("张三", 20);
Student s2 = new Student("李四", 40);
Student s3 = new Student("王五", 30);
queue.offer(s1);
queue.offer(s2);
queue.offer(s3);
while (!queue.isEmpty()){
System.out.print(queue.poll() + " ");
}
}
}
//输出：Student{name=张三',age=20} Student{name=王五',age=30} Student{name=李四',age=40} 上述实现的是最小堆，也就是值越小，优先级越高，若想要改造成最大堆，只需要传入我们定义的StudentComDesc类即可。
主方法第一句也可以变成下图这样，和上述代码是等价的。就是创建了一个Comparator接口的子类，这个子类只使用一次。
主方法也可以换成 这样：
我们所使用到的比较接口和匿名内部类的链接如下，感兴趣的可以去看看哦
| Comparable接口 | 抽象类和接口 |
| 匿名内部类 | 初识JAVA内部类 |