【数据库专题】智多星带你五分钟攻略“关系代数”——《狗叫江湖》第二幕续集

、
“百分百无规则教学时间！”

兄弟萌晚上好！我是无规则教学创始人【东星耀杨】，感谢兄弟萌对我的不离不弃，爱你们熬爱你们！还望兄弟萌给为师一个三连支持，要不然我蒸滴会紫砂的！

1️⃣作者简介

作者简介：东星耀杨，C站煮播之星，骚话专家，曾奉太上老君之名下凡，为了给迷途中的兄弟萌指点迷津，帮助兄弟萌早日踏入如我这般境界！世人见我，皆称之“王霸之气侧漏”的男人，哇靠蒸滴c！c了兄弟萌！
往期回顾：【耀杨的罗曼史】小红：耀杨欧巴，能教教我hashmap吗？【雀氏润】
耀杨和兄弟萌的约定：等我到一千粉，给兄弟萌发红包！感谢兄弟萌的陪伴和支持！

1️⃣《我要进场了》

兄弟萌兄弟萌~几时不见如隔三秋呀，没有兄弟萌的日子里为师只能靠刷剧度日，要不然都会腰腿酸痛，思念成疾的呀！爱你们熬爱你们！！！

2️⃣小粉丝提问

最近总是有兄弟私信耀杨，啥时候更新【数据库专题】呀，兄弟萌不是我不想更新，mdC失灵了，为师这脑回路也越发迟钝，一直想等着精神好点再给兄弟萌安排，这不它来了！

今日咱们不多说骚话，就是教学好吧兄弟萌，就这么定了！

1️⃣关系操作

在讲解关系代数之前，有必要先跟兄弟萌讲讲关系操作。

2️⃣关系模型中常用的关系操作

关系模型中常用的关系操作主要包括查询（query）操作和插入（insert）、删除（delete）、修改（update）操作两大部分。

3️⃣查询操作

- 关系的查询操作表达能力最强，是关系操作中最主要的操作
- 关系操作可以分为选择、投影、除、并、差、交、笛卡尔积等等。
- 查询操作的5种基本操作：选择、投影、并、差、笛卡尔积。

2️⃣关系操作的特点

⭐️关系操作的特点：集合操作方式，即操作的对象和结果均是集合，这种操作方式也成为一次一集合的方式

1️⃣关系代数

⭐️关系操作简单了解即可，下面为师带着你们攻略数据库原理中的关系代数！！

2️⃣关系代数是什么？

关系代数是一种抽象的查询语言，它用对关系的运算来表达查询。

所谓运算就是将运算符作用在某一个运算对象上得出运算结果，所以在这里运算的三大要素显而易见：运算对象、运算符和运算结果。

那么对于关系代数呢？这里为师本来想卖个关子，但是还是决定直接说吧，时间紧迫，今晚为师还想给兄弟萌更新一篇教学呢!

对于关系代数而言，运算对象是关系，运算结果同样为关系，而藏在这里的运算符主要分为两类：

1.集合运算符 并、差、交、笛卡尔积

2.专门的关系运算符 选择、投影、连接、除

接下来为师一一为兄弟萌讲解

2️⃣集合运算符

3️⃣并

公式：R ∪ S = { t | t∈R ∨ t∈S }（t∈S表示t是关系S的一个元组）

注：结果仍然是n目关系，由属于R或者S的元组组成。

3️⃣交

公式：R ∩ S = { t | t∈R ∧ t∈S }

注：结果是关系R和S形同的元组

3️⃣差

公式：R - S = { t | t∈R ∧ ¬t∈S }

注：结果是关系R减去R和S的交集

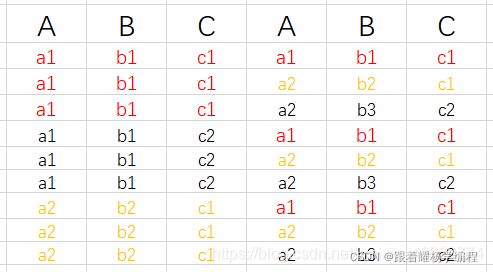
3️⃣笛卡尔积

公式：R × S = { tr⌒ts| tr∈R ∧ ts∈S }

注：

之间为师跟兄弟萌讲过域的笛卡尔积为基数相乘，集合的笛卡尔积也同理。
两个关系中的元组个数相乘得出结果关系的元组个数。

两个关系的目数之和为结果关系的目数

2️⃣专门的关系运算

3️⃣选择

公式：σF( R ) = { t | t∈R ∧ F(t) = ‘真’ }

注：选择是单目运算，是在行上进行的运算，根据一定的条件从关系R中选择若干个元组，组成一个新的关系。
单目查询到符合σ条件的元素，结果取元素所对应的元组（行）。

3️⃣投影

公式：∏A( R ) = { t[A]| t∈R }

注：投影同样是单目运算，是在垂直关系即列航进项的运算， 单目查询到符合条件的属性，取出属性所对应的列，去除该列中重复的元组。

3️⃣综合选择和投影运算的例子

∏_（TNo）（σ_{（cN=‘C5’）}（TC））

代表着讲授C5课程的教师号。

3️⃣连接

等值连接

• θ连接运算是一个二元运算，其效果是从两个关系R和S的笛卡尔积中选取满足连接条件的元组，而后组成新的关系。
• 设两个关系R和S，它们的属性列数分别为n和m，其中R中的属性可以进一步分解为属性集Z和X，即R=(Z，X)，关系S可以进一步分解为属性集W和Y，即S=(W，Y)。
• 如果我们认定X和Y是连接属性(需要X和Y的属性列数相等)，那么关系R和S在连接属性X和Y上的θ连接，就是在R和S的笛卡尔积中选择那些X属性集上的分量与Y属性集上的分量满足θ比较条件的那些元组。
• 新关系的列数为(n+m)，即两个关系的列数和，记作：

注意看为师细节：其中θ代表的是一个算术比较运算符，称为θ连接。XθY是连接条件：

θ为"=“时，称为等值连接；
θ为”<“时，称为小于连接；
θ为”>"时，称为大于连接；

根据连接定义可以推断出这样一个公式：
： R ⋈_AθBS=σ_(AθB)(R×S)

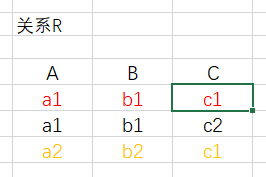
• 还有一种连接方式称为自然连接（是一种特殊的等值连接）
  它是在等值连接的情况下，当连接属性X和Y有着相同的属性列时，去掉连接结果中那些相同的属性列。

总结来说，自然连接是在广义笛卡尔积R×S中选出同名属性上符合相等条件的元组，再进行投影，去掉重复的同名属性，组成新的关系。

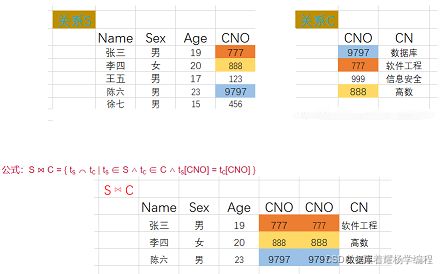
语法：R ⋈S = { tr ⌒ ts | tr ∈ R ∧ ts ∈ S ∧ tr[A] = ts[A] }

根据上面图，自然连接就是去除一个CNO属性列。

▶️自然连接与等值连接之间的联系与区别

⊙自然连接要求同名同域的属性组才可连接，而等值连接仅要求域相同；
⊙自然连接是去掉重复列的等值连接；
⊙自然连接一定是等值连接，而等值连接不一定是自然连接；
⊙自然连接后列的数量小于等于等值连接后列的数量。

▶️悬浮元组与外连接

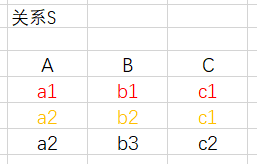
在关系S和C中被由于自然连接被舍弃的元组被称为悬浮元组。
S：


C：

• 将悬浮元组保存在结果关系中，并且在其他属性上填上空白纸NULL，这就叫做外连接。
• 如果只是保留左边关系S中的悬浮元组叫做左外连接。
• 如果只是保留右边关系C中的悬浮元组叫做右外连接。

3️⃣除

公式：R ÷ S = { tr[X] | tr∈R ∧ ∏y(S)⊆YX }

注：除法的运算比较抽象，在这里先简明一下定义：

关系R除以关系S的结果为关系T，则T中包含所有在R但是不在S的属性及其值，且T的元组与S的元组的所有组合都在R中。
用象集来定义除法：
给定关系R (X，Y) 和S (Y)，其中X，Y 为属性组。则R÷S得到一个新的关系P(X)：
如果R中某元组在X上分量值x的象集Yx包含S ， 则由x组成的元组就是P的元组。
R÷S = {x | S 真包含于 Yx }
Yx：x在R中的象集

定义总是那么难懂，为师给你简单说明下。
就是把被除的关系R去除与S中属性相等的列，列出剩余属性列的象集，与S在去除属性下的投影相比较，相同的则为除法的结果。

▶️象集

在下图中
a1的象集为{（b1，c2），（b2，c3），（b2, c1）}
a2到a4同理。找对应的B,C属性为象集中的一个元素。
▶️
▶️

在这里S在（B,C）上的投影为{（b1，c2），（b2，c3），（b2, c1）}

所以除法的结果为图（c）所示

《兄弟萌我爱你们！》

兄弟萌今天又是认真教学的一天，收获满满诶嘿，蒸滴c！！！
、
兄弟萌今天新学一招，三寸金莲漂a接菊花斩 ，哇靠爱你们哦爱你们！！！
、
兄弟萌临走之前，给兄弟萌透露一下，为师即将更新【寻找佳慧】专题，可以小小的期待一诶嘿 ~

、
航 空 母 舰！！！
~溜了溜了……