遗传算法求解TSP问题

一、导论

演化算法是一类模拟自然界遗传进化规律的仿生学算法，它不是一个具体的算法，而是一个算法簇。遗传算法是演化算法的一个分支，由于遗传算法的整体搜索策略和优化计算是不依赖梯度信息，所以它的应用比较广泛。

本次使用遗传算法（用Python编写）来解决TSP问题。

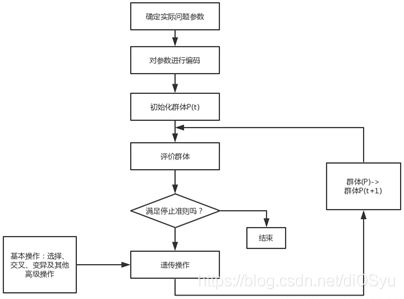
二、算法流程

（1）首先，对城市进行编号0，1，2，3……30。

（2）采用十进制编码：直接用城市的编号进行编码，染色体{0，1，2，……30}表示路径为0-1-2-……-30。

（3）参数设计：种群规模count=300，染色体长度length=31，进化次数epoch_time=2000。

       （4）初始化种群：为了加快程序的运行速度，在初始种群的选取中要选取一些较优秀的个体。使用改良圈算法求得一个较好的初始种群。随机生成一个染色体，比如{0，1，2，……30}，任意交换两城市顺序位置，如果总距离减小，则更新改变染色体，如此重复，直至不能再做修改。

       （5）采用次序交叉法。首先 随机地在双亲中选择两个杂交点，再交换杂交段，其他位置根据双亲城市的相对位置确定。

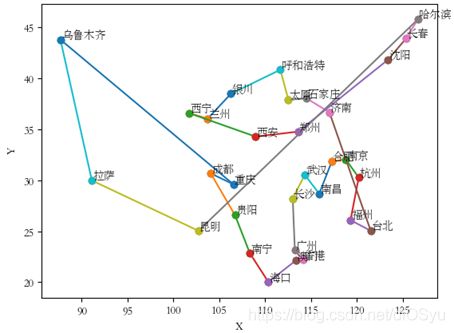
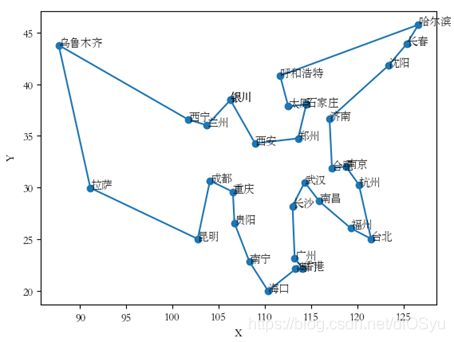
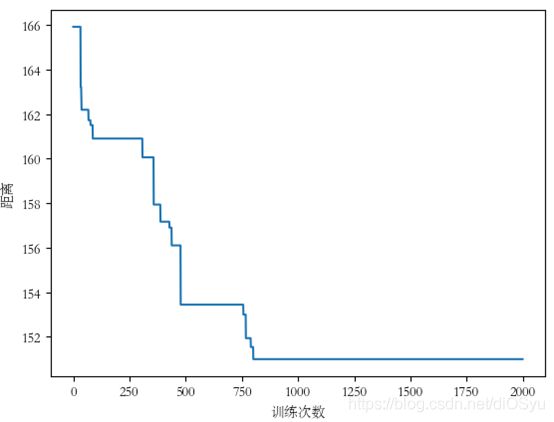
       （6）变异也是实现群体多样性的一种手段，同时也是全局寻优的保证。具体设计如下， 按照给定的变异率，对选定变异的个体，随机地取三个整数，满足 1

 

三、代码清单

文件	定位	作用
data.txt	数据文件	存放城市信息
main.py	主程序	程序入口，遗传算法求解TSP问题

data.txt：每一行为一条城市信息，第一列为城市名，第二列、第三列为城市横坐标、纵坐标。一共有31条城市信息。

重庆,106.54,29.59

拉萨,91.11,29.97

乌鲁木齐,87.68,43.77

银川,106.27,38.47

呼和浩特,111.65,40.82

南宁,108.33,22.84

哈尔滨,126.63,45.75

长春,125.35,43.88

沈阳,123.38,41.8

石家庄,114.48,38.03

太原,112.53,37.87

西宁,101.74,36.56

济南,117,36.65

郑州,113.6,34.76

南京,118.78,32.04

合肥,117.27,31.86

杭州,120.19,30.26

福州,119.3,26.08

南昌,115.89,28.68

长沙,113,28.21

武汉,114.31,30.52

广州,113.23,23.16

台北,121.5,25.05

海口,110.35,20.02

兰州,103.73,36.03

西安,108.95,34.27

成都,104.06,30.67

贵阳,106.71,26.57

昆明,102.73,25.04

香港,114.1,22.2

澳门,113.33,22.13

main.py：主程序

# -*- coding:utf-8 -*-



import numpy as np

import matplotlib.pyplot as plt

import matplotlib

import math

from random import random, randint, shuffle



# 设置字体

matplotlib.rcParams['font.family'] = 'STSong'



# 载入数据

def read_data():

    # 城市名

    _name = []

    # 城市坐标

    _condition = []

    # 读取数据

    with open('data.txt', 'r', encoding='utf-8') as f:

        lines = f.readlines()

        for line in lines:

            line = line.split('\n')[0]

            line = line.split(',')

            _name.append(line[0])

            _condition.append([float(line[1]), float(line[2])])

    _condition = np.array(_condition)

    return _name, _condition



class TSP:



    def __init__(self, _origin):

        # 起始点

        self.origin = _origin

        # 进化次数

        self.epochTime = 2000

        # 种群数

        self.populationCount = 300

        # 保持率

        self.retainRate = 0.3

        # 变异率

        self.mutationRate = 0.2

        # 改良次数

        self.improveCount = 10000

        # 读取数据

        self.cityNames, self.condition = read_data()

        # 城市数目

        self.cityCount = len(self.cityNames)

        # 生成距离矩阵

        self.mat = self.get_distance_matrix()

        # 城市索引

        self.cityIndex = [_ for _ in range(self.cityCount)]

        self.cityIndex.remove(_origin)



    # 距离矩阵

    def get_distance_matrix(self):

        # 使用短变量

        _cnt = self.cityCount

        _cdt = self.condition

        # 生成矩阵

        _mat = np.zeros([_cnt, _cnt])

        for i in range(_cnt):

            for j in range(i, _cnt):

                if i == j:

                    _mat[i][j] = 0

                else:

                    x2 = (_cdt[i][0] - _cdt[j][0]) ** 2

                    y2 = (_cdt[i][1] - _cdt[j][1]) ** 2

                    _mat[j][i] = _mat[i][j] = math.sqrt(x2 + y2)

        return _mat



    # 由路径求TSP路径总长度

    def get_total_distance(self, _x):

        # 使用短变量

        _mat = self.mat

        _origin = self.origin

        # 计算长度

        _dis = 0

        _dis += _mat[_origin][_x[0]]

        for _i in range(len(_x)):

            if _i == len(_x) - 1:

                _dis += _mat[_origin][_x[_i]]

            else:

                _dis += _mat[_x[_i]][_x[_i + 1]]

        return _dis



    # 生成一些较优秀的个体

    def improve(self, _x):

        # 改良次数

        improve_count = self.improveCount

        i = 0

        _dis = self.get_total_distance(_x)

        while i < improve_count:

            u = randint(0, len(_x) - 1)

            v = randint(0, len(_x) - 1)

            if u != v:

                new_x = _x.copy()

                t = new_x[u]

                new_x[u] = new_x[v]

                new_x[v] = t

                new_distance = self.get_total_distance(new_x)

                if new_distance < _dis:

                    _dis = new_distance

                    _x = new_x.copy()

            else:

                continue

            i += 1

        return _x



    # 自然选择

    def selection(self, _population):

        # 保持率

        retain_rate = self.retainRate

        # 对总距离从小到大进行排序

        graded = [[self.get_total_distance(_x), _x] for _x in _population]

        graded = [_x[1] for _x in sorted(graded)]

        # 选出适应性强的染色体

        retain_length = int(len(graded) * retain_rate)

        _parents = graded[:retain_length]

        # 设置弱者的存活概率

        random_select_rate = 0.2

        # 选出适应性不强，但是幸存的染色体

        for chromosome in graded[retain_length:]:

            if random() < random_select_rate:

                _parents.append(chromosome)

        return _parents



    # 交叉

    def crossover(self, _parents):

        # 生成子代的个数,保证种群数目稳定

        target_count = self.populationCount - len(_parents)

        # 孩子列表

        cs = []

        while len(cs) < target_count:

            male_index = randint(0, len(_parents) - 1)

            female_index = randint(0, len(_parents) - 1)

            if male_index != female_index:

                male = _parents[male_index]

                female = _parents[female_index]



                left = randint(0, len(male) - 2)

                right = randint(left + 1, len(male) - 1)



                # 交叉片段

                gene1 = male[left:right]

                gene2 = female[left:right]



                child1_c = male[right:] + male[:right]

                child2_c = female[right:] + female[:right]

                child1 = child1_c.copy()

                child2 = child2_c.copy()



                for o in gene2:

                    child1_c.remove(o)



                for o in gene1:

                    child2_c.remove(o)



                child1[left:right] = gene2

                child2[left:right] = gene1



                child1[right:] = child1_c[0:len(child1) - right]

                child1[:left] = child1_c[len(child1) - right:]



                child2[right:] = child2_c[0:len(child1) - right]

                child2[:left] = child2_c[len(child1) - right:]



                cs.append(child1)

                cs.append(child2)



        return cs



    # 变异

    def mutation(self, _cs):

        # 变异率

        mutation_rate = self.mutationRate

        # 生成变异后结果

        cs = []

        for i in range(len(_cs)):

            child = _cs[i]

            if random() < mutation_rate:

                u = randint(1, len(child) - 4)

                v = randint(u + 1, len(child) - 3)

                w = randint(v + 1, len(child) - 2)

                child = child[0:u] + child[v:w] + child[u:v] + child[w:]

            cs.append(child)

        return cs



    # 得到最佳纯输出结果

    def get_best_result(self, _population):

        graded = [[self.get_total_distance(_x), _x] for _x in _population]

        graded = sorted(graded)

        return graded[0][0], graded[0][1]



    # 进化

    def evolution(self):

        # 使用短变量

        _origin = self.origin

        # 初始化种群

        population = []

        for i in range(self.populationCount):

            # 随机生成个体

            x = self.cityIndex.copy()

            shuffle(x)

            # 优化个体

            x = self.improve(x)

            # 添加

            population.append(x)

        # 遗传优化

        register = []

        i = 0

        distance, result_path = self.get_best_result(population)

        while i < self.epochTime:

            # 选择繁殖个体群

            parents = self.selection(population)

            # 交叉繁殖

            cs = self.crossover(parents)

            # 变异操作

            cs = self.mutation(cs)

            # 更新种群

            population = parents + cs



            distance, result_path = self.get_best_result(population)

            register.append(distance)

            i += 1



        result_path = [_origin] + result_path + [_origin]

        # 输出

        print(distance)

        print(result_path)

        print(register)

        # 绘图

        xs = list()

        ys = list()

        _names = self.cityNames

        _condition = self.condition

        for j in result_path:

            # 画注解

            plt.annotate(_names[j], [_condition[j, 0], _condition[j, 1]])

            xs.append(_condition[j, 0])

            ys.append(_condition[j, 1])

        # 绘图

        plt.xlabel('X')

        plt.ylabel('Y')

        plt.plot(xs, ys, '-o')

        plt.show()

        plt.xlabel('训练次数')

        plt.ylabel('距离')

        plt.plot(list(range(len(register))), register)

        plt.show()



if __name__ == '__main__':

    t1 = TSP(3)

    t1.evolution()

 

四、运行结果

贪心法求解TSP问题（用于与遗传算法比较）：

       起点为城市0，最短长度为188.23。路径为：0-> 26-> 27-> 5-> 23-> 30-> 29-> 21-> 19-> 20-> 18-> 15-> 14-> 16-> 17-> 22-> 12-> 9-> 10-> 4-> 3-> 24-> 11-> 25-> 13-> 8-> 7-> 6-> 28-> 1-> 2-> 0。

遗传算法求解TSP问题

运行结果1：

       起点城市为3，最短路径长度为150.98。路径为：[3, 24, 11, 2, 1, 28, 26, 0, 27, 5, 23, 30, 29, 21, 19, 20, 18, 17, 22, 16, 14, 15, 12, 8, 7, 6, 4, 10, 9, 13, 25, 3]。

       该结果为迭代次数为2000次时运行结果。

算法收敛情况如下：

       横坐标为遗传算法的训练次数，纵坐标为最短路径长度。

五、分析与思考

（1）算法评价

算法	优点	缺点
贪心法	计算量小，运行时间较短	答案固定，不能获得更加优秀的解
遗传算法	收敛条件不够明确、计算量大、运行时间长、很多参数的确定需要多次测试	与贪心法相比，可以获得更优的路径解
动态规划	点较少时，运行时间可以接受，可以获得最优解	点数目较多时，运行时间过长

 

（2）遗传算法分析

1） 遗传算法终止条件：

1. 当最优个体的适应度达到给定的阈值；
2. 最优个体的适应度和群体适应度不再上升；
3. 迭代次数达到预设的代数时，算法终止。

2） 可以通过分析算法收敛情况，修改迭代次数，减少计算量，提高运行效率。

3） 遗传算法解决TSP问题，收敛情况多种多样。可以通过修改起始点、多次运行获得更优的路径解。

（3）总结

由于遗传算法的整体搜索策略和优化计算是不依赖梯度信息，只需要影响搜索方向的目标函数和相应的适应度函数，所以它的应用比较广泛。

利用遗传算来进行大规模问题的组合优化是一种比较有效的方法，因为在目前的计算上利用枚举法求解最优解有一定的难度。

但是遗传算法也有不足之处，它对算法的精确度、可行度、计算复杂性等方面还没有有效的定量分析方法。

六、参考文献

[1] 遗传算法解决TSP问题. Springtostring.

https://blog.csdn.net/springtostring/article/details/82429604

[2] 遗传算法. 维基百科. https://zh.wikipedia.org/wiki/遗传算法