胖楠

机器学习有监督-分类算法

机器学习应用分析–有监督算法-分类算法

### 按学习方式分类：
监督学习
无监督学习
半监督学习
强化学习

①监督学习

数据集中的每个样本有相应的“正确答案”，根据这些样本做出预测，分有两类：回归问题和分类问题。

（ 1）回归问题举例

例如：预测房价，根据样本集拟合出一条连续曲线。

（ 2）分类问题举例

例如：根据肿瘤特征判断良性还是恶性，得到的是结果是“良性”或者“恶性”，是离散的。

监督学习：从给定的训练数据集中学习出一个函数（模型参数），当新的数据到来时，可以根据这个函数预测结果。监督学习的训练集要求包括输入输出，也可以说是特征和目标。训练集中的目标是由人标注的。

监督学习包含 分类问题/回归问题/降维（LDA）https://blog.csdn.net/sinat_30353259/article/details/81569550/集成学习（Ensemble Learning)

②无监督学习

无监督学习：输入数据没有被标记，也没有确定的结果。样本数据类别未知，需要根据样本间的相似性对样本集进行分类（聚类， clustering）试图使类内差距最小化，类间差距最大化。

实际应用中，不少情况下无法预先知道样本的标签，也就是说没有训练样本对应的类别，因而只能从原先没有样本标签的样本集开始学习分器设计

常见应用场景：聚类和数据降维

PCA和很多deep learning算法都属于无监督学习

③半监督学习

半监督学习：即训练集同时包含有标记样本数据和未标记样本数据。

④强化学习Qlearning

实质是： make decisions问题，即自动进行决策，并且可以做连续决策。

主要包含四个元素： agent，环境状态，行动，奖励；

强化学习的目标就是获得最多的累计奖励。

应用场景：强化学习目前还不够成熟，应用场景也比较局限。最大的应用场景就是游戏了。

一个典型的强化学习场景：

· 机器有一个明确的小鸟角色——代理

· 需要控制小鸟飞的更远——目标

· 整个游戏过程中需要躲避各种水管——环境

· 躲避水管的方法是让小鸟用力飞一下——行动

· 飞的越远，就会获得越多的积分——奖励

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dfO3SVQ7-1644566845678)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210418200641691.png)]

一有监督之分类问题

分类问题：

感知机（perceptron）
KNN算法
决策树
朴素贝叶斯
logistic回归
支持向量机SVM

1.1感知机（perceptron）

2.1.1应用场景：

2.1.2算法思想：

二类分类的线性分类模型，是神经网络和支持向量机的基础。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-PDvLJYjT-1644566845679)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210730180715905.png)]

2.1.3 计算流程：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-KekvZWxn-1644566845680)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210730181021983.png)]

1.1 k-近邻（KNN）算法

1.1.1 应用场景:

有字符识别、文本分类、图像识别等领域。

需要一个特别容易解释的模型的时候。比如需要向用户解释原因的推荐算法。

1.1.2算法思想：

一个样本与数据集中的k个样本最相似，如果这k个样本中的大多数属于某一个类别，则该样本也属于这个类别。

1.1.3计算流程：

1）计算已知类别数据集中的点与当前点之间的距离
2）按距离递增次序排序
3）选取与当前点距离最小的k个点
4）统计前k个点所在的类别出现的频率
5）返回前k个点出现频率最高的类别作为当前点的预测分类

优点：

1、简单有效
2、重新训练代价低
3、算法复杂度低
4、适合类域交叉样本
5、适用大样本自动分类

缺点：

1、惰性学习
2、类别分类不标准化
3、输出可解释性不强
4、不均衡性
5、计算量较大

1.1.4 调包实战

例子1[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eHOHjT9T-1644566845680)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417091937644.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Yvl2WN8h-1644566845680)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417092035779.png)]

import math
movie_data = {"宝贝当家": [45, 2, 9, "喜剧片"],
              "美人鱼": [21, 17, 5, "喜剧片"],
              "澳门风云3": [54, 9, 11, "喜剧片"],
              "功夫熊猫3": [39, 0, 31, "喜剧片"],
              "谍影重重": [5, 2, 57, "动作片"],
              "叶问3": [3, 2, 65, "动作片"],
              "伦敦陷落": [2, 3, 55, "动作片"],
              "我的特工爷爷": [6, 4, 21, "动作片"],
              "奔爱": [7, 46, 4, "爱情片"],
              "夜孔雀": [9, 39, 8, "爱情片"],
              "代理情人": [9, 38, 2, "爱情片"],
              "新步步惊心": [8, 34, 17, "爱情片"]}

# 测试样本  唐人街探案": [23, 3, 17, "？片"]
#下面为求与数据集中所有数据的距离代码：
x = [23, 3, 17]
KNN = []
for key, v in movie_data.items():
    d = math.sqrt((x[0] - v[0]) ** 2 + (x[1] - v[1]) ** 2 + (x[2] - v[2]) ** 2)
    KNN.append([key, round(d, 2)])

# 输出所用电影到 唐人街探案的距离
print(KNN)

#按照距离大小进行递增排序
KNN.sort(key=lambda dis: dis[1])

#选取距离最小的k个样本，这里取k=5；
KNN=KNN[:5]
print(KNN)

#确定前k个样本所在类别出现的频率，并输出出现频率最高的类别
labels = {"喜剧片":0,"动作片":0,"爱情片":0}
for s in KNN:
    label = movie_data[s[0]]
    labels[label[3]] += 1
labels =sorted(labels.items(),key=lambda l: l[1],reverse=True)
print(labels,labels[0][0],sep='\n')

调包实战—例子2

糖尿病预测

（数据链接：https://pan.baidu.com/s/1gqaGuQ9kWZFfc-SXbYFDkA 密码：lxfx）
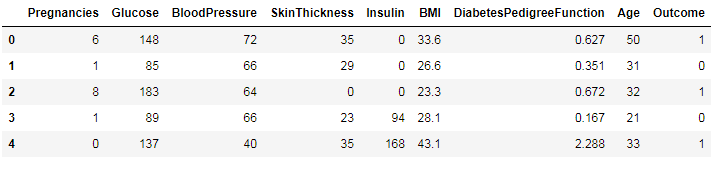
import numpy as np
import pandas as pd
#读入数据
data = pd.read_csv('data/pima-indians-diabetes/diabetes.csv')
data.head()

简单看下各字段的意思：

Pregnancies：怀孕的次数

Glucose：血浆葡萄糖浓度

BloodPressure：舒张压

SkinThickness：肱三头肌皮肤皱皱厚度

Insulin：胰岛素

BMI：身体质量指数

Dia…：糖尿病血统指数

Age：年龄

Outcone：是否糖尿病，1为是

我们把数据划分为特征和label，前8列为特征，最后一列为label。

X = data.iloc[:, 0:8]
Y = data.iloc[:, 8]
#切分数据集在模型训练前，需要将数据集切分为训练集和测试集（73开或者其它），这里选择82开，使用sklearn中model_selection模块中的train_test_split方法。
from sklearn.model_selection import train_test_split
X_train, X_test, Y_train, Y_test = train_test_split(X, Y, test_size=0.2, random_state=22)

这里的test_size为测试集的比例，random_state为随机种子，这里可设置任意数字，保证下次运行同样可以选择出对应的训练集和测试集

模型训练与评估

KNN算法使用sklearn.neighbors模块中的KNeighborsClassifier方法。常用的参数如下：

n_neighbors，整数，也就是k值。

weights，默认为‘uniform’；这个参数可以针对不同的邻居指定不同的权重，也就是说，越近可以权重越高，默认是一样的权重。‘distance’可以设置不同权重。

在sklearn.neighbors还有一个变种KNN算法，为RadiusNeighborsClassifier算法，可以使用一定半径的点来取代距离最近的k个点。
接下来，我们通过设置weight和RadiusNeighborsClassifier，对算法进行比较
from sklearn.neighbors import KNeighborsClassifier,RadiusNeighborsClassifier

model1 = KNeighborsClassifier(n_neighbors=2)
model1.fit(X_train, Y_train)
score1 = model1.score(X_test, Y_test)

model2 = KNeighborsClassifier(n_neighbors=2, weights='distance')
model2.fit(X_train, Y_train)
score2 = model2.score(X_test, Y_test)

model3 = RadiusNeighborsClassifier(n_neighbors=2, radius=500.0)
model3.fit(X_train, Y_train)
score3 = model3.score(X_test, Y_test)

print(score1, score2, score3)


#result
#0.714285714286 0.701298701299 0.649350649351

可以看出，还是默认情况的KNN算法结果最好。

交叉验证

通过上述结果可以看出：默认情况的KNN算法结果最好。这个判断准确么？答案是不准确，因为我们只是随机分配了一次训练和测试样本，可能下次随机选择训练和测试样本，结果就不一样了。这里的方法为：交叉验证。我们把数据集划分为10折，每次用9折训练，1折测试，就会有10次结果，求十次的平均即可。当然，可以设置cv的值，选择不同的折数。

from sklearn.model_selection import cross_val_score

result1 = cross_val_score(model1, X, Y, cv=10)
result2 = cross_val_score(model2, X, Y, cv=10)
result3 = cross_val_score(model3, X, Y, cv=10)

print(result1.mean(), result2.mean(), result3.mean())

# result
# 0.712235133288 0.67966507177 0.64976076555

1.2 决策树

有监督分类与回归算法

1.2.1应用场景：

作为一些更有用的算法的基石。
1、熵的例子：论坛流失性跟性别还是和活跃度有关
2、基尼的列子：拖欠贷款和是否有房、婚姻状况、收入的关联性
3、贷款风险评估
4、保险推广预测

1.2.2 算法思想：

决策树学习的目标：根据给定的训练数据集构建一个决策树模型，使它能够对实例进行正确的分类。
决策树学习的本质：从训练集中归纳出一组分类规则，或者说是由训练数据集估计条件概率模型。
决策树学习的损失函数：正则化的极大似然函数
决策树学习的测试：最小化损失函数
决策树学习的目标：在损失函数的意义下，选择最优决策树的问题。
决策树原理和问答猜测结果游戏相似，根据一系列数据，然后给出游戏的答案。

在树构造过程中，每次在样本特征集中选择最合适的特征作为分支节点，是决策树学习算法的核心，目标是使决策树能够准确预测每个样本的分类，且树的规模尽可能小。

算法原理：

如图所示，我们首先到底是通过天气、湿度还是风级来进行决策了？

熵

首先，我们看什么是熵。简单来说，熵是描述事物的混乱程度的（也可以说是不确定性）。例如：中国足球进入世界杯，这个不确定性可能是0，所以熵可能就是0；6面的色子的不确定性比12面色子的要低，所以熵也会比其低。现在就来看熵的公式： $\mathrm{H}=-\sum_{\mathrm{i}=1}^{\mathrm{n}} \mathrm{p}(\mathrm{xi}) \log _{2} \mathrm{p}(\mathrm{xi})$
那6面色子的熵： $1 / 6^{*} \log _{2} 1 / 6$ 的6倍，也就是2.585
以此类推，那12面的熵就是：3.585

最后，我们计算下该案例的信息熵：不打球为5，打球为9，因此熵计算为：

-(5/14 * log(5/14,2) + 9/14 * log(9/14,2))
0.940

信息增益 -ID3

到底先按哪个特征划分数据集呢?我们有个原则，就是将无序的数据变得有序，换句话说，就是让熵变小，变的越小越好。而信息增益就是划分数据集前后熵的变化，这里就是要让信息增益越大越好。
我们以天气为例，计算划分后的信息增益：

晴天时：2/5打球，3/5不打球，熵为：
-(2/5 * log(2/5,2) + 3/5 * log(3/5,2))
0.971
阴天熵：0

雨天熵：0.971

天气为晴天、阴天和雨天的概率为5/14，4/14和5/14，所以划分后的熵为：5/14 * 0.971+4/14 * 0+5/14 * 0.971得0.693，信息增益为0.940-0.693为0.247，同理可以求出其他特征的信息增益。
这里的天气信息增益最大，所以选择其为初始的划分依据。
选择完天气做为第一个划分依据后，能够正确分类的就结束划分，不能够正确分类的就继续算其余特征的信息增益，继续前面的操作，结果如图所示。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xHKHpnQZ-1644566845681)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210418184836026.png)]

信息增益比率 -C4.5

基尼系数GINI–CART

CART分类树算法使用基尼系数来代替信息增益比，基尼系数代表了模型的不纯度，基尼系数越小，则不纯度越低，特征越好。这和信息增益(比)是相反的

1.2.3计算流程：

1）开始：构建根节点，将所有训练数据都放在根节点，选择一个最优特征，按着这一特征将训练数据集分割成子集，使得各个子集有一个在当前条件下最好的分类。

2）如果这些子集已经能够被基本正确分类，那么构建叶节点，并将这些子集分到所对应的叶节点去。

3）如果还有子集不能够被正确的分类，那么就对这些子集选择新的最优特征，继续对其进行分割，构建相应的节点，如果递归进行，直至所有训练数据子集被基本正确的分类，或者没有合适的特征为止。

4）每个子集都被分到叶节点上，即都有了明确的类，这样就生成了一颗决策树

优点：

1、生成的决策树结果很直观
2、基本不需要预处理，不需要提前归一化，处理缺失值
3、既可以处理离散值也可以处理连续值
4、可以很容易处理分类问题
5、相比于神经网络之类的黑盒分类模型，决策树的可解释性很好
6、可以用交叉验证的剪枝来选择模型，从而提高泛化能力
7、对于异常值的容错能力号，健壮性高

缺点：

1、决策树算法容易过拟合
2、决策树会因为样本发生一点点的改动而导致结果变化
3、寻找最优的决策树是一个NP难的问题，容易陷入局部最优
4、有些复杂的关系，决策树很难学习到，例如异或关系
5、没有在线学习

1.2.4 调包实战——

2.2.4.1泰坦尼克号生还预测

[https://www.jianshu.com/p/8aee00ab196d]:

1.2.4.2 《银行贷款偿还的数据集构造分类器》

题：使用 scikit-learn 建立决策树为银行贷款偿还的数据集构造分类器，并评估分类器的性能。

数据预览

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-irK9NFR5-1644566845682)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417110637327.png)]

# # 决策树

#读入数据
import pandas as pd
filename = 'data/bankdebt.csv'
data = pd.read_csv(filename, nrows = 5, index_col = 0, header = None)
print(data.values)

#数据预处理，全部转化为数字
data = pd.read_csv(filename, index_col = 0, header = None)
data.loc[data[1] == 'Yes',1 ] = 1
data.loc[data[1] == 'No',1 ] = 0
data.loc[data[2] == 'Single',2 ] = 1
data.loc[data[2] == 'Married',2 ] = 2
data.loc[data[2] == 'Divorced',2] = 3
data.loc[data[4] == 'Yes',4 ] = 1
data.loc[data[4] == 'No',4 ] = 0

print(data.loc[1:5,:])

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aIBaIwXA-1644566845682)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417110858560.png)]

#取data前3列数据作为特征属性值,最后一列作为分类值
X = data.loc[ :, 1:3 ].values.astype(float)
y = data.loc[ :, 4].values.astype(int)
#训练模型，预测样本分类
from sklearn import tree
clf = tree.DecisionTreeClassifier()
clf = clf.fit(X, y)
clf.score(X,y)
#查看分类器分类结果
predicted_y = clf.predict(X)
predicted_y

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hTG9BhUC-1644566845683)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417111107859.png)]

#评估分类器性能,计算混淆矩阵，Precision 和 Recall
#分类性能报告和混淆矩阵计算
from sklearn import metrics
print(metrics.classification_report(y, predicted_y))
print('Confusion matrix:' )
print( metrics.confusion_matrix(y, predicted_y) )

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-zSPLVIu9-1644566845683)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417111245334.png)]

# 思考与练习
# 划分训练集
from sklearn import model_selection
X_train,X_test,y_train,y_test=model_selection.train_test_split(X,y,test_size=0.5,random_state=1)
#在训练集上学习模型
from sklearn import tree
clf = tree.DecisionTreeClassifier()
clf1 = clf.fit(X_train, y_train)
clf1.score(X_train, y_train)
clf1.score(X_test,y_test)
#在测试集上进行性能评估
y_test_pred=clf1.predict(X_test)
from sklearn import metrics
print(f"性能评估报告：\n{metrics.classification_report(y_test,y_test_pred)}")
print(f"混淆矩阵：\n{metrics.confusion_matrix(y_test,y_test_pred)}")

#分类器保存到文件中
import joblib
joblib.dump(clf1,'clf1.pkl')
#重新加载
import numpy as np
load_clf1=joblib.load('clf1.pkl')
new_x=np.array([[0,2,12]])
print(f"一个无房产，已婚，年收入12万的例子：{new_x}")
print(f"预期无法偿还债务否？{load_clf1.predict(new_x)}")

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HloAYSsc-1644566845684)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417111320445.png)]

1.3朴素贝叶斯

1.3.1 应用场景：

常用于文档的分类问题
是相对容易理解的一个模型，至今依然被垃圾邮件过滤器使用。
需要一个比较容易解释，而且不同维度之间相关性较小的模型的时候。可以高效处理高维数据，虽然结果可能不尽如人意。

1.3.2 算法思想：

选择具有最高概率的决策。

朴素：假设特征间相互独立
朴素+贝叶斯
贝叶斯公式

$P (A k ∣ B) = (\sum P (B ∣ A i ) * P (A i )) / (P (B ∣ A k ) * P (A k ))$

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xbcFjdom-1644566845684)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417132100699.png)]

朴素贝叶斯公式：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-oG3Peq1f-1644566845684)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417132303851.png)]

1.3.3 计算流程

朴素贝叶斯是生成模型。

生成模式和判别模式的区别：
生成模式：由数据学得联合概率分布，求出条件概率分布P(Y|X)的预测模型；
常见的生成模型有：朴素贝叶斯、隐马尔可夫模型、高斯混合模型、文档主题生成模型（LDA）、限制玻尔兹曼机
判别模式：由数据学得决策函数或条件概率分布作为预测模型
常见的判别模型有：K近邻、SVM、决策树、感知机、线性判别分析（LDA）、线性回归、传统的神经网络、逻辑斯蒂回归、boosting、条件随机场

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Ekttkhq9-1644566845685)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417133343810.png)]
$$
1

,a
2

,…,a
m
$$
那么x就属于Yk的分类。

朴素贝叶斯的优缺点

优点：对小规模的数据表现很好，适合多分类任务，适合增量式训练。
缺点：对输入数据的表达形式很敏感（离散、连续，值极大极小之类的）。

1.3.4 调包实战——

1.3.4.1文档处理

TF-IDF方法：将文本数据转换为数字，是一种统计方法，用来评估单个单词在文档中的重要程度。

TF表示词频，对一个文档而言，词频就是词在文档出现的次数除以文档的词语总数。例如：一篇文档有1000个字，“我”字出现25次，那就是0.025；“Python”出现5次就是0.005。

IDF表示一个词的逆向文档频率指数。可以由总文档数除以包含该词出现的文档数目，然后取对数。例如：有10000个文档，“Python”只出现了10篇文章，则IDF=log(10000/10)=3；“我”字在所有文档都出现过，则IDF为0。

词频和权重指数相乘，就是词在文档中的重要程度。可以看出，词语的重要性随它在 文档中 出现的次数呈正比例增加，但同时会随着它在 语料库 中出现的频率呈反比下降。

主要代码演示：

#模型训练
from sklearn.naive_bayes import MultinomialNB
y_train = news_train.target
clf = MultinomialNB(alpha=0.0001)
clf.fit(X_train, y_train)
train_score = clf.score(X_train, y_train)

# result 
# 0.99787556904400609

#模型评估
news_test = load_files('data/379/test')
X_test = vect.transform(news_test.data)
y_test = news_test.target

clf.score(X_test, y_test)

# result 
# 0.90881728045325783

#我们也可以通过classification_report方法来查看全方位的评价。
from sklearn.metrics import classification_report

pred = clf.predict(X_test)

print(classification_report(y_test, pred, target_names=news_test.target_names))

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BE9SyRk0-1644566845685)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417135421484.png)]

也可以查看我们的混淆矩阵

from sklearn.metrics import confusion_matrix

cm = confusion_matrix(y_test, pred)

print(cm)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Yeh9Mn0P-1644566845686)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417135456727.png)]

1.3.4.2 《垃圾邮件分类》

本例从 Trec06 数据集中随机选取了 5000 封垃圾邮件和 5000 封正常邮件，预处理后得到 10000 条文本保存到“mailcorpus.txt”文件中（文件格式为 UTF-8），每封邮件正文在文件中保存为一行文本，其中前 5000 条为垃圾邮件，后 5000 条为正常邮件。“mailcorpus.txt”

文件格式如图所示。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9LUkmtWQ-1644566845686)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417140639928.png)]

import jieba
from sklearn.feature_extraction.text import CountVectorizer
#从文件读取文本，放入列表中
train_file = open("data/mailcorpus.txt", 'r', encoding = "utf-8")
corpus=train_file.readlines()   #列表中的每个元素为一行文本
corpus

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Bfmh4v7K-1644566845687)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417141032168.png)]

#分词
split_corpus = []
for c in corpus:
    split_corpus.append(" ".join(jieba.lcut(c)))
split_corpus
#使用词袋模型提取特征，得到文本特征矩阵
cv = CountVectorizer(token_pattern=r"(?u)\b\w+\b")
X = cv.fit_transform(split_corpus).toarray()
#构造标签向量，垃圾标签为0，正常标签为1
y = [0] * 5000 + [1] * 5000
y

#将特征集 分为训练集和测试集
from sklearn import model_selection
X_train, X_test, y_train, y_test = model_selection.train_test_split(X, y, test_size=0.4, random_state = 0)

#使用朴素贝叶斯训练分类模型，给出分类效果
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB()
gnb.fit(X_train,y_train)
y_pred = gnb.predict(X_test)

#朴素贝叶斯模型分类效果
print("naive_bayes accuracy:\n",gnb.score(X_test, y_test))
print("naive_bayes report:\n",metrics.classification_report(y_test, y_pred))
print("naive_bayes matrix:\n",metrics.confusion_matrix(y_test, y_pred))

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5Mc8wES6-1644566845687)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417145259000.png)]

1.4 逻辑斯蒂回归 (Logistic regression)

1.4.1应用场景：

应用领域：
1、预测是否发生、发生的概率（流失、客户响应等预测）
2、影响因素、危险因素分析（找出影响结果的主要因素）
3、判别、分类

1.4.2 算法思想

假设数据服从这个分布，然后使用极大似然估计做参数的估计。逻辑回归属于广义线性回归模型，广义线性回归模型有很多种类，比较常见的有以下几种，他们的主要区别在于因变量的不同：

当因变量Y的分布是二项分布（特别是0-1分布）的时候，称之为逻辑回归；

当因变量Y的分布是泊松分布，称之为泊松回归；

当因变量Y的分布是负二项分布，称之为负二项回归。

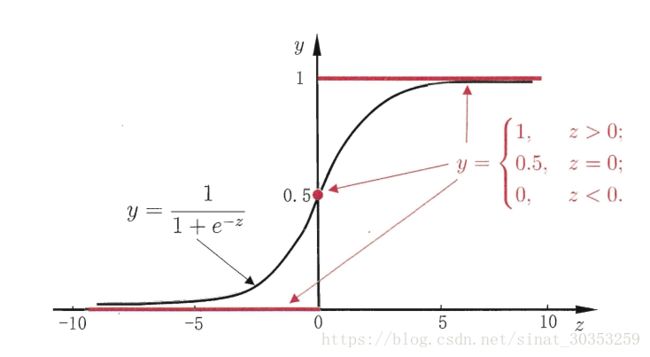
逻辑斯蒂概率分布函数就是我们逻辑斯蒂回归函数 $y=\frac{1}{1+e^{-z}}$ 。

1.4.3 计算流程

假设有一个二分类问题，输出为y∈{0,1}，而线性回归模型产生的预测值为 $z=w^{T} x+b$ 是实数值，我们希望有一个理想的阶跃函数来帮我们实现z值到0/1值的转化。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-paOMCsBq-1644566845687)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417152655616.png)]

然而该函数不连续，我们希望有一个单调可微的函数来供我们使用，于是便找到了Sigmoid function来替代,两者的图像如下图所示（图片出自文献2）

有了Sigmoid fuction之后，由于其取值在[0,1]，我们就可以将其视为类1的后验概率估计p(y=1|x)。说白了，就是如果有了一个测试点x，那么就可以用Sigmoid fuction算出来的结果来当做该点x属于类别1的概率大小。
于是，非常自然地，我们把Sigmoid fuction计算得到的值大于等于0.5的归为类别1，小于0.5的归为类别0.
$\hat{y}=\left\{\begin{array}{ll} 1 & \hat{p} \geq 0.5 \\ 0 & \hat{p} \leq 0.5 \end{array}\right.$
即逻辑斯蒂回归函数为：
$\hat{p}=\sigma\left(\theta^{T} \cdot x_{b}\right)=\frac{1}{1+e^{-\theta^{T} \cdot x_{b}}}$

损失函数

如果真实值y等于1，预测的p越小，即我们预测分类为0，说明我们预测的不太准，所以损失越大；

如果真实值y等于0，预测的p越大，即我们预测分类为1，说明我们预测的不太准，损失越大

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-eGXpszCo-1644566845688)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417164701354.png)]

损失数如下：

完整损失函数： $J(\theta)=-\frac{1}{m} \sum_{i=1}^{m} y^{(i)} \log \left(\hat{p}^{(i)}\right)+\left(1-y^{(i)}\right) \log \left(1-\hat{p}^{(i)}\right)$

优化

用梯度下降法：

目标是找到损失函数的最小值，找到每次迭代后下降最快的地方，即求导，沿导数相反方向移动、迭代，直至收敛。

通过调整权重参数w和b，使得譬如p=0.4就让它能越来越接近0；p=0.6就让它越来越接近1。

优点：

实现简单，广泛的应用于工业问题上；
简单易于理解，直接看到各个特征的权重
能容易地更新模型吸收新的数据
对逻辑回归而言，多重共线性并不是问题，它可以结合L2正则化来解决该问题；
适用于大规模数据集

缺点：

对数据和场景的适应能力有局限性，不如决策树算法适应性那么强。
当特征空间很大时，逻辑回归的性能不是很好；
容易欠拟合，一般准确度不太高
不能很好地处理大量多类特征或变量；
只能处理两分类问题（在此基础上衍生出来的softmax可以用于多分类），且必须线性可分，对于非线性特征，需要进行转换；
使用前提: 自变量与因变量是线性关系。
只是广义线性模型，不是真正的非线性方法。

softmax

在机器学习尤其是深度学习中，softmax是个非常常用而且比较重要的函数，尤其在多分类的场景中使用广泛。他把一些输入映射为0-1之间的实数，并且归一化保证和为1，因此多分类的概率之和也刚好为1。
首先我们简单来看看softmax是什么意思。顾名思义，softmax由两个单词组成，其中一个是max。对于max我们都很熟悉，比如有两个变量a,b。如果a>b，则max为a，反之为b。用伪码简单描述一下就是 if a > b return a; else b。
另外一个单词为soft。max存在的一个问题是什么呢？如果将max看成一个分类问题，就是非黑即白，最后的输出是一个确定的变量。更多的时候，我们希望输出的是取到某个分类的概率，或者说，我们希望分值大的那一项被经常取到，而分值较小的那一项也有一定的概率偶尔被取到，所以我们就应用到了soft的概念，即最后的输出是每个分类被取到的概率。

1.4.4 调包实战——乳腺癌检测

数据导入

本次实战使用sklearn中的数据集，如图所示。

from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
print(cancer.DESCR)

#切分数据集
X = cancer.data
y = cancer.target

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=33)

模型训练与评估

逻辑回归算法使用sklearn.linear_model 模块中的LogisticRegression方法。常用的参数如下：

penalty：设置正则化项，其取值为’l1’或’l2’，默认为’l2’。
C：正则化强度，C越大，权重越小

from sklearn.linear_model import LogisticRegression

model = LogisticRegression()
model.fit(X_train, y_train)
model.score(X_test, y_test)

# result
# 0.94736842105263153

#我们换为L1范数
model2 = LogisticRegression(penalty='l1')
model2.fit(X_train, y_train)
model2.score(X_test, y_test)

# result
# 0.95614035087719296

逻辑回归的参数：回归系数和偏置

print(model2.coef_)
print(model2.intercept_)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-h2iq4YSc-1644566845688)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417170920549.png)]

1.5 支持向量机SVM

1.5.1应用场景：

机器视觉：
1、行人检测及目标识别
2、病理诊断
数据挖掘：
1、基因序列检测
2、生物蛋白质检测
3、自然语言处理：文本分类

1.5.2 算法思想：

寻找到一个超平面使样本分成两类，并且间隔最大。
SVM 采用核函数（Kernel Function）将低维数据映射到高维空间，选用适当的核函数，就能得到高维空间的分割平面，较好地将数据集划分为两部分。
有些数据集在低维的空间中无法使用超平面进行划分，但将其映射到高维空间中，则

能找到一个超平面将不同类的点分割开，如图 5-9 所示。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8nOf9WTv-1644566845689)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417174321303.png)]

1.5.3 计算流程：

核函数选择依据：
1,如果特征的数量大到和样本数量差不多，则选用LR或者线性核的SVM；
2,如果特征的数量小，样本的数量正常，则选用SVM+高斯核函数；
3,如果特征的数量小，而样本的数量很大，则需要手工添加一些特征从而变成第一种情况。

SVM优点:

1、解决小样本下机器学习问题。
2、解决非线性问题。
3、无局部极小值问题。（相对于神经网络等算法）
4、可以很好的处理高维数据集。
5、泛化能力比较强。
SVM缺点:

1、对于核函数的高维映射解释力不强，尤其是径向基函数。
2、对缺失数据敏感。

1.5.4 调包实战

——案例1：

银行投资业务推广预测

某银行客户数据集中包含客户的年龄、孩子个数、收入等 11 个特征项，其中“客户是否接受了银行邮件推荐的个人投资计划”（pep）是相应的分类标签（二分类），前 5 条数据如图 5-10 所示。数据样本共有 600 个，没有缺失数据，保存在 bankpep.csv 文件中。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-GaNDBsR1-1644566845690)(C:\Users\10982\AppData\Roaming\Typora\typora-user-images\image-20210417182623749.png)]

#读入数据
import pandas as pd
filename = 'data/bankpep.csv'
data = pd.read_csv(filename, index_col = 'id')
print( data.iloc[0:5,:])

##数据预处理##
#将最数据中的‘YES’和‘NO'转换成代表分类的整数 1 和 0
seq = ['married', 'car', 'save_act', 'current_act', 'mortgage', 'pep']
for feature in seq :  # 逐个特征进行替换
    data.loc[ data[feature] == 'YES', feature ] =1
    data.loc[ data[feature] == 'NO', feature ] =0
    
#将性别转换为整数1和0
data.loc[ data['sex'] == 'FEMALE', 'sex'] =1
data.loc[ data['sex'] == 'MALE', 'sex'] =0
print(data[0:5])

#将离散特征数据进行独热编码，转换为dummies矩阵
dumm_reg = pd.get_dummies( data['region'], prefix='region' )
print("\nregion的二元矩阵：\n",dumm_reg[0:5])
dumm_child = pd.get_dummies( data['children'], prefix='children' )
print("\nchild的二元矩阵：\n",dumm_child[0:5])

#删除dataframe中原来的两列后再 jion dummies
df1 = data.drop(['region','children'], axis = 1)
#print( df1[0:5])
df2 = df1.join([dumm_reg,dumm_child], how='outer')
print( df2[0:2])

#准备训练输入变量
X = df2.drop(['pep'], axis=1).values.astype(float)
#X = df2.iloc[:,:-1].values.astype(float)
y = df2['pep'].values.astype(int)

支持向量机算法使用sklearn.svm 模块中的SVC方法。常用的参数如下：

C：默认为1.0，是对于错误的惩罚项。
kernel：指定算法的核函数，默认为’rbf’，常用的有**‘linear’，‘poly’，‘rbf’，**‘sigmoid’，‘precomputed’。
degree：多项式核函数的次数（‘poly’），默认为3。其他核函数会将其忽略。
gamma：‘rbf’，‘poly’和’sigmoid’的核系数。如果gamma是’auto’，那么将使用1 / n_features。

这里的数据较小，使用高斯核函数很容易过拟合：

核函数的选择：

当特征很多，样例很少的时候（n很大，m很小）,使用核函数容易过拟合，此时经常选择线性核函数。

在使用核函数之前，最好将特征缩放到相同的范围内。否则训练的效果会很差。

n代表特征数量，m代表样本数量
如果n相对m大很多，建议使用逻辑回归或者svm线性核。否则容易过拟合

如果n很小，m比它大，但是大的不是特别多(1000比10000这种)，建议使用高斯核
如果m相对n大很多，建议创造一些新特征，然后使用逻辑回归或者使用线性核svm。因为此时高斯核运算会很慢。

另外，神经网络可以在大部分场景下都工作的很好，但是训练起来会很慢

————吴恩达

——案例2：

1.6 KNN(K近邻算法)

1.6.1应用场景

‘region’,‘children’], axis = 1)
#print( df1[0:5])
df2 = df1.join([dumm_reg,dumm_child], how=‘outer’)
print( df2[0:2])


```python
#准备训练输入变量
X = df2.drop(['pep'], axis=1).values.astype(float)
#X = df2.iloc[:,:-1].values.astype(float)
y = df2['pep'].values.astype(int)