统计学习导论(ISLR) 第四章分类算法课后习题
统计学习导论(ISLR)
参考资料:
The Elements of Statistical Learning
An Introduction to Statistical Learning
统计学习导论(二):统计学习概述
统计学习导论(三):线性回归
统计学习导论(四):分类
统计学习导论之R语言应用(二):R语言基础
统计学习导论之R语言应用(三):线性回归R语言代码实战
统计学习导论之R语言应用(四):分类算法R语言代码实战
统计学习导论(ISLR)第四章课后习题
文章目录
- 统计学习导论(ISLR)
- 4.分类问题课后习题
-
- 4.13
-
- 4.13.a 制作一些Weekly数据的数字和图形摘要。有什么发现?
- 4.13.b
- 4.13.c
- 4.13.d
- 4.13.e
- 4.13.f
- 4.13.g
- 4.13.h
- 4.13.i
- 4.14 使用Auto数据集,预测汽油里程是高还是低
-
- a.生成一个新的二元变量mpg01,如果mpg>mpg的中位数,则取值为1,否则取值为0
- b.进行探索性数据分析,观察那些变量和mpg01有关
- c.将数据集分为训练集和测试集
- d. LDA
- e.QDA
- f.logistic regression
- g.KNN
- 4.15 函数编写
-
- a
- b 编写一个函数使得其能返回指定次幂
- c 对power2()测试
- d 编写一个函数,使得指定次幂的结果传给一个变量result
- e 使用power3()函数,使得其返回x和x平方的散点图,运用d中的结果
- f 编写一个函数,画出x和x三次方的图
- 4.16 使用波士顿数据集,拟合分类模型,以预测给定census的犯罪率是否高于或低于中等水平。使用各种预测变量集合探索逻辑回归、LDA、朴素贝叶斯和KNN模型。
-
- logistic回归
- lda
- KNN
4.分类问题课后习题
4.13
这个问题使用Weekly数据集,它是ISLR2软件包的一部分。该数据本质上与本章实战代码的市Smarket数据相似,只是他包含的是从1990年初到2010年底的21年的1089周回报
4.13.a 制作一些Weekly数据的数字和图形摘要。有什么发现?
library(ISLR2)
names(Weekly)
- 'Year'
- 'Lag1'
- 'Lag2'
- 'Lag3'
- 'Lag4'
- 'Lag5'
- 'Volume'
- 'Today'
- 'Direction'
# 描述性统计结果
summary(Weeklyy)
Year Lag1 Lag2 Lag3
Min. :1990 Min. :-18.1950 Min. :-18.1950 Min. :-18.1950
1st Qu.:1995 1st Qu.: -1.1540 1st Qu.: -1.1540 1st Qu.: -1.1580
Median :2000 Median : 0.2410 Median : 0.2410 Median : 0.2410
Mean :2000 Mean : 0.1506 Mean : 0.1511 Mean : 0.1472
3rd Qu.:2005 3rd Qu.: 1.4050 3rd Qu.: 1.4090 3rd Qu.: 1.4090
Max. :2010 Max. : 12.0260 Max. : 12.0260 Max. : 12.0260
Lag4 Lag5 Volume Today
Min. :-18.1950 Min. :-18.1950 Min. :0.08747 Min. :-18.1950
1st Qu.: -1.1580 1st Qu.: -1.1660 1st Qu.:0.33202 1st Qu.: -1.1540
Median : 0.2380 Median : 0.2340 Median :1.00268 Median : 0.2410
Mean : 0.1458 Mean : 0.1399 Mean :1.57462 Mean : 0.1499
3rd Qu.: 1.4090 3rd Qu.: 1.4050 3rd Qu.:2.05373 3rd Qu.: 1.4050
Max. : 12.0260 Max. : 12.0260 Max. :9.32821 Max. : 12.0260
Direction
Down:484
Up :605
# 变量散点图
pairs(Weekly)
# 变量相关系数矩阵
cor(Weekly[,-9])
| Year | Lag1 | Lag2 | Lag3 | Lag4 | Lag5 | Volume | Today | |
|---|---|---|---|---|---|---|---|---|
| Year | 1.00000000 | -0.032289274 | -0.03339001 | -0.03000649 | -0.031127923 | -0.030519101 | 0.84194162 | -0.032459894 |
| Lag1 | -0.03228927 | 1.000000000 | -0.07485305 | 0.05863568 | -0.071273876 | -0.008183096 | -0.06495131 | -0.075031842 |
| Lag2 | -0.03339001 | -0.074853051 | 1.00000000 | -0.07572091 | 0.058381535 | -0.072499482 | -0.08551314 | 0.059166717 |
| Lag3 | -0.03000649 | 0.058635682 | -0.07572091 | 1.00000000 | -0.075395865 | 0.060657175 | -0.06928771 | -0.071243639 |
| Lag4 | -0.03112792 | -0.071273876 | 0.05838153 | -0.07539587 | 1.000000000 | -0.075675027 | -0.06107462 | -0.007825873 |
| Lag5 | -0.03051910 | -0.008183096 | -0.07249948 | 0.06065717 | -0.075675027 | 1.000000000 | -0.05851741 | 0.011012698 |
| Volume | 0.84194162 | -0.064951313 | -0.08551314 | -0.06928771 | -0.061074617 | -0.058517414 | 1.00000000 | -0.033077783 |
| Today | -0.03245989 | -0.075031842 | 0.05916672 | -0.07124364 | -0.007825873 | 0.011012698 | -0.03307778 | 1.000000000 |
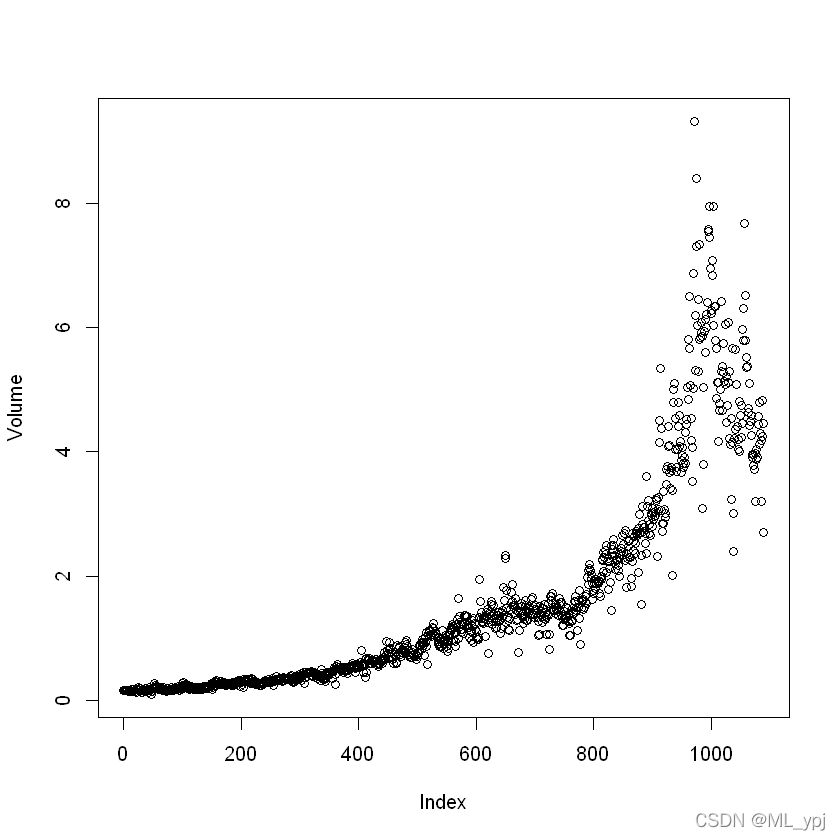
从上表来看,当期回报与之前的回报似乎没有什么相关性。只有年份和数量具有正相关。
说明随着年份增加,股票交易数量会增加
attach(Weekly)
plot(Volume)
The following objects are masked from Weekly (pos = 3):
Direction, Lag1, Lag2, Lag3, Lag4, Lag5, Today, Volume, Year
The following objects are masked from Weekly (pos = 4):
Direction, Lag1, Lag2, Lag3, Lag4, Lag5, Today, Volume, Year
The following objects are masked from Weekly (pos = 5):
Direction, Lag1, Lag2, Lag3, Lag4, Lag5, Today, Volume, Year
4.13.b
使用完整的数据集进行逻辑回归,direction作为响应变量,五个滞后变量加上volume作为预测变量。分析结果,哪些预测变量在统计学上具有显著性?
glm.fit <- glm(
Direction ~ Lag1+Lag2+Lag3+Lag4+Lag5+Volume,
data = Weekly, family = binomial)
summary(glm.fit)
Call:
glm(formula = Direction ~ Lag1 + Lag2 + Lag3 + Lag4 + Lag5 +
Volume, family = binomial, data = Weekly)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.6949 -1.2565 0.9913 1.0849 1.4579
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.26686 0.08593 3.106 0.0019 **
Lag1 -0.04127 0.02641 -1.563 0.1181
Lag2 0.05844 0.02686 2.175 0.0296 *
Lag3 -0.01606 0.02666 -0.602 0.5469
Lag4 -0.02779 0.02646 -1.050 0.2937
Lag5 -0.01447 0.02638 -0.549 0.5833
Volume -0.02274 0.03690 -0.616 0.5377
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1496.2 on 1088 degrees of freedom
Residual deviance: 1486.4 on 1082 degrees of freedom
AIC: 1500.4
Number of Fisher Scoring iterations: 4
从上述结果发现,变量Lag2通过了显著性检验,且系数为正,说明当滞后两期的回报率上升时,当期回报率也会上升
4.13.c
计算混淆矩阵中预测的总准确率。解释混淆矩阵告诉你的逻辑回归错误类型。
# 首先预测结果,指定type='response',返回的是为1的概率
glm.probs <- predict(glm.fit, type='response')
# 将结果创建为down和up的列表
pred <- rep('Down', 1089)
pred[glm.probs>.5] = 'Up'
# table得到混淆矩阵
table(pred, Direction)
Direction
pred Down Up
Down 54 48
Up 430 557
# 计算总的正确率
mean(pred == Direction)
0.561065197428834
我们得出总正确率是0.56,其中在up类中,预测的正确率较高,但是在down类中,只有54/430+54=0.11的概率正确
4.13.d
现在,使用1990年至2008年的训练数据拟合逻辑回归模型,2009-2010年的数据为测试集。Lag2是唯一的预测变量。
通过拟合的模型对测试集进行检验
# 划分数据集
train <- Weekly[Weekly['Year'] < 2009,]
test <- Weekly[Weekly['Year'] >= 2009,]
dim(train)
dim(test)
- 985
- 9
- 104
- 9
glm.fit <- glm(Direction~Lag2,
data=train,family=binomial
)
summary(glm.fit)
Call:
glm(formula = Direction ~ Lag2, family = binomial, data = train)
Deviance Residuals:
Min 1Q Median 3Q Max
-1.536 -1.264 1.021 1.091 1.368
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 0.20326 0.06428 3.162 0.00157 **
Lag2 0.05810 0.02870 2.024 0.04298 *
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1354.7 on 984 degrees of freedom
Residual deviance: 1350.5 on 983 degrees of freedom
AIC: 1354.5
Number of Fisher Scoring iterations: 4
glm.prob <- predict(glm.fit, test, type = 'response')
glm.pred <- rep('Down', 104)
glm.pred[glm.prob>0.5] <- 'Up'
table (glm.pred, test$Direction)
glm.pred Down Up
Down 9 5
Up 34 56
mean(glm.pred == test$Direction)
0.625
4.13.e
使用lda拟合
library(MASS)
lda.fit <- lda(Direction~Lag2,
data=train)
lda.pred <- predict(lda.fit, test, type = 'response')
table(lda.pred$class, test$Direction)
Down Up
Down 9 5
Up 34 56
发现结果和logistic回归相同
4.13.f
使用QDA拟合
qda.fit = qda(Direction ~ Lag2, data = train)
qda.class = predict(qda.fit, test)$class
table(qda.class, test$Direction)
qda.class Down Up
Down 0 0
Up 43 61
mean(qda.class == test$Direction)
0.586538461538462
4.13.g
使用KNN(K=1)拟合
使用KNN首先要输入四个参数:
- 训练集的输入变量矩阵
- 测试集的输入变量矩阵
- 测试集的输出变量
- k值
# 导入相关库
library(class)
#定义相关矩阵
train.X = as.matrix(train['Lag2'])
test.X = as.matrix(test['Lag2'])
train.Direction = train$Direction
set.seed(1)
knn.pred = knn(train.X, test.X, train.Direction, k = 1)
table(knn.pred, test$Direction)
knn.pred Down Up
Down 21 30
Up 22 31
mean(knn.pred == test$Direction)
0.5
4.13.h
使用朴素贝叶斯拟合
library(e1071)
nb.fit <- naiveBayes(Direction ~ Lag2, data = train)
nb.fit
Naive Bayes Classifier for Discrete Predictors
Call:
naiveBayes.default(x = X, y = Y, laplace = laplace)
A-priori probabilities:
Y
Down Up
0.4477157 0.5522843
Conditional probabilities:
Lag2
Y [,1] [,2]
Down -0.03568254 2.199504
Up 0.26036581 2.317485
nb.class <- predict(nb.fit, test)
table(nb.class, test$Direction)
nb.class Down Up
Down 0 0
Up 43 61
4.13.i
哪一种对这批数据拟合效果最好
逻辑回归和LDA测试误差最小。
4.14 使用Auto数据集,预测汽油里程是高还是低
dim(Auto)
- 392
- 9
a.生成一个新的二元变量mpg01,如果mpg>mpg的中位数,则取值为1,否则取值为0
me_mpg <- median(Auto$mpg)
mpg01 <- rep(0,392)
mpg01[Auto$mpg>me_mpg]<-1
# 连接数据
Auto = data.frame(Auto, mpg01)
b.进行探索性数据分析,观察那些变量和mpg01有关
pairs(Auto)
summary(Auto)
mpg cylinders displacement horsepower weight
Min. : 9.00 Min. :3.000 Min. : 68.0 Min. : 46.0 Min. :1613
1st Qu.:17.00 1st Qu.:4.000 1st Qu.:105.0 1st Qu.: 75.0 1st Qu.:2225
Median :22.75 Median :4.000 Median :151.0 Median : 93.5 Median :2804
Mean :23.45 Mean :5.472 Mean :194.4 Mean :104.5 Mean :2978
3rd Qu.:29.00 3rd Qu.:8.000 3rd Qu.:275.8 3rd Qu.:126.0 3rd Qu.:3615
Max. :46.60 Max. :8.000 Max. :455.0 Max. :230.0 Max. :5140
acceleration year origin name
Min. : 8.00 Min. :70.00 Min. :1.000 amc matador : 5
1st Qu.:13.78 1st Qu.:73.00 1st Qu.:1.000 ford pinto : 5
Median :15.50 Median :76.00 Median :1.000 toyota corolla : 5
Mean :15.54 Mean :75.98 Mean :1.577 amc gremlin : 4
3rd Qu.:17.02 3rd Qu.:79.00 3rd Qu.:2.000 amc hornet : 4
Max. :24.80 Max. :82.00 Max. :3.000 chevrolet chevette: 4
(Other) :365
mpg01
Min. :0.0
1st Qu.:0.0
Median :0.5
Mean :0.5
3rd Qu.:1.0
Max. :1.0
cor(Auto[,-9])
| mpg | cylinders | displacement | horsepower | weight | acceleration | year | origin | mpg01 | |
|---|---|---|---|---|---|---|---|---|---|
| mpg | 1.0000000 | -0.7776175 | -0.8051269 | -0.7784268 | -0.8322442 | 0.4233285 | 0.5805410 | 0.5652088 | 0.8369392 |
| cylinders | -0.7776175 | 1.0000000 | 0.9508233 | 0.8429834 | 0.8975273 | -0.5046834 | -0.3456474 | -0.5689316 | -0.7591939 |
| displacement | -0.8051269 | 0.9508233 | 1.0000000 | 0.8972570 | 0.9329944 | -0.5438005 | -0.3698552 | -0.6145351 | -0.7534766 |
| horsepower | -0.7784268 | 0.8429834 | 0.8972570 | 1.0000000 | 0.8645377 | -0.6891955 | -0.4163615 | -0.4551715 | -0.6670526 |
| weight | -0.8322442 | 0.8975273 | 0.9329944 | 0.8645377 | 1.0000000 | -0.4168392 | -0.3091199 | -0.5850054 | -0.7577566 |
| acceleration | 0.4233285 | -0.5046834 | -0.5438005 | -0.6891955 | -0.4168392 | 1.0000000 | 0.2903161 | 0.2127458 | 0.3468215 |
| year | 0.5805410 | -0.3456474 | -0.3698552 | -0.4163615 | -0.3091199 | 0.2903161 | 1.0000000 | 0.1815277 | 0.4299042 |
| origin | 0.5652088 | -0.5689316 | -0.6145351 | -0.4551715 | -0.5850054 | 0.2127458 | 0.1815277 | 1.0000000 | 0.5136984 |
| mpg01 | 0.8369392 | -0.7591939 | -0.7534766 | -0.6670526 | -0.7577566 | 0.3468215 | 0.4299042 | 0.5136984 | 1.0000000 |
可以发现与cylinders, weight, displacement, horsepower呈现较强的负相关
c.将数据集分为训练集和测试集
由于这里没有明确的指明数据集和训练集,我这里选择year<80的作为训练集
train <- Auto[Auto$year<80,]
test <- Auto[Auto$year>=80,]
d. LDA
使用LDA拟合模型
# LDA
library(MASS)
lda.fit <-lda(mpg01 ~ cylinders + weight + displacement + horsepower, data = train)
lda.pred <- predict(lda.fit, test)
mean(lda.pred$class != test$mpg01)
0.129411764705882
e.QDA
使用qda拟合模型
library(MASS)
qda.fit <- qda(mpg01 ~ cylinders + weight + displacement + horsepower, data = train)
qda.pred <- predict(qda.fit, test)
mean(qda.pred$class != test$mpg01)
0.129411764705882
f.logistic regression
使用logistic regression拟合模型
glm.fit <- glm(mpg01 ~ cylinders + weight + displacement + horsepower, data = train,family = binomial)
glm.prob <- predict(glm.fit, test)
glm.pred <- rep(0,length(glm.prob))
glm.pred[glm.prob>.5] <- 1
mean(glm.pred!= test$mpg01)
0.270588235294118
g.KNN
使用KNN比较模型,并比较不同K值的效果
library(class)
train.X <- cbind(train$cylinders, train$weight, train$displacement, train$horsepower)
test.X <- cbind(test$cylinders, test$weight, test$displacement, test$horsepower)
set.seed(1)
# KNN(k=1)
knn.pred <- knn(train.X, test.X, train$mpg01, k = 1)
mean(knn.pred != test$mpg01)
0.2
# KNN(k=10)
knn.pred <- knn(train.X, test.X, train$mpg01, k = 10)
mean(knn.pred != test$mpg01)
0.223529411764706
# KNN(k=100)
knn.pred <- knn(train.X, test.X, train$mpg01, k = 100)
mean(knn.pred != test$mpg01)
0.235294117647059
在本数据集中,k=1优于k=10优于k=100
4.15 函数编写
a
编写power函数,使得其返回2^3的值
power = function(){
2^3
}
print(power())
[1] 8
b 编写一个函数使得其能返回指定次幂
power2 = function(x,a){
x^a
}
print(power2(3,8))
[1] 6561
c 对power2()测试
power2(8,17)
2251799813685248
power(131,3)
2248091
d 编写一个函数,使得指定次幂的结果传给一个变量result
power3 = function(x,a){
result = x^a
return(result)
}
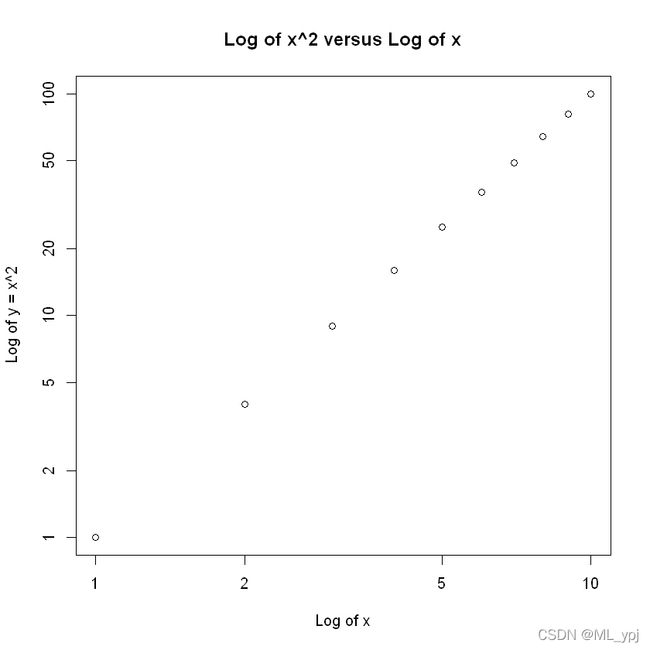
e 使用power3()函数,使得其返回x和x平方的散点图,运用d中的结果
x = 1:10
plot(x, power3(x, 2), log = "xy", ylab = "Log of y = x^2", xlab = "Log of x",
main = "Log of x^2 versus Log of x")
f 编写一个函数,画出x和x三次方的图
PlotPower = function(x, a) {
plot(x, power3(x, a))
}
PlotPower(1:10, 3)
4.16 使用波士顿数据集,拟合分类模型,以预测给定census的犯罪率是否高于或低于中等水平。使用各种预测变量集合探索逻辑回归、LDA、朴素贝叶斯和KNN模型。
首先我们和Auto数据集问题一样,首先要生成一个二元变量,判断犯罪率高于或低于中等犯罪率
# 导入相关库
library(MASS)
summary(Boston)
crim zn indus chas
Min. : 0.00632 Min. : 0.00 Min. : 0.46 Min. :0.00000
1st Qu.: 0.08205 1st Qu.: 0.00 1st Qu.: 5.19 1st Qu.:0.00000
Median : 0.25651 Median : 0.00 Median : 9.69 Median :0.00000
Mean : 3.61352 Mean : 11.36 Mean :11.14 Mean :0.06917
3rd Qu.: 3.67708 3rd Qu.: 12.50 3rd Qu.:18.10 3rd Qu.:0.00000
Max. :88.97620 Max. :100.00 Max. :27.74 Max. :1.00000
nox rm age dis
Min. :0.3850 Min. :3.561 Min. : 2.90 Min. : 1.130
1st Qu.:0.4490 1st Qu.:5.886 1st Qu.: 45.02 1st Qu.: 2.100
Median :0.5380 Median :6.208 Median : 77.50 Median : 3.207
Mean :0.5547 Mean :6.285 Mean : 68.57 Mean : 3.795
3rd Qu.:0.6240 3rd Qu.:6.623 3rd Qu.: 94.08 3rd Qu.: 5.188
Max. :0.8710 Max. :8.780 Max. :100.00 Max. :12.127
rad tax ptratio black
Min. : 1.000 Min. :187.0 Min. :12.60 Min. : 0.32
1st Qu.: 4.000 1st Qu.:279.0 1st Qu.:17.40 1st Qu.:375.38
Median : 5.000 Median :330.0 Median :19.05 Median :391.44
Mean : 9.549 Mean :408.2 Mean :18.46 Mean :356.67
3rd Qu.:24.000 3rd Qu.:666.0 3rd Qu.:20.20 3rd Qu.:396.23
Max. :24.000 Max. :711.0 Max. :22.00 Max. :396.90
lstat medv
Min. : 1.73 Min. : 5.00
1st Qu.: 6.95 1st Qu.:17.02
Median :11.36 Median :21.20
Mean :12.65 Mean :22.53
3rd Qu.:16.95 3rd Qu.:25.00
Max. :37.97 Max. :50.00
# 修改数据集
attach(Boston)
crim01 <- rep(0, length(crim))
crim01[crim>median(crim)] <- 1
Boston <- data.frame(Boston, crim01)
The following objects are masked from Boston (pos = 3):
age, black, chas, crim, dis, indus, lstat, medv, nox, ptratio, rad,
rm, tax, zn
# 探索性数据分析
# 变量散点图
pairs(Boston)
# 变量之间相关系数
cor(Boston)
| crim | zn | indus | chas | nox | rm | age | dis | rad | tax | ptratio | black | lstat | medv | crim01 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| crim | 1.00000000 | -0.20046922 | 0.40658341 | -0.055891582 | 0.42097171 | -0.21924670 | 0.35273425 | -0.37967009 | 0.625505145 | 0.58276431 | 0.2899456 | -0.38506394 | 0.4556215 | -0.3883046 | 0.40939545 |
| zn | -0.20046922 | 1.00000000 | -0.53382819 | -0.042696719 | -0.51660371 | 0.31199059 | -0.56953734 | 0.66440822 | -0.311947826 | -0.31456332 | -0.3916785 | 0.17552032 | -0.4129946 | 0.3604453 | -0.43615103 |
| indus | 0.40658341 | -0.53382819 | 1.00000000 | 0.062938027 | 0.76365145 | -0.39167585 | 0.64477851 | -0.70802699 | 0.595129275 | 0.72076018 | 0.3832476 | -0.35697654 | 0.6037997 | -0.4837252 | 0.60326017 |
| chas | -0.05589158 | -0.04269672 | 0.06293803 | 1.000000000 | 0.09120281 | 0.09125123 | 0.08651777 | -0.09917578 | -0.007368241 | -0.03558652 | -0.1215152 | 0.04878848 | -0.0539293 | 0.1752602 | 0.07009677 |
| nox | 0.42097171 | -0.51660371 | 0.76365145 | 0.091202807 | 1.00000000 | -0.30218819 | 0.73147010 | -0.76923011 | 0.611440563 | 0.66802320 | 0.1889327 | -0.38005064 | 0.5908789 | -0.4273208 | 0.72323480 |
| rm | -0.21924670 | 0.31199059 | -0.39167585 | 0.091251225 | -0.30218819 | 1.00000000 | -0.24026493 | 0.20524621 | -0.209846668 | -0.29204783 | -0.3555015 | 0.12806864 | -0.6138083 | 0.6953599 | -0.15637178 |
| age | 0.35273425 | -0.56953734 | 0.64477851 | 0.086517774 | 0.73147010 | -0.24026493 | 1.00000000 | -0.74788054 | 0.456022452 | 0.50645559 | 0.2615150 | -0.27353398 | 0.6023385 | -0.3769546 | 0.61393992 |
| dis | -0.37967009 | 0.66440822 | -0.70802699 | -0.099175780 | -0.76923011 | 0.20524621 | -0.74788054 | 1.00000000 | -0.494587930 | -0.53443158 | -0.2324705 | 0.29151167 | -0.4969958 | 0.2499287 | -0.61634164 |
| rad | 0.62550515 | -0.31194783 | 0.59512927 | -0.007368241 | 0.61144056 | -0.20984667 | 0.45602245 | -0.49458793 | 1.000000000 | 0.91022819 | 0.4647412 | -0.44441282 | 0.4886763 | -0.3816262 | 0.61978625 |
| tax | 0.58276431 | -0.31456332 | 0.72076018 | -0.035586518 | 0.66802320 | -0.29204783 | 0.50645559 | -0.53443158 | 0.910228189 | 1.00000000 | 0.4608530 | -0.44180801 | 0.5439934 | -0.4685359 | 0.60874128 |
| ptratio | 0.28994558 | -0.39167855 | 0.38324756 | -0.121515174 | 0.18893268 | -0.35550149 | 0.26151501 | -0.23247054 | 0.464741179 | 0.46085304 | 1.0000000 | -0.17738330 | 0.3740443 | -0.5077867 | 0.25356836 |
| black | -0.38506394 | 0.17552032 | -0.35697654 | 0.048788485 | -0.38005064 | 0.12806864 | -0.27353398 | 0.29151167 | -0.444412816 | -0.44180801 | -0.1773833 | 1.00000000 | -0.3660869 | 0.3334608 | -0.35121093 |
| lstat | 0.45562148 | -0.41299457 | 0.60379972 | -0.053929298 | 0.59087892 | -0.61380827 | 0.60233853 | -0.49699583 | 0.488676335 | 0.54399341 | 0.3740443 | -0.36608690 | 1.0000000 | -0.7376627 | 0.45326273 |
| medv | -0.38830461 | 0.36044534 | -0.48372516 | 0.175260177 | -0.42732077 | 0.69535995 | -0.37695457 | 0.24992873 | -0.381626231 | -0.46853593 | -0.5077867 | 0.33346082 | -0.7376627 | 1.0000000 | -0.26301673 |
| crim01 | 0.40939545 | -0.43615103 | 0.60326017 | 0.070096774 | 0.72323480 | -0.15637178 | 0.61393992 | -0.61634164 | 0.619786249 | 0.60874128 | 0.2535684 | -0.35121093 | 0.4532627 | -0.2630167 | 1.00000000 |
发现chas、rm与crim01相关系数较小,下面划分数据集为训练集和测试集,本文粗略的将训练集和训练集按2:1来分
(实际应用时应该先随机打乱,再进行划分。并且如果数据足够大的话,最好分为训练集、验证集和测试集,
在训练集上拟合多个模型,验证集选择模型,测试集上评估模型)
train <- 1:(dim(Boston)[1]/3*2)
test <- 1:(dim(Boston)[1]/3)
Boston.train <- Boston[train,]
Boston.test <- Boston[test,]
crim01.test <- Boston.test$crim01
logistic回归
# logistic regression
glm.fit <- glm(crim01~.-chas-rm-crim01-crim, data = Boston.train, family = binomial)
glm.probs <- predict(glm.fit, Boston.test, type = 'response')
glm.pred <- rep(0,length(glm.probs))
glm.pred[glm.probs>.5] <- 1
mean(glm.pred == crim01.test)
0.93452380952381
lda
lda.fit <- lda(crim01~.-chas-rm-crim01-crim, data = Boston.train)
lda.pred <- predict(lda.fit, Boston.test)
mean(lda.pred$class == crim01.test)
0.857142857142857
此时正确率下降到85.7%,下面我们分别使用KNN来拟合模型
KNN
train.X = cbind(zn, indus, chas, nox, rm, age, dis, rad, tax, ptratio, black,
lstat, medv)[train, ]
test.X = cbind(zn, indus, chas, nox, rm, age, dis, rad, tax, ptratio, black,
lstat, medv)[test, ]
train.Y <- Boston.train$crim01
# k=1
knn.pred <- knn(train.X, test.X,train.Y, k=1)
mean(knn.pred == crim01.test)
1
# KNN(k=10)
knn.pred = knn(train.X, test.X, train.Y, k = 10)
mean(knn.pred == crime01.test)
0.922619047619048