深蓝-视觉slam-第三讲学习笔记
第三讲 李群和李代数
1.群
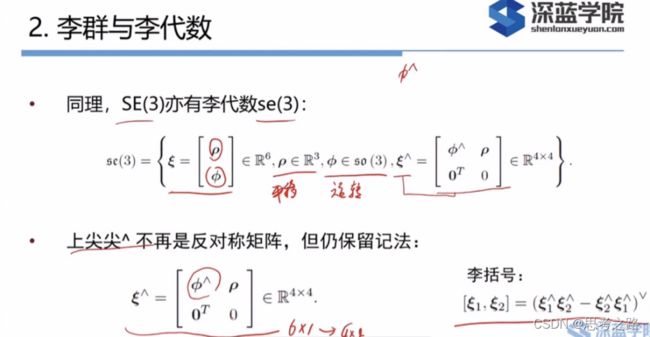
2.李群和李代数
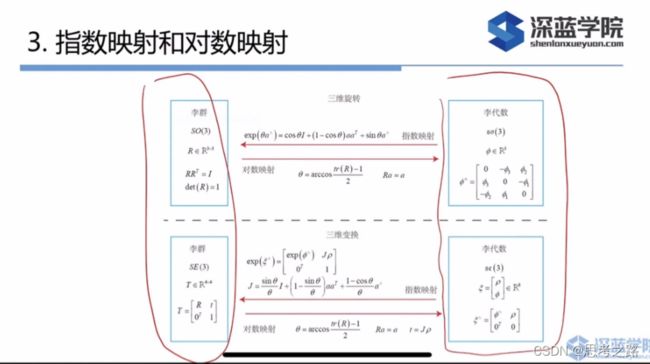
3.指数映射与对数映射
4.求导与扰动模型
5.实践:Sophus
引入李群和李代数的原因是为了估计相机的运动,相机在时间上的连续运动构成李群,因为在状态估计中需要估计李群的性质,需要引入李群和李代数的概念。
旋转矩阵自身是有约束的,作为优化变量时,会引入额外的约束,使得优化变得困难。通过李群——李代数间的转换关系,我们希望把位姿估计变成没有约束的优化问题,简化求解方式。

xk的描述可以通过一个旋转矩阵(R)+平移向量(t) 或者**变换矩阵 (T)**来描述;
如果已经知道了一些输入和观测值,如何求出x,y:状态估计问题, 由初始值迭代去计算更好的估计。
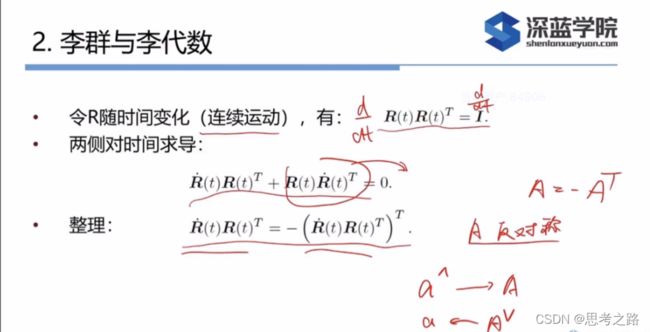
(f(R+ Δ \Delta ΔR) - f(R))/ dR 导数的定义:f(R+ Δ \Delta ΔR),旋转矩阵是个矩阵,但R的上面是定义不出加法的,两个旋转矩阵相加已经不再是一个旋转矩阵了,不属于SO3(特殊正交群),不满足正交和行列式为1的条件了,这个集合上没有一个良好定义的加法。当没有加法的时候,如何定义自己的导数,不能用通用的处理向量或向量的方式去处理旋转矩阵和变换矩阵,引入数学工具:李群和李代数。

R,T对加法不封闭:对于任意两个旋转矩阵R1,R2,按照矩阵加法的定义,和不再是一个旋转矩阵:
R1 + R2 ∉ \notin ∈/ SO(3), T1 + T2 ∉ \notin ∈/ SE(3)
R,T对乘法是封闭的:
R1 * R2 ∈ \in ∈ SO(3), T1 * T2 ∈ \in ∈ SE(3)

常见的群包括:整数的加法(Z,+),去掉0后有理数的乘法(幺元为1)(Q\0, .)
群结构保证了在群上的运算具有良好的性质。


流形:高维空间中的低维连续的东西,例如曲面是三维空间中两维的东西,旋转矩阵R是九维空间中三维的东西(三维的流形),从高维看维度低,但从局部看起来像R3(三维的东西)

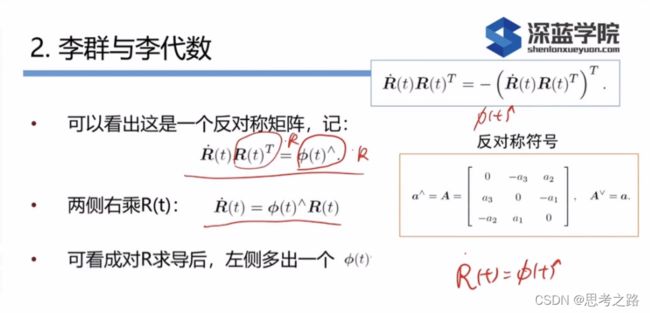



由于 ∅ \emptyset ∅是个三维向量,我们可以定义它的模长和方向,分别记作 θ \theta θ和a,于是有 ∅ \emptyset ∅ = θ \theta θa.这里a是一个长度为1的方向向量。
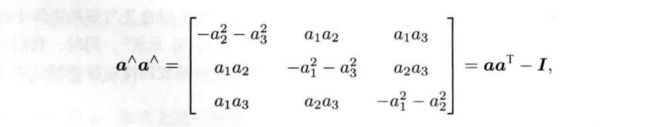
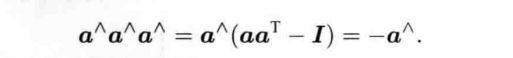

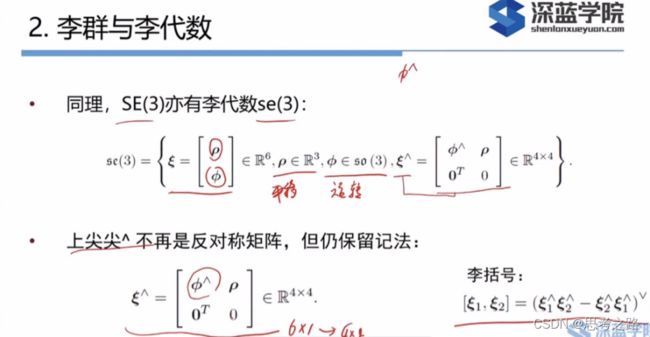
由泰勒展开后的结果可以看出:so(3)实际上就是由旋转向量组成的空间,指数映射即罗德里格斯公式。

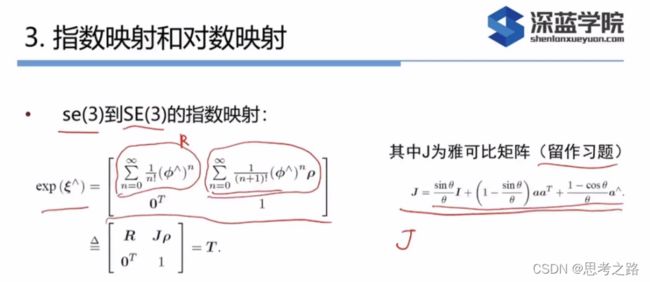
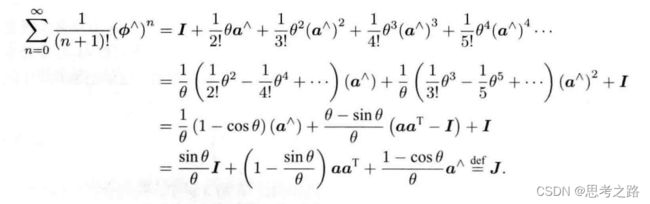
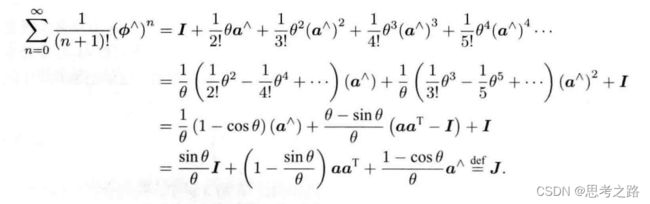
使用李代数的一大动机是进行优化,而在优化的过程中导数是非常必要的信息。

ln(exp(A) + exp(B)) = A + B?该式在矩阵中不成立。

BCH公式告诉我们,当处理两个矩阵指数之积时,他们会产生一些由李括号组成的余项。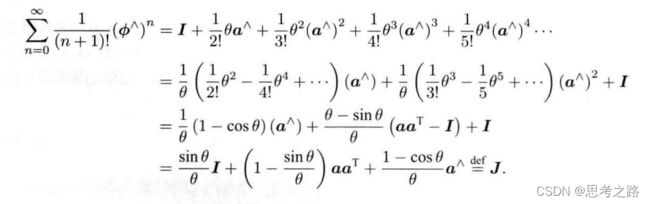


上式告诉我们:当对一个旋转矩阵R2(李代数 ∅ \emptyset ∅ 2)左乘一个微小的旋转矩阵R1时,可以近似的看作,在原有李代数的 ∅ \emptyset ∅ 2 的基础上加了一项![]()
第二个近似描述了右乘一个微小位移的情况。于是,李代数在BCH近似下分成了左乘和右乘的模型。

![]()
在SLAM中,我们要估计一个相机的位置和姿态,该位姿由SO(3)上的旋转矩阵或SE(3)上的变换矩阵来描述。不妨设某个时机器人的位姿为T,它观察到了一个ie世界坐标系位于p的点,产生了一个观测数据z。那么坐标变换关系:z = Tp + w 其中w时随即噪声。由于它的存在,z往往不能精确的满足z=Tp的关系。所以我们通常会计算理想的观测与实际数据的误差:
e = z -Tp ,若共有N个这样的路标点和观测,于是就有N个上式。那么对机器人进行位姿估计,就是寻找最优的T,使得误差最小:
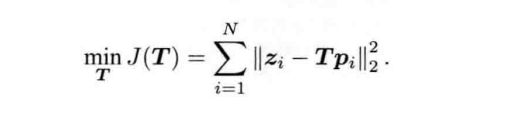




实践
github上下载Sophus库,然后进行编译,无需安装
(1).下面时Sophus库中的Sophus库中的SO(3) 和SE(3)的运算:
#includecmake_minimum_required(VERSION 3.4)
project(useSophus)
set(CMAKE_BUILD_TYPE "Release")
find_package(Sophus REQUIRED)
include_directories(${Sophus_INCLUDE_DIRS})
include_directories("/usr/include/eigen3")
add_executable(useSophus useSophus.cpp)
#target_link_libraries(useSophus Sophus::Sophus)
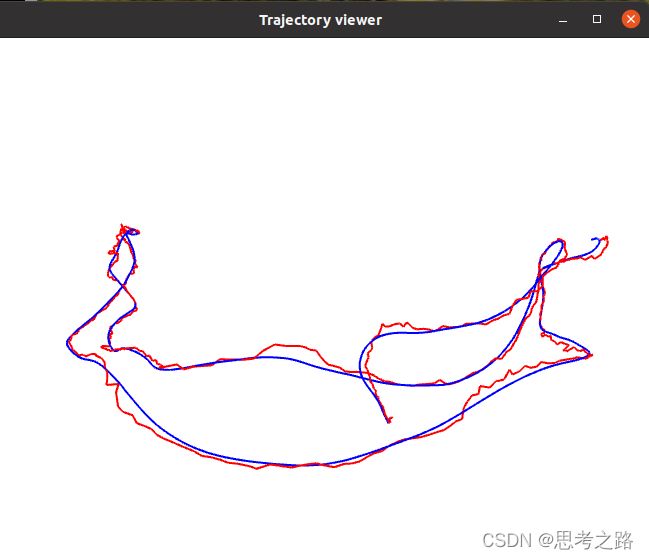
(2).评估轨迹的误差
估计轨迹可以由待评价的算法计算所的,真实轨迹需要更高精度的系统获取。
估计轨迹Testi,i 和真实轨迹Tgt,i,其中i=1,…,N,那么通过一些定义好的误差指标,我们就可以描述它们之间的差别。
绝对轨迹i误差 (Absolute Trajectory Error, ATE),
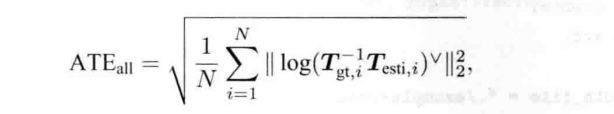
这是每个位姿李代数的均方根误差(Root-Mean-Squared Error,RMSE),这种误差可以刻画两条轨迹的旋转和平移误差。
绝对平移误差(Average Translation Error):
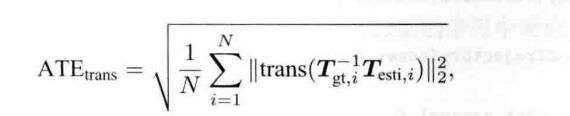
其中trans表示括号内部便来嗯的平移部分。因为从整条轨迹上看,轨迹出现误差后,随后的轨迹在平移上也会出现误差,所以两种指标的实际中都适用。
相对位姿误差(Relative Pose Error,RPE):考虑i时刻到i+ Δ \Delta Δt时刻的运动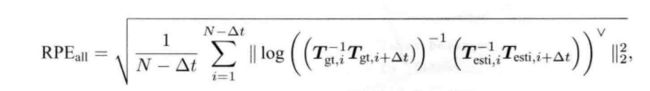
同样也可只取平移部分:

下面利用Sophus库,来演示绝对轨迹误差的计算
#include cmake_minimum_required(VERSION 3.4)
project(useSophus)
set(CMAKE_BUILD_TYPE "Release")
find_package(Sophus REQUIRED)
include_directories(${Sophus_INCLUDE_DIRS})
find_package(Pangolin REQUIRED)
include_directories(${Pangolin_INCLUDE_DIRS})
include_directories("/usr/include/eigen3")
add_executable(trajectoryError trajectoryError.cpp)
#add_executable(useSophus useSophus.cpp)
target_link_libraries(trajectoryError ${Pangolin_LIBRARIES})
target_link_libraries(trajectoryError ${Sophus_LIBRARIES})
*扩展知识
单目视觉中使用的相似变换群Sim(3),以及对应的李代数(sim(3))。如果在单目SLAM中使用SE(3)来表示位姿,由于尺度不确定性和尺度漂移,整个SLAM过程中尺度会发生变化,这在SE(3)中并没有体现,因此我们引进相似变换来显示的把这个尺度因子表达出来。
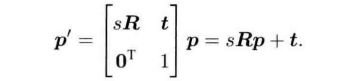
和SO(3),SE(3)一样,相似变换对矩阵乘法也构成群,称为相似变换群(Sim(3)):
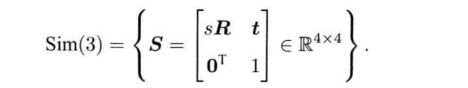
Sim(3)也有对应的李代数,指数映射,对数映射等。李代数sim(3)元素是一个7维向量 ζ \zeta ζ,前6维和se(3)相同,对了一项 σ \sigma σ
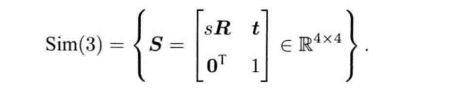
指数映射:
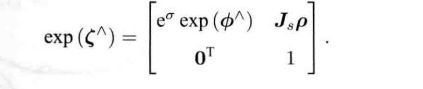
其中Js的形式:
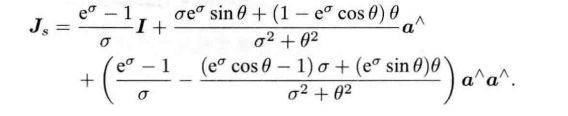
李代数与李群的对应关系为:
![]()
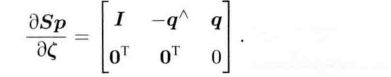
总结:引入李群和李代数,然后通过BCH的线性近似,对位姿进行扰动并求导,为之后的位姿优化打下基础。