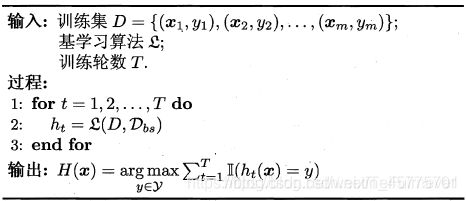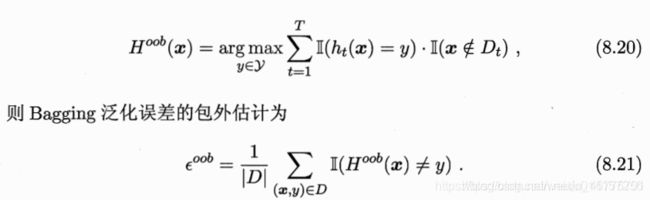《机器学习》周志华--第8章集成学习。笔记+习题

集成学习的目的是： 通过适当的学习方法将弱学习器转化为强学习器
方法要点为：优而不同

8.1个体与集成

1.集成学习概念和一般结构

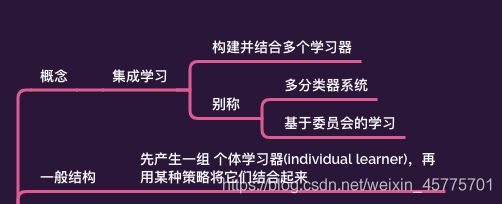
• 集成学习概念

集成学习（多分类器系统/基于委员会的学习）：生成一组个体学习器并将它们结合起来。

• 示意图
  集成学习可得到比单一学习器更好的泛化性能，尤其是弱学习器：泛化性能略大于50％

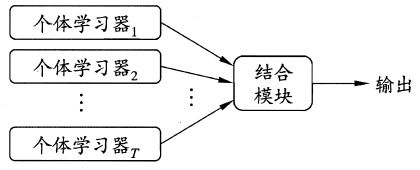
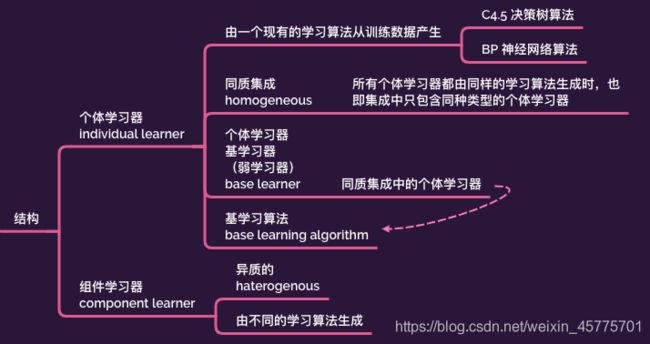
2.结构

3.性能

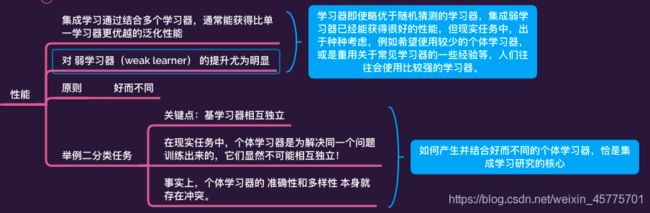
举一个简单的例子：在二分类任务中，假定三个分类器在三个测试样本上的表现如图所示：

通过单一变量法，a表示好而不同的分类器，b表示好但相同的分类器，c表示不好但不同的分类器。

其中 √ 表示分类正确，× 表示分类错误，集成学习的结果通过投票法(voting)产生，即 少数服从多数。
在图(a)中，每个分类器都只有66.6% 的精度，但集成学习却达到了100%；
在图(b)中，三个分类器没有差别，集成之后性能没有提高；
在图© 中，每个分类器的精度都只有33.3%，集成学习的结果变得更糟。
这个简单的例子显示出：要获得好的集成，个体学习器应好而不同。

在分类器的错误率相互独立的前提下集成的错误率：（Hoeffding不等式）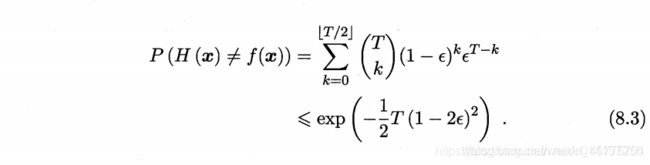
随着个体分类器数目T增大，集成错误率下降。

4.分类

8.2Boosting

主要关注降低偏差，可将弱学习器提升为强学习器的算法

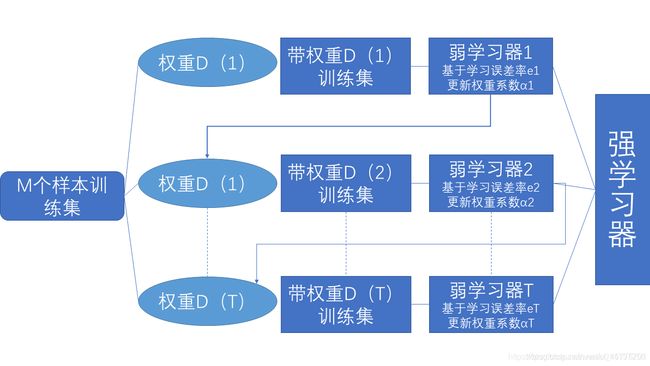
1.工作机制

2.AdaBoosting

详细总结：link.
有两个例子
链接: link.
链接: link.
把第2个例子转过来。

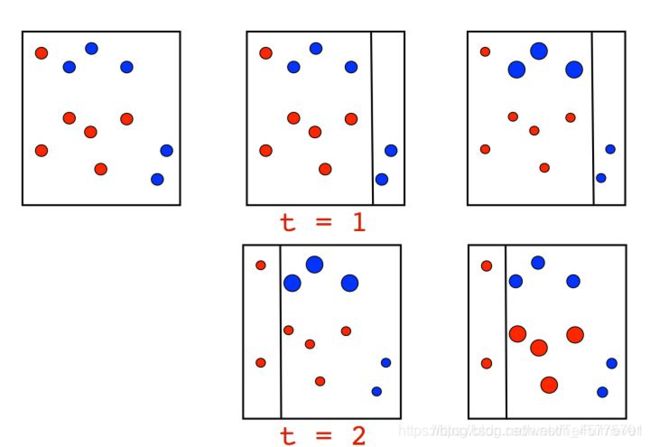
一个二元分类问题，如何划分红球和篮球。显然这个问题用一个线性分类器的话很难取得最好的效果。有没有办法通过组合一系列和正方形平行的线（每条线都相当于一个线性分类器）来获得一个比较好的分类效果呢？
第一步：先矮子里拔将军，选择一条平行于四边且最不坏的线段。下图第一排中间的小图里，直线把图分为左边（红点）和右边（蓝点）两类，被错分的点只有3个，这似乎是能得到的最好的结果了。然后我们想去找第二条线（第二个线性分类器）。如果只是基于现有的这些点的话那么说不定得到的线段还是和之前那条差不多，那多个线段（线性分类器）就没有意义了。所以我们要稍微调整一下某些点在分类结果里的重要性，提升他们的权重。我们在这里提升了那三个被错分的点的权重。
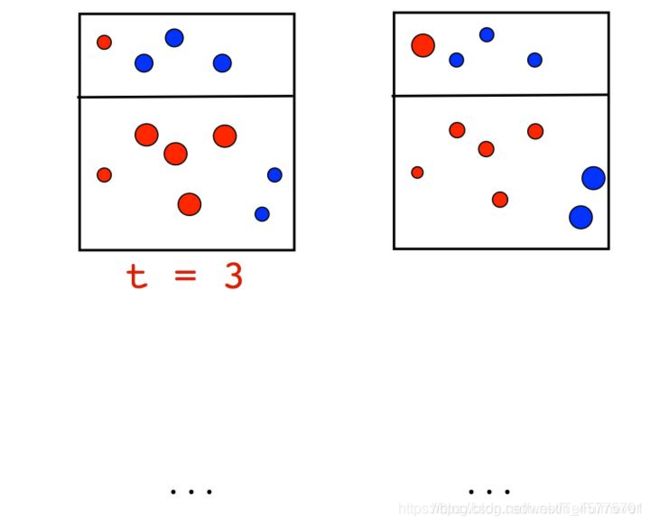
第二步：我们找到了一条新的线段，因为之前提升了把蓝点和蓝点分在一起的重要性，所以这条线段没有选择平行于上下两边把上面4个点（1红3蓝）和下面7个点（5红2蓝）分开，而是选择尽可能多地把蓝点归在一起。然而这次不同的是我们分错的是右边那4个红点，于是我们放大那4个红点，提升他们的权重。
不断重复这一过程。
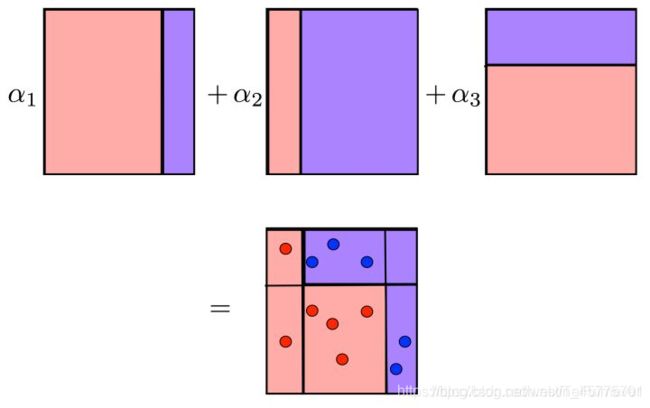
最终我们得到了多个线性分类器，把这些线性分类器的结果做一个线性组合，我们就得到了整个集成模型的结果。每个线性分类器的结果的系数（权重）取决于它的表现，表现越好，权重越高。比如第一条线段的分类错误就优于第二条线段，那么它获得的权重也就会更大。集成模型的效果非常好。

顺带一提，第一条线段的分类正确率是8/11，第二条线段的分类正确率是7/11，第三条线段的分类正确率是8/11，确实要好于随机猜测（以1/2为界）。

3.对基学习器的要求

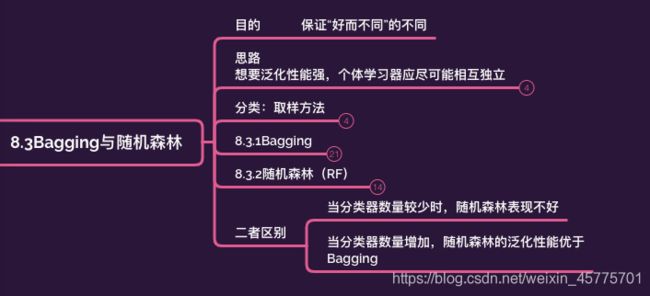
8.3Bagging与随机森林

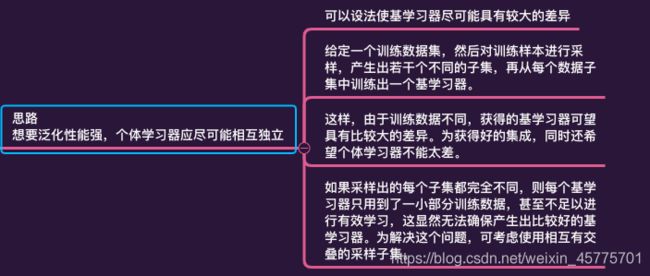
1.思路

2.分类：取样方法

3.Bagging

主要关注降低方差，因此它在不剪枝决策树、神经网络等易受样本扰动的学习器上效用更为明显。

• 流程
  
  Bagging 的算法描述图如下：

• 对预测输出进行结合
  

• 优点

优点：复杂度低，仅比只用基学习算法多了一个采样和投票环节，能直接用于分类、回归，自主采样剩余样本可用于对泛化性能的外包估计↓

4.随机森林

随机森林是Bagging的一个扩展变体


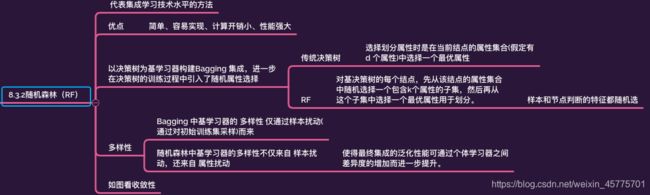
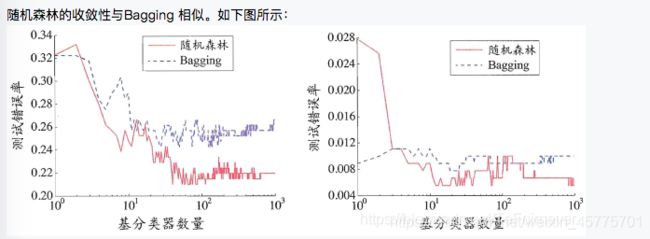
随机森林的起始性能往往相对较差， 特别是在集成中只包含一个基学习器时，这很容易理解，因为通过引入属性扰动，随机森林中个体学习器的性能往往有所降低。然而，随着个体学习器数目的增加，随机森林通常会收敛到更低的泛化误差。值得一提的是，随机森林的训练效率常优于Bagging，因为在个体决策树的构建过程中， Bagging 使用的是 确定型决策树，在选择划分属性时要对结点的所有属性进行考察，而随机森林使用的 随机型决策树 则只需考察一个属性子集。

5.二者区别

8.4结合策略

1.好处

直观示意图如下：

2.平均法

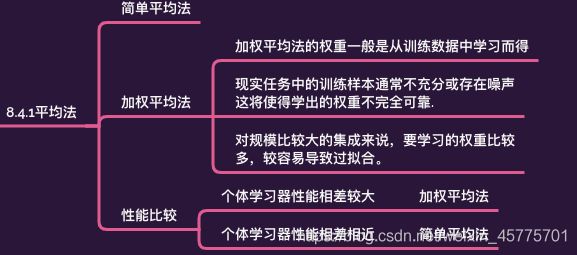
其中 i是个体学习器的权重，一般是从训练数据中习得。在个体学习器性能相差较大时宜使用加权平均法，而在个体学习器性能相近时宜使用简单平均法.

3.投票法

对分类任务最常见的结合策略



应注意：

4.学习法

训练数据很多

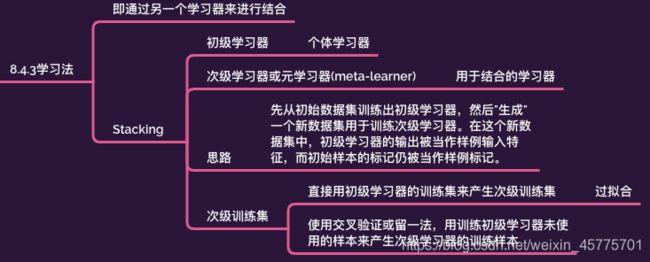
算法描述图如下，这里假定初级学习器使用不同学习算法产生，即初级集成是异质的。

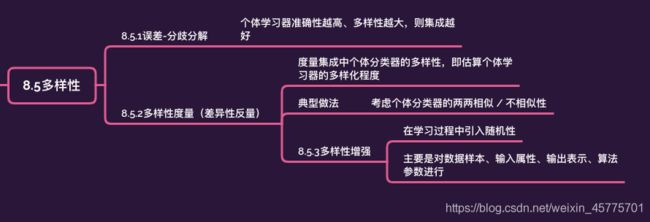
8.5多样性

1.误差-分歧分解

2.多样性度量

用于度量集成中个体分类器的多样性，考虑个体分类器的两两相似性。
两个分类器的预测结果列联表

a,b,c,d为对应预测的样本数目。
常见的多样性度量：

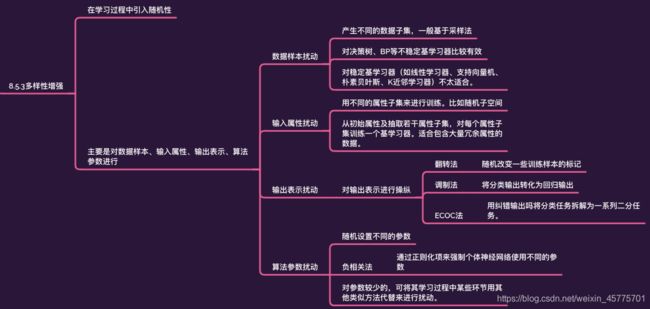
3.多样性增强

输入属性扰动的算法流程

习题

3.自己编程实现一个AdaBoost,以不剪枝决策树为基学习器，在西瓜数据集3.0α上训练一个AdaBoost集成，并与图8.4比较。
链接: link.

4.GradientBoosting是一种常用的Boosting算法，是分析其与AdaBoost的异同。

GradientBoosting与AdaBoost相同的地方在于要生成多个分类器以及每个分类器都有一个权值，最后将所有分类器加权累加起来

不同在于：
AdaBoost通过每个分类器的分类结果改变每个样本的权值用于新的分类器和生成权值，但不改变每个样本不会改变。
GradientBoosting将每个分类器对样本的预测值与真实值的差值传入下一个分类器来生成新的分类器和权值(这个差值就是下降方向)，而每个样本的权值不变。

5.试编程实现Bagging,以决策树桩为学习器，在西瓜数据集3.0α上训练一个Bagging集成，并与8.6进行比较。
链接: link.

以决策树桩作为Bagging的基学习器，效果不太好。尝试了下，设置基学习器数量为21时算是拟合最好的，决策边界如下：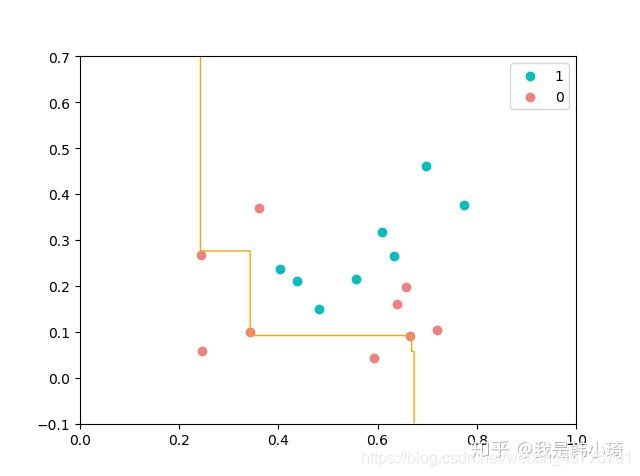

8.6 试析 Bagging 通常为何难以提升朴素贝叶斯分类器的性能.

Bagging主要是降低分类器的方差，而朴素贝叶斯分类器没有方差可以减小。对全训练样本生成的朴素贝叶斯分类器是最优的分类器，不能用随机抽样来提高泛化性能。

7.试述随即森林为什么比决策树Bagging集成的训练速度快。

随机森林不仅会随机样本，还会在所有样本属性中随机几种出来计算。这样每次生成分类器时都是对部分属性计算最优，速度会比Bagging计算全属性要快。

8.MultiBoosting算法与Iterative Bagging的优缺点。

MultiBoosting由于集合了Bagging，Wagging，AdaBoost，可以有效的降低误差和方差，特别是误差。但是训练成本和预测成本都会显著增加。
Iterative Bagging相比Bagging会降低误差，但是方差上升。由于Bagging本身就是一种降低方差的算法，所以Iterative Bagging相当于Bagging与单分类器的折中。

9.试设计一种可视化多样性度量，并与k-误差图比较。

暂无

10.试设计一种能提升k近邻分类器性能的集成学习算法。

可以使用Bagging来提升k近邻分类器的性能，每次随机抽样出一个子样本，并训练一个k近邻分类器，对测试样本进行分类。最终取最多的一种分类。