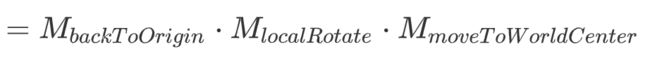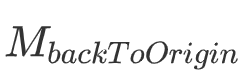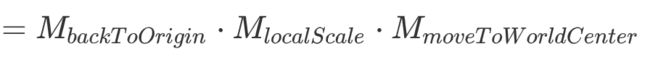GIS数据处理-cesium中模型位置设置
GIS数据处理-cesium中模型位置设置
介绍
最近我收到不少人私信询问我,在cesium中加载3dtiles模型后如何调整模型位置,这里我就统一的介绍一下,我是怎么处理的以供大家参考。
常见模型分类:
- 倾斜摄影模型:由于模型带地理位置,基本上不需要调整模型位置。
- 人工模型:模型是没有坐标信息的,这个时候就需要我们调整模型位置。
还有点云等数据,这里就不介绍了。
我在这里推荐两个方法,一个是使用cesiumlab来操作(可视化操作),另一个是使用代码操作
代码原理
cesium中加载3dtiles模型代码如下:
viewer.scene.primitives.add(new Cesium.Cesium3DTileset({
url: 'http://localhost:8080/data/testModel/tileset.json',
modelMatrix: Cesium.Matrix4.fromArray(
[0.9972458032561666, 0.04372029028528979, 0.05991113506964879, 0,
-0.03623787897545647, 0.9920229449104262, -0.12073646051879428, 0,
-0.06471185374661931, 0.11823287609043515, 0.9908750491338749, 0,
-663.0794944260269, 1211.490494620055, 2974.1003134818748, 1]),
}));
new Cesium.Cesium3DTileset(options)
用于流式传输海量异构 3D 地理空间数据集
options选项
| 名称 | 类型 | 默认 | 描述 |
|---|---|---|---|
| url | 网络资源,字符串 | 瓦片集 JSON 文件的 url | |
| modelMatrix | 矩阵4(Matrix4) | Matrix4.IDENTITY | 转换瓦片集的根瓦片的 4x4 转换矩阵 |
这里我们要详细讲述一下矩阵的用处,cesium中所有的坐标最后都会转换成空间笛卡尔坐标也就是我们常说的三维空间坐标系。在笛卡尔坐标系中模型进行坐标系转换,这里就涉及到转换矩阵了。
tileset.modelMatrix,使用这个属性就可以在数据基础上进行坐标转换了
平移思路
- 获取当前瓦片数据集的包裹范围(boundingSphere)中心(此时参考系是三维笛卡尔坐标系)
- 计算当参考系是局部坐标(局部坐标系的原点为模型包围范围的中心)时,此位置为原点的局部坐标系,到世界坐标的转换矩阵(eastNorthUpToFixedFrame)
- 利用上一步的转换矩阵,左乘一个局部平移向量,得到此平移向量在世界坐标系下的平移目标位置(矩阵×向量,结果是向量)
- 向量相减:世界坐标系下,指向平移目标点位的目标向量 - 指向数据集中心的向量,得到世界坐标系下的平移向量。
- 将世界坐标系下的平移向量转换成平移矩阵,赋予
tileset.modelMatrix
代码实现
tileset
.readyPromise
.then(tileset => {
// Cartesian3 三维笛卡儿坐标系中的瓦片中心点
const tileset_center = tileset.boundingSphere.center;
// Matrix4(四阶矩阵)局部参考系到世界参考系下的转换矩阵
const frompoint_to_world_matrix = Cesium.Transforms.eastNorthUpToFixedFrame(tileset_center);
// 向模型中心为原点,正北为y,正东为x,地心朝上为z分别平移 310、-140、10米
const local_translation = new Cesium.Cartesian3(310, -140, 10);
const result = new Cesium.Cartesian3(0,0,0);
// 转换矩阵左乘局部平移向量,结果存储在 result 中,结果是世界坐标下的平移终点向量
Cesium.Matrix4.multiplyByPoint(frompoint_to_world_matrix, local_translation, result);
const targetpoint_to_world_matrix = Cesium.Transforms.eastNorthUpToFixedFrame(result);
// 世界坐标系下,指向平移目标点位的目标向量 - 指向数据集中心的向量,得到世界坐标系下的平移向量
const world_translation = new Cesium.Cartesian3(
targetpoint_to_world_matrix[12] - frompoint_to_world_matrix[12],
targetpoint_to_world_matrix[13] - frompoint_to_world_matrix[13],
targetpoint_to_world_matrix[14] - frompoint_to_world_matrix[14],
);
// 构造平移矩阵并赋值
tileset.modelMatrix = Cesium.Matrix4.fromTranslation(world_translation);
// 相机视角移动到模型位置
viewer.zoomTo(tileset);
});
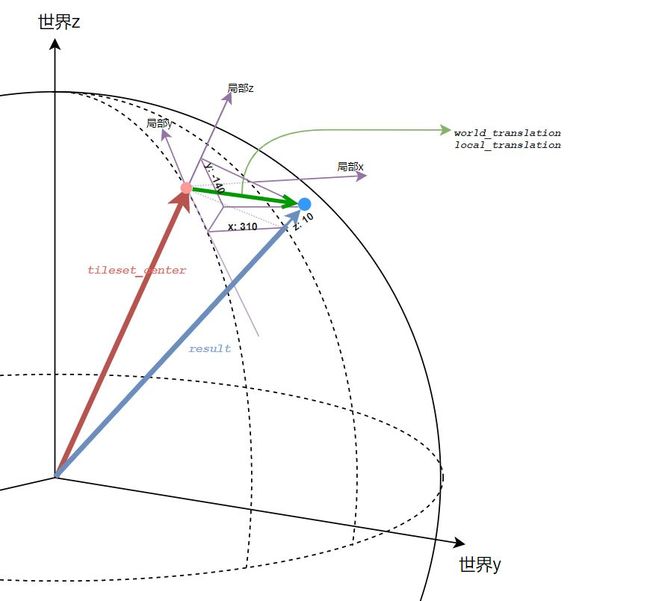
- 红点:frompoint(模型包围范围中心点,也是局部坐标系原点)
- 蓝点:targetpoint(frompoint局部坐标向东向北向上偏移各 310、-140、10米 后得到的目标点)
- 红向量:世界坐标系下的模型包围范围中心点(局部坐标系原点、起始点)向量
- 蓝向量:世界坐标系下的目标点向量
- 绿向量:平移向量。如果是局部坐标,那么就是 (310, -140, 10),如果是世界坐标下的,那就是 蓝向量 - 红向量
cesium 的场景数据最终都是世界坐标的,所以要求的是绿向量的世界坐标表达,然后构造平移矩阵。
现在是已知红向量和局部坐标的绿向量,要先求蓝向量,才能得到世界坐标系下的绿向量。
旋转思路
局部旋转,先将模型移动到世界坐标中心,旋转后,再移动到原来的地方,即
tileset.modelMatrix
其中,
是一个平移矩阵,只需使用模型中心向量取个负值即可
则是从世界坐标中心再移动到模型原点
注意,这里是左乘优先顺序,从右往左乘。
代码实现
tileset
.readyPromise
.then(tileset => {
const tileset_center = tileset.boundingSphere.center; // Cartesian3 三维笛卡儿坐标系中的瓦片中心点
// Matrix4(四阶矩阵)局部参考系到世界参考系下的转换矩阵
const backto_matrix = Cesium.Matrix4.fromTranslation(tileset_center);
// 模型向量取负值
const moveto_vec = Cesium.Cartesian3.multiplyByScalar(tileset_center, -1, new Cesium.Cartesian3());
//移动到世界坐标系原点的矩阵
const moveto_matrix = Cesium.Matrix4.fromTranslation(moveto_vec);
/* 绕x(即东方轴)转90度 */
const cos_rotateX = Math.cos(Math.PI/2);
const sin_rotateX = Math.sin(Math.PI/2);
const arr = [1,0,0,0, 0, cos_rotateX, sin_rotateX,0, 0,-sin_rotateX,cos_rotateX,0, 0,0,0,1];
//旋转矩阵
const rotateX_matrix = Cesium.Matrix4.fromArray(arr);
/* 计算最终矩阵 */
// 获得在世界原点旋转后的矩阵
const temp = Cesium.Matrix4.multiply(rotateX_matrix, moveto_matrix, new Cesium.Matrix4());
// 获得旋转后移动回原来位置的矩阵
const r = Cesium.Matrix4.multiply(backto_matrix, temp, new Cesium.Matrix4());
tileset.modelMatrix = r; // 构造平移矩阵并赋值
// 相机视角移动到模型位置
viewer.zoomTo(tileset);
});
缩放思路
缩放思路和旋转类似,先移动到世界坐标系中心,缩放,然后再移动到原来的地方
tileset.modelMatrix
代码实现
待实现
参考大佬原文
工具使用
上面介绍了代码的实现步骤,现在介绍直接使用工具的方式
cesiumlab
不得不再次推荐,国人良心工具cesiumlab,下载安装即可
步骤
生成3dtiles切片的教程我之前已经写了,这里默认大家都准备好了
我这里使用的是人工建模的模型,没有地理坐标信息,方便给大家演示
加载数据
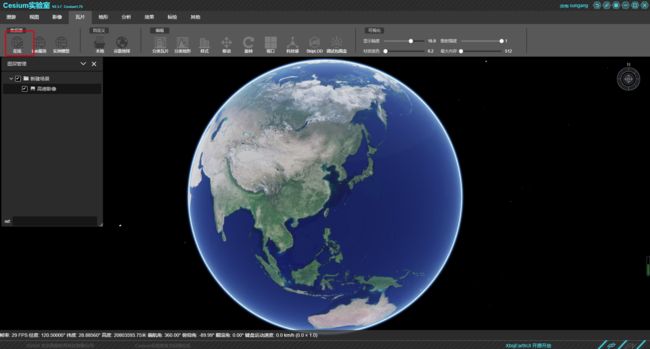
打开cesiumlab,选择三维可视化
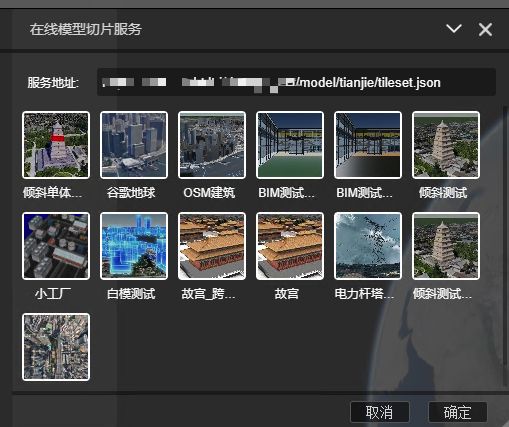
选择瓦片-》在线
填入自己在线的3dtiles地址
右击图层,选择定位,由于人工模型没有坐标信息,cesiumlab会把模型加载到北京天安门
操作数据
右击开启拖拽移动,会在模型包围范围中心出现局部坐标系
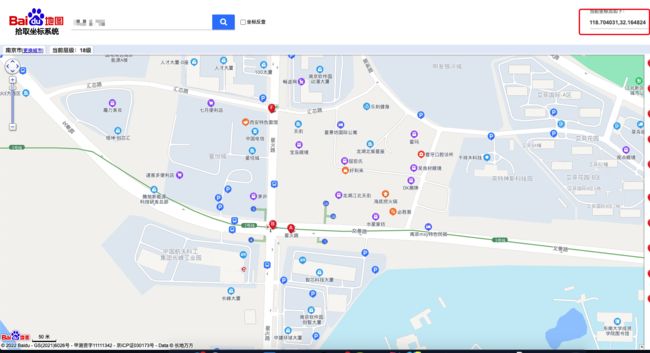
我们先确定一下模型真实的地理位置,这里可以通过百度经纬度查询系统来查询一下模型的真实位置(注意:百度的坐标系是在火星坐标系上二次加密的,因此不会太准,不过没关系我们只是参考)
118.704031,32.164824
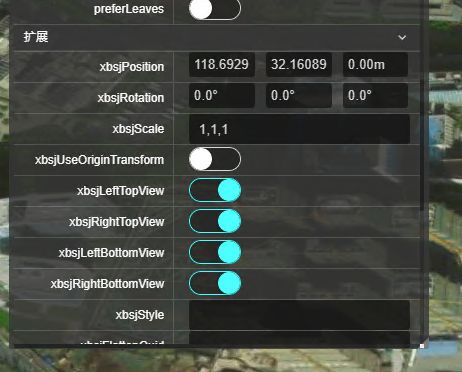
右击打开属性-》看到扩展(xbsjPosition),将坐标赋值进去
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-dnIk9cYZ-1650542433989)(http://qiliu.sunbt.ltd/qiliu_PicGo/image-20220421193827289.png)]
填完后模型会消失,不要担心,它只是去了它该去的地方了
右击定位,我们就能看到它了,如图所示它离真实的地理位置还差一点
这里我们就需要手动调整一下了,我们需要拖拽红、绿、蓝三个方向(红为x轴、绿为y轴、蓝为y轴)
通过拖拽模型已经到了正确的位置了,到这我们已经成功了90%了
获取cesium加载代码
到上面为止,如果模型尺寸和方向没为题,我们就可以获取cesium的加载代码了
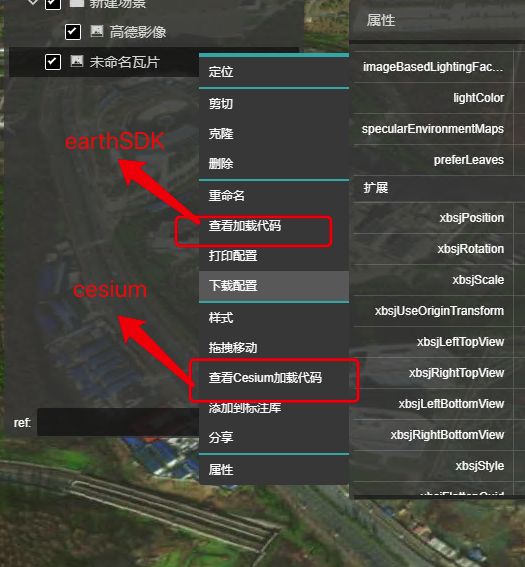
cesiumlab提供了两种加载代码:一种cesium原生的加载代码,一种是earthSDK(也是他们家的,一个基于cesium源码二次开发包,很好用帮我们实现了很多功能,后面有机会也要好好介绍一下)
点击查看cesium加载代码
// cesium加载代码
var viewer = earth.czm.viewer;
var tileset = viewer.scene.primitives.add(new Cesium.Cesium3DTileset({
url: '../model/tianjie/tileset.json',
modelMatrix: Cesium.Matrix4.fromArray([0.9972459143270339,0.043718663325275964,0.05991047350079684,0,-0.03623642613173875,0.9920231602439527,-0.12073512728614089,0,-0.06471095563532905,0.11823167095432924,0.990875251585238,0,-663.0708428965881,1211.4791529159993,2974.063367189374,1]),
}));
viewer.flyTo(tileset);
其中modelMatrix(转换矩阵)已经帮我们计算好了(学习cesium就是这么简单)
我们把它放到自己的代码种就能使用了
参数介绍
扩展种有很多参数,这里介绍一下常用的参数
xbsjPosition:包括经纬度和模型高程
xbsjRotation:这里设置模型在x、y、z轴上旋转的度数
xbsjScale:这里默认是1,表示模型不缩放,修改这三个参数,可以在x、y、z轴上缩放
最好大家都使用一下,就明白怎么做了,太方便了
这些修改好的参数都会计算在转换矩阵中,我们最后只要矩阵参数即可
cesiumlab中还有很多功能,大家可以使用看看