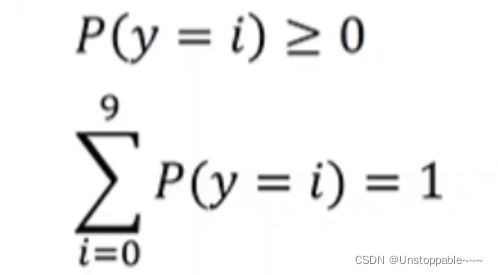pytorch搭建多层神经网络解决多分类问题（采用MNIST数据集）

前置知识可以参考同系列文章：
pytorch完成线性回归任务
pytorch实现逻辑回归

pytorch搭建神经网络解决多分类问题

softmax

核心：最后一层使用softmax层

1.求指数将负值转化为非负值

2.分母将所有输出求和（归一化）

保证条件如下：

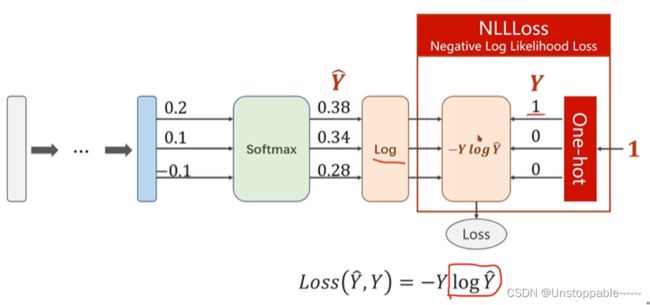
损失函数

使用负对数似然函数（只有y=1的项才真正被计算，为0不影响结果）：

交叉熵损失函数的使用

1.不需要单独使用sofmax（已经被包含在CrossEntropyLoss()函数中）

2.y需要为长整型张量，使用LongTensor()进行构造

import torch

y = torch.LongTensor([0])
z = torch.Tensor([[0.2, 0.1, -0.1]])
criterion = torch.nn.CrossEntropyLoss()
#交叉熵损失也包括了softmax，所以不需要单独似乎用激活函数
loss = criterion(z, y)
print(loss)

多分类的实现

数据的准备

注意：

1.神经网络希望输入的数值较小，最好在0-1之间，所以需要先将原始图像(0-255的灰度值)转化为图像张量（值为0-1）
2.通道：仅有灰度值->单通道 RGB -> 三通道

3.读入的图像张量一般为W * H* C (宽、高、通道数) 在pytorch中要转化为C * W * H

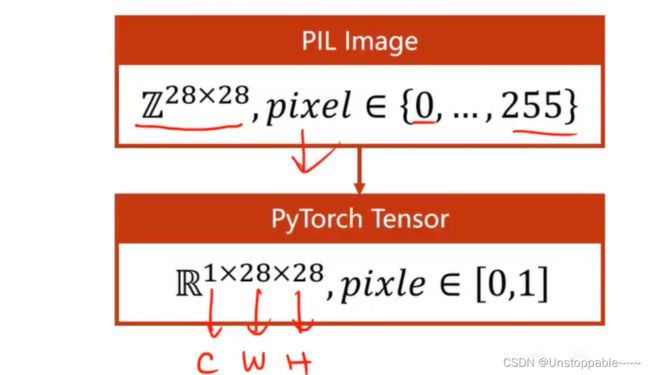
在本例中需要将输入的图像数据（如下图所示）:

a由(28，28)转化为（1， 28， 28）

b数值范围从{0，…，255}转化为{0，…，1}

这一步可以由transfroms中的ToTensor()完成

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import  DataLoader
import torch.nn.functional as F #使用functional中的ReLu激活函数
import torch.optim as optim

#数据的准备
batch_size = 64
#神经网络希望输入的数值较小，最好在0-1之间，所以需要先将原始图像(0-255的灰度值)转化为图像张量（值为0-1）
#仅有灰度值->单通道   RGB -> 三通道 读入的图像张量一般为W*H*C (宽、高、通道数) 在pytorch中要转化为C*W*H
transform = transforms.Compose([
    #将数据转化为图像张量
    transforms.ToTensor(),
    #进行归一化处理，切换到0-1分布 （均值， 标准差）
    transforms.Normalize((0.1307, ), (0.3081, ))
])

train_dataset = datasets.MNIST(root='../dataset/mnist/',
                               train=True,
                               download=True,
                               transform=transform
                               )
train_loader = DataLoader(train_dataset,
                          shuffle=True,
                          batch_size=batch_size
                          )
test_dataset = datasets.MNIST(root='../dataset/mnist/',
                               train=False,
                               download=True,
                               transform=transform
                               )
test_loader = DataLoader(test_dataset,
                          shuffle=False,
                          batch_size=batch_size
                          )

构建模型、损失函数及优化器

注：在ToTensor处理完后，选取batch_size为一组后，数据为（N， 1， 28，28）我们需要将其转化为可以输入的矩阵形式，将（1， 28， 28）变为一维的向量(784, ) 生成的输入矩阵为（N， 784）

#构建模型
class Net(torch.nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.l1 = torch.nn.Linear(784, 512)
        self.l2 = torch.nn.Linear(512, 256)
        self.l3 = torch.nn.Linear(256, 128)
        self.l4 = torch.nn.Linear(128, 64)
        self.l5 = torch.nn.Linear(64, 10)

    def forward(self, x):
        x = x.view(-1, 784) #将数据转化为二维矩阵，可输入神经网络
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        return self.l5(x)    #最后一层不需要激活函数，后面会接入softmax

model = Net()

#设置损失函数和优化器
criterion = torch.nn.CrossEntropyLoss()
#神经网络已经逐渐变大，需要设置冲量momentum=0.5
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)

训练及测试部分

#训练
#将一次迭代封装入函数中
def train(epoch):
    running_loss = 0.0
    for batch_idx, data in enumerate(train_loader, 0):   #在这里data返回输入:inputs、输出target
        inputs, target = data
        optimizer.zero_grad()

        #前向 + 反向 + 更新
        outputs = model(inputs)
        loss = criterion(outputs, target)
        loss.backward()
        optimizer.step()

        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss: %.3f' % (epoch + 1, batch_idx + 1, running_loss / 300))


def test():
    correct = 0
    total = 0
    with torch.no_grad():  #不需要计算梯度
        for data in test_loader:   #遍历数据集中的每一个batch
            images, labels = data  #保存测试的输入和输出
            outputs = model(images)#得到预测输出
            _, predicted = torch.max(outputs.data, dim=1)#dim=1沿着索引为1的维度(行)
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
    print('Accuracy on test set:%d %%' % (100 * correct / total))

if __name__ == '__main__':
    for epoch in range(10):
        train(epoch)
        test()

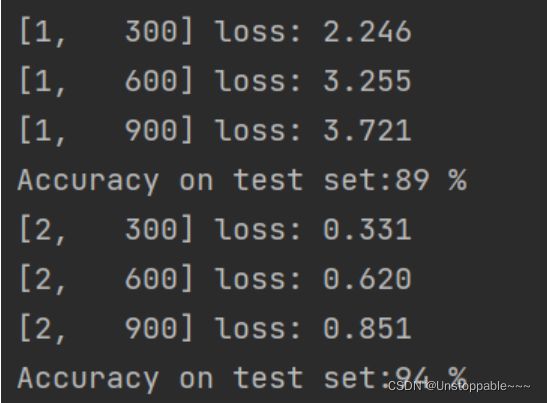
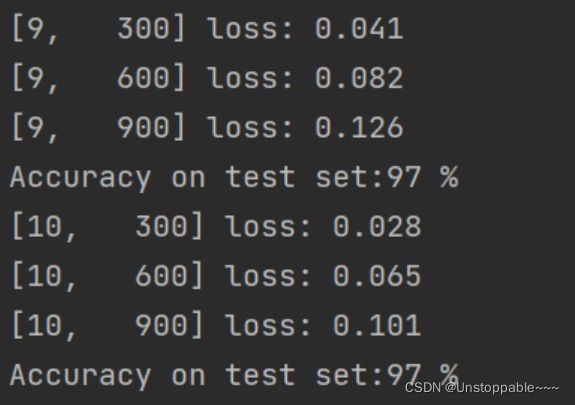
训练结果

如下图所示，从第一个batch开始，没个batch内输出三次损失值，和一次准确率

经过十次迭代后，准确率上升到了97%，损失值也几近收敛