【迎战蓝桥】 算法·每日一题（详解+多解）-- day2

目录

1. 斐波那契数列

2. 青蛙跳台阶问题 

3. 矩形覆盖

---

【大家好，我是爱干饭的猿，如果喜欢这篇文章，点个赞，关注一下吧，后续会一直分享题目与算法思路】

1. 斐波那契数列

 

解题思路：

斐波那契数列是 0 1 1 2 3 5 8 13 21 ...

解题方式很多，有递归方式，也有动归(迭代)方式，但是都是最简单的方式

1. 方法一：递归，return Fibonacci1(n - 1)+Fibonacci1(n - 2);

2. 方法二：迭代方案定义a = 1,b = 1, 第三个数就是 c = a + b,然后一直遍历到c = n结束遍历；

3. 方法三：直接用最简单的方法一，可能因为代码空间复杂度过高，过不了OJ，所以我们可以采用map进行“剪枝”，将每个斐波那契数记录在map中，用时直接在map取用即可。

方法一：代码如下：

    // 递归 但是此算法时间复杂度太大
    public static int Fibonacci1(int n) {
        if(n == 1 || n ==2){
            return 1;
        }
        return Fibonacci1(n - 1)+Fibonacci1(n - 2);
    }

方法二：代码如下：

    // 迭代 a,b,c
    public static int Fibonacci2(int n) {
        if(n == 1 || n ==2){
            return 1;
        }
        int a = 1;
        int b = 1;
        int c =0;
        for (int i = 3; i <= n; i++) {
            c = a + b;
            a = b;
            b = c;
        }
        return c;
    }

方法三：代码如下：

    // “减枝”思想，利用Map 将已得到的fib 存储起来
    private Map  filter = new LinkedHashMap<>();
    public int Fibonacci3(int n) {
        if(n == 0){
            return 0;
        }
        if(n == 1 || n == 2){
            return 1;
        }

        int pre = 0;
        if(filter.containsKey(n-1)){
            // filter 已存在n-1的斐波那契数
            pre = filter.get(n-1);
        }else {
            // 不存在
            pre = Fibonacci3(n - 1);
            // 将该pre 存入filter中
            filter.put(n-1,pre);
        }

        int ppre = 0;
        if( filter.containsKey(n - 2)){
            // filter 已存在n-2的斐波那契数
            ppre = filter.get(n-2);
        }else {
            ppre = Fibonacci3(n-2);
            filter.put(n - 2,ppre);
        }

        return pre + ppre;
    }

2. 青蛙跳台阶问题 

描述：

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法（先后次序不同算不同的结果）。

数据范围：1 ≤ n ≤ 40

要求：时间复杂度：O(n)O(n) ，空间复杂度： O(1)O(1)

解题思路：

方法一：状态定义：f(i): 跳到i台阶的总跳法 

              状态递推：f(i) = f(i-1)+f(i-2)

              初始状态:  f(0) = 1

（0台阶，就是起点，到达0台阶的方法有一种，就是不跳[这里可能有点奇怪，但是想想，如果方 法次数为0，就说明不可能开始...]）, f(1) = 1;

方法二： 当我们写完方法一，在仔细看看这个代码，难道不像上题的斐波那契数列吗？

方法三：因此也可以用递归来写；

方法四：“剪枝”递归；

方法一：代码如下：

    public int jumpFloor0(int target) {
        if(target == 1){
            return 1;
        }
        if(target == 2){
            return 2;
        }
        int[] dp = new int[target + 1];
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 2;

        for (int i = 3; i <= target ; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        int num = dp[target];
        return num;
    }

方法二：代码如下：

    // 迭代
    public int jumpFloor1(int target) {
        if(target == 1){
            return 1;
        }
        if(target == 2){
            return 2;
        }
        int a = 1;
        int b = 2;
        int c = 0;
        for(int i = 3;i <= target; i++){
            c = a + b;
            a = b;
            b = c;
        }
        return c;
    }

方法三：代码如下：

    // 递归
    public int jumpFloor2(int target) {
        if(target == 1){
            return 1;
        }
        if(target == 2){
            return 2;
        }
        return jumpFloor2(target -1) + jumpFloor2(target -2);
    }

方法四：代码如下：

    // 减枝
    private Map filter = new HashMap<>();
    public int jumpFloor(int target) {
        if(target == 1){
            return 1;
        }
        if(target == 2){
            return 2;
        }

        int pre = 0;
        if(filter.containsKey(target - 1)){
            pre = filter.get(target - 1 );
        }else {
            pre = jumpFloor(target - 1);
            filter.put(target - 1,pre);
        }

        int ppre = 0;
        if(filter.containsKey(target - 2)){
            pre = filter.get(target - 2);
        }else {
            ppre = jumpFloor(target - 2);
            filter.put(target - 2,ppre);
        }

        return pre + ppre;
    }

3. 矩形覆盖

描述：

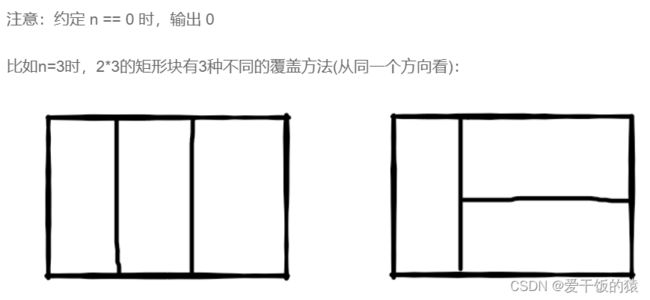
我们可以用 2*1 的小矩形横着或者竖着去覆盖更大的矩形。请问用 n 个 2*1 的小矩形无重叠地覆盖一个 2*n 的大矩形，从同一个方向看总共有多少种不同的方法？

数据范围：0 ≤ n ≤ 38 
进阶：空间复杂度 O(1)\O(1)  ，时间复杂度 O(n)\O(n) 

解题思路：

方法一：我们发现要覆盖 2*1 的矩形，只有1种方法，要覆盖 2*2 的矩形，只有2种方法，（两个2*1的矩形横着放或竖着放）

我们继续使用dp来进行处理，当然后续会发现，斐波那契数列的方式也可以处理，

              状态定义：f(n) : 用n个2*1的小矩形无重叠地覆盖一个2*n的大矩形所用的总方法数

              状态递推：f(n) = f(n-1)【最后一个竖着放】 + f(n-2)【最后两个横着放】 

              初始化：   f(1) = 1,f(2) = 2,f(0)=1,注意f(0)我们这个可以不考虑，如果考虑值设为1，参考上题（这点确实有点蛋疼）

方法二、三、四 和上题(2. 青蛙跳台阶问题)一样，因此不再赘述。

 方法一：代码如下：

    public int rectCover(int target) {
        if(target <= 2){
            return target;
        }

        int[] dp = new int[target + 1];
        dp[0] = 0;
        dp[1] = 1;
        dp[2] = 2;

        for (int i = 3; i <= target ; i++) {
            dp[i] = dp[i - 1] + dp[i - 2];
        }
        int num = dp[target];
        return num;
    }