手撕代码之二叉树
文章目录
- 一、根据排序数组构造二叉搜索树(leetcode 108)
- 二、根据前序遍历和中序遍历构造二叉树(leetcode 105)
- 三、二叉树的非递归遍历(leetcode 94、144、145)
- 四、二叉树中和为某一值的路径(leetcode 112)
- 五、二叉树的最大深度(leetcode 104)
- 六、二叉树的层次遍历(leetcode 102)
- 七、判断两个二叉树是否相同(leetcode 100)
- 八、判断二叉树是否对称(leetcode 101)
- 九、二叉树的右视图(leetcode 199)
- 十、多叉树的遍历
- 十一、二叉树的最小高度(leetcode 111)
- 十二、二叉树的最长路径/宽度/直径(leetcode 543)
- 十三、二叉搜索树第K小的结点(leetcode 230)
- 十四、二叉树的最大路径和(leetcode 124)
- 十五、二叉搜索树的最低公共祖先(leetcode 235)
- 十六、普通二叉树的最低公共祖先(leetcode 236)
- 十七、普通二叉树(带有父指针)的最低公共祖先
- 十八、按之字形打印二叉树(leetcode 103)
- 十九、判断一棵树是否是平衡二叉树(leetcode 110)
二叉树这类题,首先想到递归,然后把大问题分解到最小的问题,即只有根节点和左右子树的情况,先分析这一棵小树,找到递归的出口。
一、根据排序数组构造二叉搜索树(leetcode 108)
思路:以数组的中点划分左右子树。
class Solution {
public:
TreeNode* sortedArrayToBST(vector<int>& nums) {
if (nums.size() == 0)
return nullptr;
return sortedArrayToBSTCore(nums, 0, nums.size()-1);
}
TreeNode* sortedArrayToBSTCore(vector<int>& nums, int low, int high){
if (low > high) return nullptr;
int mid = low + (high - low) / 2;
TreeNode *node = new TreeNode(nums[mid]);
node->left = sortedArrayToBSTCore(nums, low, mid-1);
node->right = sortedArrayToBSTCore(nums, mid+1, high);
return node;
}
};
二、根据前序遍历和中序遍历构造二叉树(leetcode 105)
思路:哈希表记录下中序遍历元素及对应的位置,根据前序遍历找根结点,通过哈希表找到根结点在中序遍历中的位置,根据该位置划分左右子树。
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
unordered_map<int, int> mp;
for (int i = 0; i < inorder.size(); ++i){
mp[inorder[i]] = i;
}
return buildTreeCore(preorder, 0, preorder.size() - 1, inorder, 0, inorder.size() - 1, mp);
}
TreeNode* buildTreeCore(vector<int>& preorder, int pBegin, int pEnd,
vector<int>& inorder, int iBegin, int iEnd,
unordered_map<int, int> &mp){
if (pBegin > pEnd) return nullptr;
TreeNode *root = new TreeNode(preorder[pBegin]);
int mid = mp[preorder[pBegin]];
root->left = buildTreeCore(preorder, pBegin+1, pBegin+mid-iBegin, inorder, iBegin, mid-1, mp);
root->right = buildTreeCore(preorder, pBegin+mid-iBegin+1, pEnd, inorder, mid+1, iEnd, mp);
return root;
}
};
三、二叉树的非递归遍历(leetcode 94、144、145)
class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int> vec;
if (root == nullptr) return vec;
// 先将根节点入栈
stack<TreeNode*> st;
st.push(root);
while (!st.empty()){
// 取栈顶元素并弹出
TreeNode *node = st.top(); st.pop();
vec.push_back(node->val);
// 再将右子树和左子树入栈
if (node->right != nullptr) st.push(node->right);
if (node->left != nullptr) st.push(node->left);
}
return vec;
}
};
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
vector<int> vec;
stack<TreeNode*> st;
TreeNode *node = root;
while (node || !st.empty()){
// 先将左子树的结点全部入栈
if (node){
st.push(node);
node = node->left;
}
else{
// 取栈顶元素并访问其右子树
vec.push_back(st.top()->val);
node = st.top()->right;
st.pop();
}
}
return vec;
}
};
四、二叉树中和为某一值的路径(leetcode 112)
思路:访问了当前结点后,剩下的问题变成了在当前结点的左右子树寻找和为sum-root->val的问题,所以明显是递归。
class Solution {
public:
bool hasPathSum(TreeNode* root, int sum) {
if (root == nullptr) return false;
if (root->left == nullptr &&
root->right == nullptr &&
root->val == sum) return true;
return hasPathSum(root->left, sum-root->val) ||
hasPathSum(root->right, sum-root->val);
}
};
五、二叉树的最大深度(leetcode 104)
思路:二叉树的最大深度等于左右子树的最大深度中的较大者+1。
class Solution {
public:
int maxDepth(TreeNode* root) {
if (root == nullptr) return 0;
return max(maxDepth(root->left), maxDepth(root->right)) + 1;
}
};
六、二叉树的层次遍历(leetcode 102)
思路:广搜用队列保存每一行的结果,队列的长度表示二叉树每一层有多少个节点。
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> res;
if (root == nullptr) return res;
queue<TreeNode*> que;
que.push(root);
vector<int> vec_tmp;
while (!que.empty()){
int len = que.size();
for (int i = 0; i < len; ++i){
TreeNode *node = que.front();
que.pop();
vec_tmp.push_back(node->val);
if (node->left != nullptr)
que.push(node->left);
if (node->right != nullptr)
que.push(node->right);
}
res.push_back(vec_tmp);
vec_tmp.clear();
}
return res;
}
};
七、判断两个二叉树是否相同(leetcode 100)
思路:两棵树相同当且仅当两个结点相同、左右子树也相同
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
if (p == nullptr && q == nullptr) return true;
if (p == nullptr || q == nullptr) return false;
return p->val == q->val &&
isSameTree(p->left, q->left) &&
isSameTree(p->right, q->right);
}
};
八、判断二叉树是否对称(leetcode 101)
思路:判断一棵树是否对称相当于判断其左右子树是否对称,左右子树如果是对称的,那么两棵树的当前结点必定相同,并且左右儿子结点对称。
class Solution {
public:
bool isSymmetric(TreeNode* root) {
return root == nullptr || isSymmetricCore(root->left, root->right);
}
bool isSymmetricCore(TreeNode *p, TreeNode *q){
if (p == nullptr && q == nullptr) return true;
if (p == nullptr || q == nullptr) return false;
return p->val == q->val &&
isSymmetricCore(p->left, q->right) &&
isSymmetricCore(p->right, q->left);
}
};
九、二叉树的右视图(leetcode 199)
右视图的意思是从右边看向二叉树能够看到的所有节点,即二叉树每一层最右边的节点。思路:通过层次遍历找到每一层的最右边节点,利用队列。
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
vector<int> res;
if (root == nullptr)
return res;
queue<TreeNode*> que;
que.push(root);
while (!que.empty()){
// 最右边节点
res.push_back(que.back()->val);
int sz = que.size();
for (int i = 0; i < sz; ++i){
TreeNode* tmp = que.front();
que.pop();
if (tmp->left) que.push(tmp->left);
if (tmp->right) que.push(tmp->right);
}
}
return res;
}
};
十、多叉树的遍历
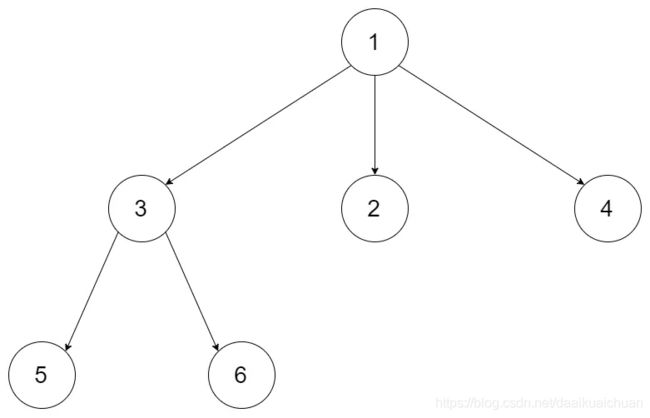
思路:和二叉树的遍历类似,不同的是多叉树每一个节点都有一个儿子节点数组。
void travel(TreeNode* pNode) {
if (pNode == nullptr)
return;
cout << pNode->val << endl;
for (int i = 0 ; i < pNode->child_list.size(); ++i) {
Node *tmp = pNode->child_list[i];
travel(tmp);
}
}
十一、二叉树的最小高度(leetcode 111)

思路:对于当前结点,如果为空,最小高度为0;如果当前节点的左子树为空,最小高就是右子树的最小高度+1;如果当前节点的右子树为空,最小高就是左子树的最小高度+1;如果左右子树都存在,最小高就是左子树的最小高度和右子树的最小高度之间的较小者+1。
class Solution {
public:
int minDepth(TreeNode* root) {
// 对于当前结点,如果为空,最小高度为0
if (root == nullptr)
return 0;
// 如果当前节点的左子树为空,最小高就是右子树的最小高度+1
if (root->left == nullptr)
return 1 + minDepth(root->right);
// 如果当前节点的右子树为空,最小高就是左子树的最小高度+1
if (root->right == nullptr)
return 1 + minDepth(root->left);
// 如果左右子树都存在,最小高就是左子树的最小高度和右子树的最小高度之间的较小者+1
return 1 + min(minDepth(root->left), minDepth(root->right));
}
};
十二、二叉树的最长路径/宽度/直径(leetcode 543)

思路:如果最长路径包含当前节点,则最长路径为其左右子树最大深度之和;如果不包含当前节点,则然后比较和左右子树的最长路径的大小。
class Solution {
public:
int diameterOfBinaryTree(TreeNode* root) {
if (root == nullptr) return 0;
// 如果最长路径包含当前节点,则最长路径为其左右子树最大深度之和
int _maxdepth = MaxDepth(root->left) + MaxDepth(root->right);
// 如果不包含当前节点,则然后比较和左右子树的最长路径的大小
_maxdepth = max(_maxdepth, diameterOfBinaryTree(root->left));
_maxdepth = max(_maxdepth, diameterOfBinaryTree(root->right));
return _maxdepth;
}
// 求二叉树的最大深度
int MaxDepth(TreeNode* root) {
if (root == nullptr) return 0;
return 1 + max(MaxDepth(root->left), MaxDepth(root->right));
}
};
十三、二叉搜索树第K小的结点(leetcode 230)
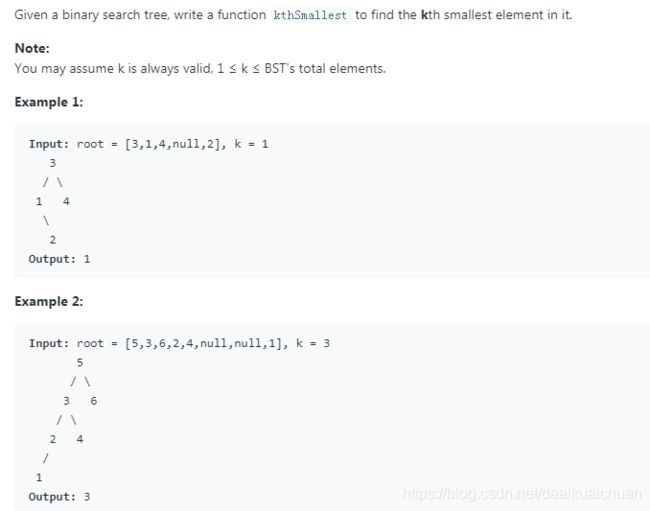
思路:二叉搜索树的中序遍历就是有序数组,可以通过中序遍历找到第K小的节点。
class Solution {
public:
int cnt = 0, res = 0;
int kthSmallest(TreeNode* root, int k) {
preorder(root, k);
return res;
}
// 二叉搜索树的中序遍历就是有序数组,可以通过中序遍历找到第K个最小的节点
void preorder(TreeNode* root, int k) {
if (root != nullptr) {
preorder(root->left, k);
cnt++;
if (cnt == k) {
res = root->val;
return;
}
preorder(root->right, k);
}
}
};
十四、二叉树的最大路径和(leetcode 124)

思路:给定一个非空节点,最终路径经过这个节点有4种情况:1、只有该节点本身(左右子树的路径都是负数);2、该节点+左子树路径;3、该节点+右子树路径;4、该节点+左子树路径+右子树路径。其中1,2,3都可以作为子树路径和向上延伸,而4则不行。
class Solution {
public:
int res = INT_MIN;
int maxPathSum(TreeNode* root) {
maxPathSumCore(root);
return res;
}
int maxPathSumCore(TreeNode* root) {
if (root == nullptr) return 0;
// 过当前节点左子树的最大路径和
int leftsum = maxPathSumCore(root->left);
// 过当前节点右子树的最大路径和
int rightsum = maxPathSumCore(root->right);
// 过当前节点的最大路径和
int cursum = max(root->val, max(leftsum+root->val, rightsum+root->val));
//如果将当前节点作为根节点,就要考虑横跨的情况
res = max(res, max(cursum, root->val + leftsum + rightsum));
return cursum;
}
};
十五、二叉搜索树的最低公共祖先(leetcode 235)

思路:利用二叉搜索树的性质,可以很方便的求解。递归的去求两个节点的最近公共祖先,首先看两个节点的值与当前节点的大小关系,如果两个节点的值一个小于等于当前节点值,另一个大于等于当前节点的值,那么这个当前节点一定是他们的最近公共祖先;如果两个节点值都要比当前节点值小,那么最近公共祖先应该在左子树里面,递归求解;类似的,如果都大与当前节点的值,那么最近公共祖先应该在右子树里面,递归求解。
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
// 如果两个节点的值一个小于等于当前节点值,另一个大于等于当前节点的值,那么这个当前节点一定是他们的最近公共祖先
if (root->val == p->val || root->val == q->val)
return root;
// 如果两个节点值都要比当前节点值小,那么最近公共祖先应该在左子树里面
if (root->val < p->val && root->val < q->val)
return lowestCommonAncestor(root->right, p, q);
// 如果都大与当前节点的值,那么最近公共祖先应该在右子树里面
if (root->val > p->val && root->val > q->val)
return lowestCommonAncestor(root->left, p, q);
else
return root;
}
};
十六、普通二叉树的最低公共祖先(leetcode 236)

思路:从根节点开始遍历,如果节点1和节点2中的任一个和root匹配,那么root就是最低公共祖先。 如果都不匹配,则分别递归查询左、右子树,如果有一个 节点出现在左子树,并且另一个节点出现在右子树,则root就是最低公共祖先;如果两个节点都出现在左子树,则说明最低公共祖先在左子树中,否则在右子树。
class Solution {
public:
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == nullptr || root->val == p->val || root->val == q->val)
return root;
// 如果两个节点的最近公共祖先在当前节点的左子树上,则递归查询左子树
TreeNode* left = lowestCommonAncestor(root->left, p, q);
// 如果两个节点的最近公共祖先在当前节点的右子树上,则递归查询右子树
TreeNode* right = lowestCommonAncestor(root->right, p, q);
if (left == nullptr)
return right;
if (right == nullptr)
return left;
// 否则当前节点就是最近公共祖先
return root;
}
};
十七、普通二叉树(带有父指针)的最低公共祖先
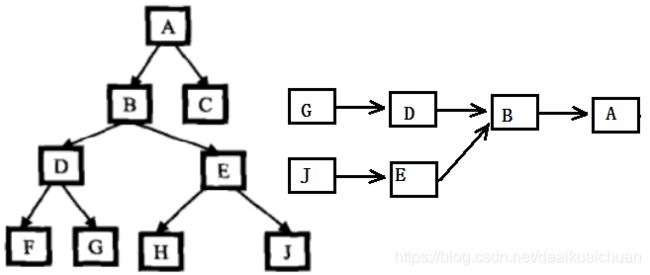
思路:首先给出node1的父节点node1->_parent,然后将node1的所有父节点依次和node2->parent作比较,如果发现两个节点相等,则该节点就是最近公共祖先,直接将其返回,时间复杂度为O(n^2)。如果没找到相等节点,则将node2的所有父节点依次和node1->_parent->_parent作比较…直到node1->_parent==NULL。
TreeNode* GetLastCommonAncestor(TreeNode * root, TreeNode* node1, TreeNode* node2)
{
TreeNode * temp;
while (node1 != NULL){
node1 = node1->_parent;
temp = node2;
while (temp != NULL){
if (node1 == temp->_parent)
return node1;
temp = temp->_parent;
}
}
}
十八、按之字形打印二叉树(leetcode 103)

思路:使用广搜进行层次遍历,并记录层数,如果是偶数则翻转该层的遍历结果。
class Solution {
public:
vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
vector<vector<int>> res;
if (root == nullptr) return res;
// 广搜用队列保存每一行的结果
queue<TreeNode*> que;
que.push(root);
vector<int> vec_tmp;
int i = 0;
while (!que.empty()){
i++;
int len = que.size();
// 队列的长度表示每一层有多少个元素
for (int i = 0; i < len; ++i){
TreeNode *node = que.front();
que.pop();
vec_tmp.push_back(node->val);
if (node->left != nullptr)
que.push(node->left);
if (node->right != nullptr)
que.push(node->right);
}
// 记录层数,偶数层则反转下该层的结果
if (!(i & 1))
reverse(vec_tmp.begin(), vec_tmp.end());
res.push_back(vec_tmp);
vec_tmp.clear();
}
return res;
}
};
十九、判断一棵树是否是平衡二叉树(leetcode 110)

思路:对于每一个节点,我们通过checkDepth方法递归获得左右子树的深度,然后自底而上判断每一个节点是否平衡,如果某一个节点不平衡,则直接返回-1,避免重复判断;如果是平衡的,则直接返回深度,此方法时间复杂度O(N)。
class Solution {
public:
// 自底而上判断每一个节点是否平衡,如果某一个节点不平衡,则直接返回-1,避免重复判断;如果是平衡的,则直接返回深度。
int chechDepth(TreeNode *root) {
if (root == nullptr)
return 0;
int left = chechDepth(root->left);
if (left == -1)
return -1;
int right = chechDepth(root->right);
if (right == -1)
return -1;
// 不满足平衡条件
if (abs(left - right) > 1)
return -1;
else
return 1 + max(left, right);
}
bool isBalanced(TreeNode* root) {
if (chechDepth(root) == -1)
return false;
else
return true;
}
};