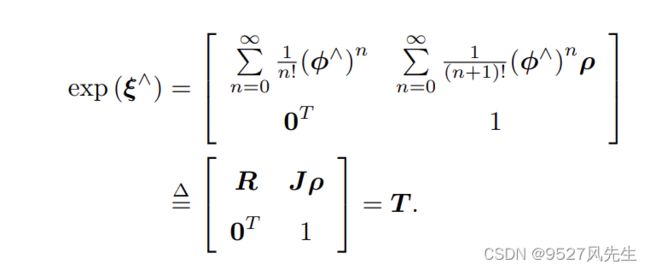视觉SLAM十四讲笔记三（第四讲）

1、引言

在第三讲中介绍了旋转矩阵R、旋转向量、欧拉角、四元数若干种方式，这些仅是对旋转的表示，除了表示我们还需进行估计和优化，因为在SLAM中位姿是未知的，我们需要解决：什么样的相机位姿最符合当前的观测数据，这类问题可以转化为优化问题，即求解最优的R、t 使误差最小化。

但是因为旋转矩阵是有约束的，所以优化变为有有约束优化，这是不好的，由此便引入李代数将其变为无约束优化。

2、李代数与李代数基础

特殊正交群： 

特殊欧式群：

上节介绍了旋转矩阵构成了特殊正交群，变换矩阵构成了特殊欧氏群，如果大家不熟悉，可以回顾我写的==>第三讲<==

旋转矩阵和变换矩阵的缺点：对加法是不封闭的（任意两个旋转矩阵相加不再是一个旋转矩阵）

群的概念：只有一个良好运算的集合（旋转矩阵对加法不封闭，但对乘法封闭（良好运算），=>只有一个良好运算）实在不懂的可以学习下矩阵论。

李群：具有连续（光滑）性质的群。

而刚体能够在空间中连续的进行运动，因此,都是李群。由此便引入了李群的概念。

3、李代数的引出

式4.10里面的ϕ 正是对应到 SO(3) 上的 李代数 so(3)

 每一个李群都有与之对应的李代数，且李代数描述了李群的局部性质。

李括号：群中较为简单的二元运算

李代数SO(3)

上文已经推导出李代数SO(3)，下面给出具体的定义

下面我们说，之前提到的 ϕ，事实上是一种李代数。SO(3) 对应的李代数是定义在 R3 上的向量，我们记作 ϕ。根据前面的推导，每个 ϕ 都可以生成一个反对称矩阵：

李代数SE(3)

 4、指数与对数映射

在此我直接给出SO(3)与SE(3)的指数映射，具体推导过程不再给出。（知道这个概念就好）

 SO(3)的指数映射：

SE(3)的指数映射：

我们看到，平移部分经过指数映射之后， 发生了一次以 J 为系数矩阵的线性变换。请读者重视这里的 J，因为我们后面还要用到它。

最后总结下李群与李代数的关系图

5、 李代数求导与扰动模型

使用李代数是为了优化，有了李代数就可以进行无约束优化，而李代数无法进行乘法，因此引入BHC近似（一个新概念）。

两个李代数指数映射乘积的完整形式，由 Baker-Campbell-Hausdorff 公式（BCH 公 式）①给出。由于它完整的形式较复杂，我们给出它展开式的前几项：

李代数求导

第一种求导后仍然具有较复杂的参数，由此只介绍第二种求导方式

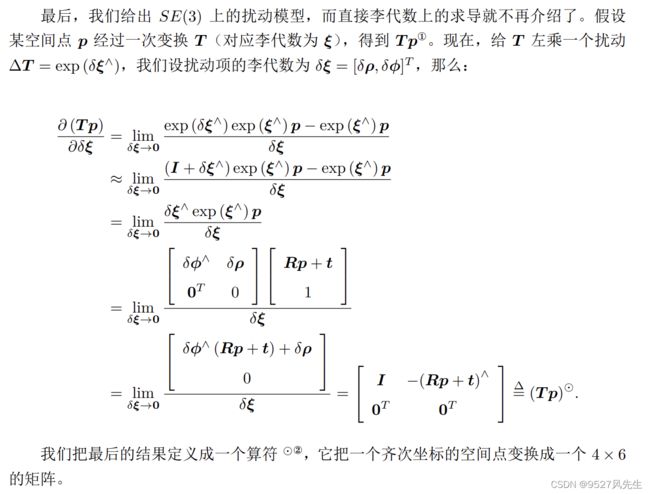
扰动模型求导

6、SE(3)李代数求导 

 7、矩阵求导顺序

 

 8、Sophus模板安装：

1、下载fmt===>fmt

2、编译fmt

cd fmt-8.1.1
mkdir build
cd build
cmake ..
make
sudo make install

 3、Sophus模板安装

git clone https://github.com/strasdat/Sophus.git
cd Sophus
mkdir build
cd build
cmake ..
make
sudo make install