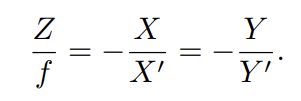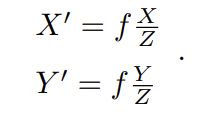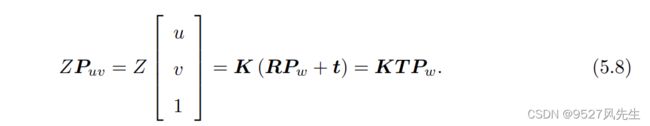视觉SLAM十四讲笔记四(第五讲)
1、相机模型
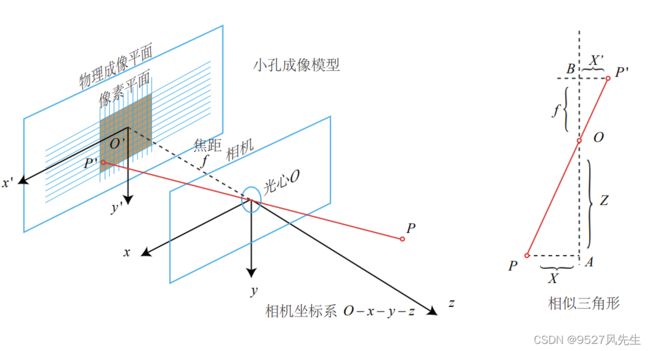
针孔模型:将三维坐标点映射到二维图像平面的几何模型
现在来对这个简单的针孔模型进行几何建模。设 O − x − y − z 为相机坐标系,我们让 z 轴指向相机前方,x 向右,y 向下。O 为摄像机的光心,也是针孔模型中的针孔。现实世界的空间点 P,经过小孔 O 投影之后,落在物理成像平面 O′ − x ′ − y ′ 上,成像点为 P ′。设 P 的坐标为 [X, Y, Z] T,P ′ 为 [X′ , Y ′ , Z′ ] T,并且设物理成像平面到小孔的 距离为 f(焦距)。那么,根据三角形相似关系,有:
其中负号表示成的像是倒立的。为了简化模型,我们把可以成像平面对称到相机前方,和 三维空间点一起放在摄像机坐标系的同一侧:
上式描述了点 P 和它的像之间的空间关系。不过,在相机中,我们最终获得的是 一个个的像素,所以还需将相转换为像素,我们设在物理成像平面上固定着一个像素平面 o − u − v。我们 在像素平面得到了 P ′ 的像素坐标:[u, v] T。
像素坐标系:原点 o ′ 位于图像的左上角,u 轴向右与 x 轴平行,v 轴向下与 y 轴平行。像素坐标系与成像平面之间,相差了一个缩放和一个原点的平移。我 们设像素坐标在 u 轴上缩放了 α 倍,在 v 上缩放了 β 倍。同时,原点平移了 [cx, cy] T。那 么,P ′ 的坐标与像素坐标 [u, v] T 的关系为:
K: 相机内参数矩阵(内参一般在出厂之后是固定的,,若不知道内参,则需要对其进行标定=>张正友标定法)
除了内参之外,自然还有相对的外参。考虑到在式(5.6)中,我们使用的是 P 在相机 坐标系下的坐标。由于相机在运动,所以 P 的相机坐标应该是它的世界坐标(记为 Pw), 根据相机的当前位姿,变换到相机坐标系下的结果。相机的位姿由它的旋转矩阵 R 和平移向量 t 来描述。那么有:
(世界坐标系*R+t)=相机坐标系,相机坐标系左乘相机内参=像素坐标
外参数: 相机的位姿,R,t(外参会随着相机运动发生改变,同时也是 SLAM 中待估计的目标,代表着机器人的轨迹)
由上式看出像素坐标的Z轴背归一化了,说明点的深度在投影中被丢失了,所以单目无法得到像素的深度值。
2、畸变模型
为了获得更好的成像效果,往往在相机的前面加上透镜。
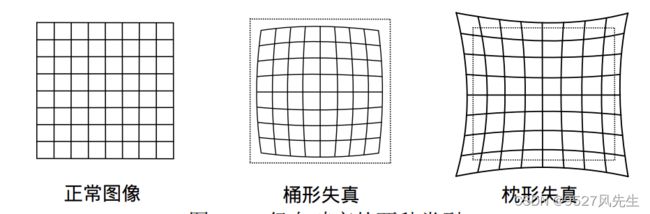
径向畸变:由透镜形状引起的畸变。(桶形畸变,枕形畸变)如下图:
切向畸变:相机的组装过程中,不能使透镜和成像平面严格平行
畸变只需了解即可,在下面给出畸变矫正的公式,相详细了解的读者可自行百度
3、双目相机:
简单介绍,相深入了解可自行百度
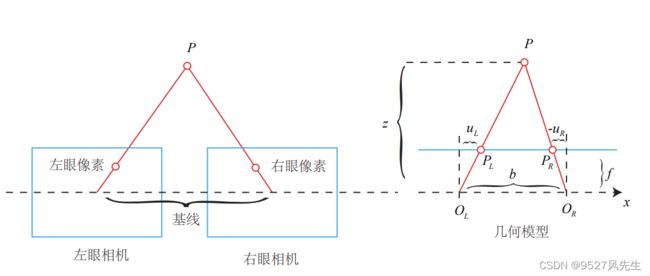
双目相机计算深度原理:通过同步采集左右相机的图像,计算图像间视差,来估计每一个像素的深度。
双目相机一般由左眼和右眼两个水平放置的相机组成。在左右双目的相机中,我们可以把两个相机都看作针孔相机。它们是水平放置的,意味两个相机的光圈中心都位于 x 轴上。它们的距离称 为双目相机的基线(Baseline, 记作 b),是双目的重要参数。
视差:左右图的横坐标之差。根据视差,我们可以估计一 个像素离相机的距离。视差与距离成反比:视差越大,距离越近。
基线:当基线越长 时,双目最大能测到的距离就会变远;反之,小型双目器件则只能测量很近的距离。
4、RGB-D相机模型
相较于双目计算深度的方式,RGB-D更主动,他能够主动测量每个像素的深度。
目前的 RGB-D 相机按原理可分为两大类:
1、通过红外结构光(Structured Light)来测量像素距离(相机需要向探测目标发射一束光线,相机根据返回的结构光图案,计算物体离自身的距离)
2、通过飞行时间法(Time-of-flight, ToF)原理测量像素距离(相机向目标发射脉冲光,然后根据发送到返回之间的光束飞行时间,确定物体离自身的距离。ToF 相机则可以获得整个图像的像素深度)
在测量深度之后,RGB-D 相机通常按照生产时的各个相机摆放位置,自己完成深度 与彩色图像素之间的配对,输出一一对应的彩色图和深度图。我们可以在同一个图像位置, 读取到色彩信息和距离信息,计算像素的 3D 相机坐标,生成点云(Point Cloud)。
缺点:受光干扰,成本,功耗