深度神经网络DNN的反向传播原理及推导
目录
- DNN反向传播推导
-
-
- 1.统一符号
- 2.前向传播
- 3.损失函数
- 4.关于BP的重要说明
- 5.BP推导
- 6.总结一下
-
DNN反向传播推导
1.统一符号
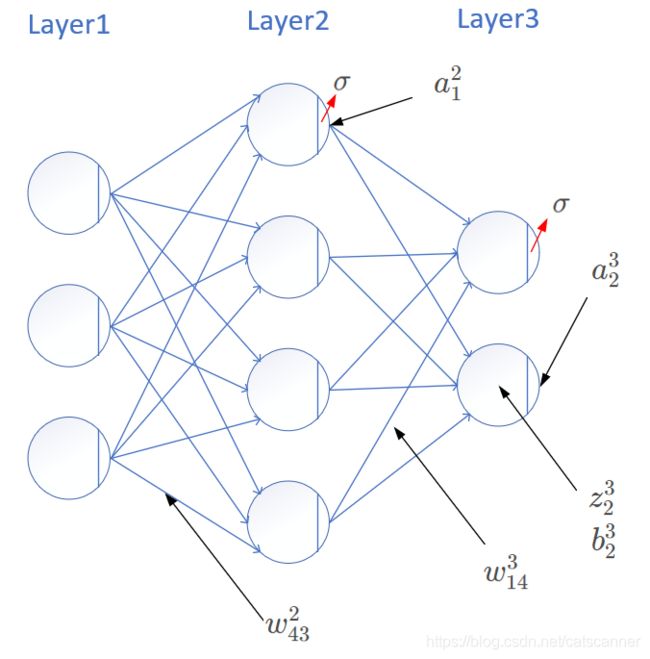
如上图所示,我们先统一一下符号:
w w w 权重
z z z 输入值
b b b 偏置bais
a a a 激活值
σ \sigma σ 激活函数
w 43 2 w_{43}^{2} w432 表示第2层隐层上的第4个神经元上由前一层的第3个神经元链接过来的权重
b 2 3 b_{2}^{3} b23 表示第3层隐层的第二个神经元的偏置
a 1 2 a_{1}^{2} a12 表示第2层隐层上第1个神经元的激活值
z 1 2 z_{1}^{2} z12 表示第2层隐层上第1个神经元的输入值
于是有
z 2 3 = ( a 1 2 w 21 3 + a 2 2 w 22 3 + a 3 2 w 23 3 + a 4 2 w 24 3 ) + b 2 3 z_2^3= (a_1^2w_{21}^3 + a_2^2w_{22}^3 + a_3^2w_{23}^3 +a_4^2w_{24}^3) +b_2^3 z23=(a12w213+a22w223+a32w233+a42w243)+b23
a 2 3 = σ ( z 2 3 ) a_2^3=\sigma(z_2^3) a23=σ(z23)
2.前向传播
好,我们然后用符号代替掉数字:
w j k l w_{jk}^{l} wjkl 表示第l层隐层上的第j个神经元上由前一层的第k个神经元链接过来的权重
b j l b_{j}^{l} bjl 表示第l层隐层的第j个神经元的偏置
a j l a_{j}^{l} ajl 表示第l层隐层上第j个神经元的激活值
z j l z_{j}^{l} zjl 表示第l层隐层上第j个神经元的输入值
于是我们有:
z j l = ∑ k w j k l a k l − 1 + b j l z_j^l=\sum_kw_{jk}^la_k^{l-1}+b_j^l zjl=k∑wjklakl−1+bjl
a j l = σ ( z j l ) = σ ( ∑ k w j k l a k l − 1 + b j l ) a_j^l=\sigma(z_j^l)=\sigma(\sum_kw_{jk}^la_k^{l-1}+b_j^l) ajl=σ(zjl)=σ(k∑wjklakl−1+bjl)
使用向量表示:
a l = σ ( z l ) = σ ( w l a l − 1 + b l ) a^l=\sigma(z^l)=\sigma(w^la^{l-1}+b^l) al=σ(zl)=σ(wlal−1+bl)
3.损失函数
假设我们使用均方误差MSE作为损失函数
C = 1 2 n ∑ x ∥ y ( x ) − a L ( x ) ∥ 2 C=\frac{1}{2n} \sum_x \| y(x)-a^L(x)\|^2 C=2n1x∑∥y(x)−aL(x)∥2
a L a^L aL就是最后一层的激活输出,L代表最后一层, y ( x ) y(x) y(x)代表输入为x时候的Ground Truth
我们写成向量表示:
C = 1 2 ∥ y − a L ∥ 2 = 1 2 ∑ j ( y j − a j L ) 2 C=\frac{1}{2}\|y-a^L\|^2=\frac{1}{2} \sum_j (y_j-a_j^L)^2 C=21∥y−aL∥2=21j∑(yj−ajL)2
我们的目标就是要优化 C C C,使其最小。
4.关于BP的重要说明
对 C C C来说,变量不是输入的 x x x和中间隐层的 a a a,而是 w w w。我们要使用 C 对 w C对w C对w的梯度来做梯度下降,去改变 w w w,以达到一个目的,就是求得一组 w w w使得对输入的所有图像或数据 x x x使 平 均 C 平均C 平均C最小。所以实际上我们在这个问题中最关心的就是 C 对 w C对w C对w的梯度:
∂ C ∂ w j k l \frac{\partial C}{\partial w_{jk}^l} ∂wjkl∂C
以及 C 对 b i a s 的 梯 度 : C对bias的梯度: C对bias的梯度:
∂ C ∂ b j l \frac{\partial C}{\partial b_j^l} ∂bjl∂C
BP反向传播是相对于正向求导计算而言的,那为什么要使用BP反向传播来计算这两个梯度呢?
答案是是因为计算比较快。为什么计算比较快,我们先来看看直接算梯度为什么比较慢.
我们来看这样一个有2个隐层的神经网络,我们要求 ∂ C ∂ w 11 2 \frac{\partial C}{\partial w_{11}^{2}} ∂w112∂C
∂ C ∂ w 11 2 = ∂ ( l o s s ( a 1 4 ) + l o s s ( a 2 4 ) ) ∂ w 11 2 = ∂ ( l o s s ( a 1 4 ) ) ∂ w 11 2 + ∂ ( l o s s ( a 2 4 ) ) ∂ w 11 2 = ∂ C ∂ a 1 4 ∂ a 1 4 ∂ w 11 2 + ∂ C ∂ a 2 4 ∂ a 2 4 ∂ w 11 2 \textcolor{red} { \frac{\partial C}{\partial w_{11}^{2}}=\frac{\partial(loss(a_1^4)+loss(a_2^4))}{\partial w_{11}^{2}} \\ =\frac{\partial(loss(a_1^4))}{\partial w_{11}^{2}} +\frac{\partial(loss(a_2^4))}{\partial w_{11}^{2}} \\ = \frac{\partial C}{\partial a_1^4} \frac{\partial a_1^4}{\partial w_{11}^{2}} + \frac{\partial C}{\partial a_2^4} \frac{\partial a_2^4}{\partial w_{11}^{2}} } ∂w112∂C=∂w112∂(loss(a14)+loss(a24))=∂w112∂(loss(a14))+∂w112∂(loss(a24))=∂a14∂C∂w112∂a14+∂a24∂C∂w112∂a24
假设我们要计算 a 1 4 到 C a_{1}^{4}到C a14到C这条路径,如红色箭头所示, w 11 2 w_{11}^{2} w112影响的所有神经元都要纳入计算
∂ C ∂ a 1 4 容 易 求 得 \textcolor{red}{\frac{\partial C}{\partial a_1^4} 容易求得 } ∂a14∂C容易求得
重 点 看 ∂ a 1 4 ∂ w 11 2 \textcolor{red}{重点看 \frac{\partial a_1^4}{\partial w_{11}^{2}} \\ } 重点看∂w112∂a14
由于 a 1 4 = σ ( z 1 4 ) 而 z 1 4 = a 1 3 w 11 4 + a 2 3 w 12 4 + a 3 3 w 13 4 + a 4 3 w 13 4 a_1^4=\sigma(z_1^4) 而z_1^4=a_1^3w_{11}^4+a_2^3w_{12}^4+a_3^3w_{13}^4+a_4^3w_{13}^4 a14=σ(z14)而z14=a13w114+a23w124+a33w134+a43w134所以,
∂ a 1 4 ∂ w 11 2 = ∂ a 1 4 ∂ z 1 4 ( ∂ a 1 3 w 11 4 ∂ w 11 2 + ∂ a 2 3 w 12 4 ∂ w 11 2 + ∂ a 3 3 w 13 4 ∂ w 11 2 + ∂ a 4 3 w 13 4 ∂ w 11 2 ) \frac{\partial a_1^4}{\partial w_{11}^{2}} =\frac{\partial a_1^4}{\partial z_{1}^{4}} ( \textcolor{red}{ \frac{\partial a_1^3w_{11}^4}{\partial w_{11}^{2}} } + \frac{\partial a_2^3w_{12}^4}{\partial w_{11}^{2}} + \frac{\partial a_3^3w_{13}^4}{\partial w_{11}^{2}} + \frac{\partial a_4^3w_{13}^4}{\partial w_{11}^{2}} ) ∂w112∂a14=∂z14∂a14(∂w112∂a13w114+∂w112∂a23w124+∂w112∂a33w134+∂w112∂a43w134)
好,我们继续往下推,上式中红色部分:
∂ a 1 3 w 11 4 ∂ w 11 2 = w 11 4 ∂ a 1 3 ∂ z 1 3 ( ∂ a 1 2 w 11 3 ∂ w 11 2 + ∂ a 2 2 w 12 3 ∂ w 11 2 + ∂ a 3 2 w 13 4 ∂ w 13 3 ) \frac{\partial a_1^3w_{11}^4}{\partial w_{11}^{2}} \\ = w_{11}^4 \frac{\partial a_1^3}{\partial z_1^3} ( \frac{\partial a_1^2w_{11}^3}{\partial w_{11}^{2}} + \frac{\partial a_2^2w_{12}^3}{\partial w_{11}^{2}} + \frac{\partial a_3^2w_{13}^4}{\partial w_{13}^{3}} ) ∂w112∂a13w114=w114∂z13∂a13(∂w112∂a12w113+∂w112∂a22w123+∂w133∂a32w134)
此时我们发现,
∂ a 2 2 w 12 3 ∂ w 11 2 和 ∂ a 3 2 w 13 4 ∂ w 13 3 都 不 是 w 11 2 的 函 数 , 所 以 都 为 0 \textcolor{red}{ \frac{\partial a_2^2w_{12}^3}{\partial w_{11}^{2}}和\frac{\partial a_3^2w_{13}^4}{\partial w_{13}^{3}}都不是w_{11}^2的函数,所以都为0 } ∂w112∂a22w123和∂w133∂a32w134都不是w112的函数,所以都为0
于是,
∂ a 1 3 w 11 4 ∂ w 11 2 = w 11 4 ∂ a 1 3 ∂ z 1 3 ( ∂ a 1 2 w 11 3 ∂ w 11 2 ) \frac{\partial a_1^3w_{11}^4}{\partial w_{11}^{2}} \\ = w_{11}^4 \frac{\partial a_1^3}{\partial z_1^3} ( \frac{\partial a_1^2w_{11}^3}{\partial w_{11}^{2}} ) ∂w112∂a13w114=w114∂z13∂a13(∂w112∂a12w113)
于是乎同理得,
∂ a 1 4 ∂ w 11 2 = ∂ a 1 4 ∂ z 1 4 ( ∂ a 1 3 w 11 4 ∂ w 11 2 + ∂ a 2 3 w 12 4 ∂ w 11 2 + ∂ a 3 3 w 13 4 ∂ w 11 2 + ∂ a 4 3 w 13 4 ∂ w 11 2 ) = ∂ a 1 4 ∂ z 1 4 ( w 11 4 ∂ a 1 3 ∂ z 1 3 ( ∂ a 1 2 w 11 3 ∂ w 11 2 ) + w 12 4 ∂ a 2 3 ∂ z 2 3 ( ∂ a 1 2 w 21 3 ∂ w 11 2 ) + w 13 4 ∂ a 3 3 ∂ z 3 3 ( ∂ a 1 2 w 31 3 ∂ w 11 2 ) + w 14 4 ∂ a 4 3 ∂ z 4 3 ( ∂ a 1 2 w 41 3 ∂ w 11 2 ) ) = ∂ a 1 4 ∂ z 1 4 ( w 11 4 ∂ a 1 3 ∂ z 1 3 ( w 11 3 x 1 ) + w 12 4 ∂ a 2 3 ∂ z 2 3 ( w 21 3 x 1 ) + w 13 4 ∂ a 3 3 ∂ z 3 3 ( w 31 3 x 1 ) + w 14 4 ∂ a 4 3 ∂ z 4 3 ( w 41 3 x 1 ) ) = A \frac{\partial a_1^4}{\partial w_{11}^{2}} =\frac{\partial a_1^4}{\partial z_{1}^{4}} ( \frac{\partial a_1^3w_{11}^4}{\partial w_{11}^{2}} + \frac{\partial a_2^3w_{12}^4}{\partial w_{11}^{2}} + \frac{\partial a_3^3w_{13}^4}{\partial w_{11}^{2}} + \frac{\partial a_4^3w_{13}^4}{\partial w_{11}^{2}} ) \\= \frac{\partial a_1^4}{\partial z_{1}^{4}} (w_{11}^4 \frac{\partial a_1^3}{\partial z_1^3} ( \frac{\partial a_1^2w_{11}^3}{\partial w_{11}^{2}} ) +w_{12}^4 \frac{\partial a_2^3}{\partial z_2^3} ( \frac{\partial a_1^2w_{21}^3}{\partial w_{11}^{2}} ) +w_{13}^4 \frac{\partial a_3^3}{\partial z_3^3} ( \frac{\partial a_1^2w_{31}^3}{\partial w_{11}^{2}} ) +w_{14}^4 \frac{\partial a_4^3}{\partial z_4^3} ( \frac{\partial a_1^2w_{41}^3}{\partial w_{11}^{2}} ) ) \\= \frac{\partial a_1^4}{\partial z_{1}^{4}} (w_{11}^4 \frac{\partial a_1^3}{\partial z_1^3} ( w_{11}^{3} x_1 ) +w_{12}^4 \frac{\partial a_2^3}{\partial z_2^3} ( w_{21}^{3} x_1 ) +w_{13}^4 \frac{\partial a_3^3}{\partial z_3^3} ( w_{31}^{3} x_1 ) +w_{14}^4 \frac{\partial a_4^3}{\partial z_4^3} ( w_{41}^{3} x_1 ) )\\=\textcolor{red}{A} ∂w112∂a14=∂z14∂a14(∂w112∂a13w114+∂w112∂a23w124+∂w112∂a33w134+∂w112∂a43w134)=∂z14∂a14(w114∂z13∂a13(∂w112∂a12w113)+w124∂z23∂a23(∂w112∂a12w213)+w134∂z33∂a33(∂w112∂a12w313)+w144∂z43∂a43(∂w112∂a12w413))=∂z14∂a14(w114∂z13∂a13(w113x1)+w124∂z23∂a23(w213x1)+w134∂z33∂a33(w313x1)+w144∂z43∂a43(w413x1))=A
∂ a 2 4 ∂ w 11 2 = ∂ a 1 4 ∂ z 1 4 ( w 21 4 ∂ a 1 3 ∂ z 1 3 ( w 11 3 x 1 ) + w 22 4 ∂ a 2 3 ∂ z 2 3 ( w 21 3 x 1 ) + w 23 4 ∂ a 3 3 ∂ z 3 3 ( w 31 3 x 1 ) + w 24 4 ∂ a 4 3 ∂ z 4 3 ( w 41 3 x 1 ) ) = B \frac{\partial a_2^4}{\partial w_{11}^{2}}= \frac{\partial a_1^4}{\partial z_{1}^{4}} (w_{21}^4 \frac{\partial a_1^3}{\partial z_1^3} ( w_{11}^{3} x_1 ) +w_{22}^4 \frac{\partial a_2^3}{\partial z_2^3} ( w_{21}^{3} x_1 ) +w_{23}^4 \frac{\partial a_3^3}{\partial z_3^3} ( w_{31}^{3} x_1 ) +w_{24}^4 \frac{\partial a_4^3}{\partial z_4^3} ( w_{41}^{3} x_1 ) )\\=\textcolor{red}{B} ∂w112∂a24=∂z14∂a14(w214∂z13∂a13(w113x1)+w224∂z23∂a23(w213x1)+w234∂z33∂a33(w313x1)+w244∂z43∂a43(w413x1))=B
最后,
∂ C ∂ w 11 2 = ∂ C ∂ a 1 4 ∂ a 1 4 ∂ w 11 2 + ∂ C ∂ a 2 4 ∂ a 2 4 ∂ w 11 2 = ∂ C ∂ a 1 4 A + ∂ C ∂ a 2 4 B \frac{\partial C}{\partial w_{11}^{2}} = \frac{\partial C}{\partial a_1^4} \frac{\partial a_1^4}{\partial w_{11}^{2}} + \frac{\partial C}{\partial a_2^4} \frac{\partial a_2^4}{\partial w_{11}^{2}} \\ = \frac{\partial C}{\partial a_1^4} \textcolor{red} {A} \\+ \frac{\partial C}{\partial a_2^4} \textcolor{red} {B} ∂w112∂C=∂a14∂C∂w112∂a14+∂a24∂C∂w112∂a24=∂a14∂CA+∂a24∂CB
至此,这个问题就基本清楚了.
我们看到,正向计算的时候每计算一个 ∂ C ∂ w j k l \frac{\partial C}{\partial w_{jk}^l} ∂wjkl∂C都要把 w j k l 到 C w_{jk}^l到C wjkl到C所有路径上的local偏导数进行计算一遍,全连接的深度神经网络的链接数量是以亿计的,像这样每求一个梯度都要把几亿个路径算一遍是非常耗时耗力的.可从上面的推导可以看到, A \textcolor{red}{A} A和 B \textcolor{red}{B} B中很多计算有重复,那有没有一种方法能把这些重复的计算事先算好然后简单的通过前后层的关系就能计算出梯度呢?这样就不必搜索所有的相关路径计算了.
有,那就是BP. 当然BP只是一个求偏导的数学技巧,是方法不是目的。
有了梯度之后,我们只要知道学习率 η \eta η,然后把所有的 w j k l − η ∗ ∂ C ∂ w j k l w_{jk}^l-\eta*\frac{\partial C}{\partial w_{jk}^l} wjkl−η∗∂wjkl∂C就得到了一组新的权重。(梯度是函数最快上升的方向,所以这边是减号,最快下降的方向。
)这组权重必然会使 C C C减小,反复如此,直到学习到 ∂ C ∂ w j k l \frac{\partial C}{\partial w_{jk}^l} ∂wjkl∂C都趋近于0了,理论上就是到了一个局部的底,权重的学习也就减缓直至不再变化了。如此就完成了网络的学习。
5.BP推导
1) 我们令
δ j l = ∂ C ∂ z j l \delta_j^l=\frac{\partial C}{\partial z_j^l} δjl=∂zjl∂C
**称作BP误差,Error , BP的精髓就是它 **
2) 则最后一层的误差:
δ j L = ∂ C ∂ z j L \delta_j^L=\frac{\partial C}{\partial z_j^L} δjL=∂zjL∂C
由于:
a j L = σ ( z j L + b j L ) a_j^L=\sigma(z_j^L+b_j^L) ajL=σ(zjL+bjL)
根据链式法则:
δ j L = ∂ C ∂ a j L ∂ a j L ∂ z j L = ∂ C ∂ a j L σ ′ ( z j L ) (1) \delta_j^L=\frac{\partial C}{\partial a_j^L} \frac{\partial a_j^L}{\partial z_j^L}=\frac{\partial C}{\partial a_j^L} \sigma'(z_j^L) \space\space\textbf{(1)} δjL=∂ajL∂C∂zjL∂ajL=∂ajL∂Cσ′(zjL) (1)
3) 由于
δ j l = ∂ C ∂ z j l = ∑ k ∂ C ∂ z k l + 1 ∂ z k l + 1 ∂ z j l \delta_j^l= \frac{\partial C}{\partial z_j^l} \\ \qquad \qquad \qquad = \sum_k \frac{\partial C}{\partial z_k^{l+1}} \frac{\partial z_k^{l+1}}{\partial z_j^l} δjl=∂zjl∂C=k∑∂zkl+1∂C∂zjl∂zkl+1
(上式需要细细品味一下,特别是为什么需要 ∑ k \sum_k ∑k符号,主要是要包含被 w w w影响的所有路径)
并且
δ j l + 1 = ∂ C ∂ z j l + 1 \delta_j^{l+1}=\frac{\partial C}{\partial z_j^{l+1}} δjl+1=∂zjl+1∂C
则:
δ j l = ∑ k ∂ z k l + 1 ∂ z j l δ k l + 1 (2) \delta_j^l=\sum_k \frac{\partial z_k^{l+1}}{\partial z_j^l} \delta_k^{l+1} \space\space\textbf{(2)} δjl=k∑∂zjl∂zkl+1δkl+1 (2)
至此,前一层和后一层的误差的关系已然浮出水面
4) 接下来来看我们最关心的 C 对 w C对w C对w的梯度 ∂ C ∂ w j k l \frac{\partial C}{\partial w_{jk}^l} ∂wjkl∂C以及C对bias的梯度 ∂ C ∂ b j l \frac{\partial C}{\partial b_j^l} ∂bjl∂C
由于
z j l = ∑ k w j k l a k l − 1 + b j l z_j^l=\sum_k w_{jk}^la_k^{l-1}+b_j^l zjl=k∑wjklakl−1+bjl
则
∂ C ∂ w j k l = ∂ C ∂ z j l ∂ z j l ∂ w j k l = δ j l a k l − 1 (3) \frac{\partial C}{\partial w_{jk}^l}=\frac{\partial C}{\partial z_j^l}\frac{\partial z_j^l}{\partial w_{jk}^{l}} \\ \space \\= \delta_j^la_k^{l-1} \space\space\textbf{(3)} ∂wjkl∂C=∂zjl∂C∂wjkl∂zjl =δjlakl−1 (3)
∂ C ∂ b j l = ∂ C ∂ z j l ∂ z j l ∂ b j l = δ j l ∗ 1 = δ j l (4) \frac{\partial C}{\partial b_j^l} = \frac{\partial C}{\partial z_j^l}\frac{\partial z_j^l}{\partial b_{j}^{l}} \\ \space \\= \delta_j^l *1 = \delta_j^l \space\space\textbf{(4)} ∂bjl∂C=∂zjl∂C∂bjl∂zjl =δjl∗1=δjl (4)
至此,我们获得了 ( 1 ) ( 2 ) ( 3 ) ( 4 ) (1)(2)(3)(4) (1)(2)(3)(4)四个BP的公式,证毕。
6.总结一下
当我们有
δ j L = ∂ C ∂ a j L σ ′ ( z j L ) (1) \delta_j^L=\frac{\partial C}{\partial a_j^L} \sigma'(z_j^L) \space\space\textbf{(1)} δjL=∂ajL∂Cσ′(zjL) (1)
δ j l = ∑ k ∂ z k l + 1 ∂ z j l δ k l + 1 (2) \delta_j^l=\sum_k \frac{\partial z_k^{l+1}}{\partial z_j^l} \delta_k^{l+1} \space\space\textbf{(2)} δjl=k∑∂zjl∂zkl+1δkl+1 (2)
∂ C ∂ w j k l = δ j l a k l − 1 (3) \frac{\partial C}{\partial w_{jk}^l}= \delta_j^la_k^{l-1} \space\space\textbf{(3)} ∂wjkl∂C=δjlakl−1 (3)
∂ C ∂ b j l = δ j l ∗ 1 = δ j l (4) \frac{\partial C}{\partial b_j^l} = \delta_j^l *1 = \delta_j^l \space\space\textbf{(4)} ∂bjl∂C=δjl∗1=δjl (4)
又由于损失函数:
C = 1 2 ∥ y − a L ∥ 2 = 1 2 ∑ j ( y j − a j L ) 2 C=\frac{1}{2}\|y-a^L\|^2=\frac{1}{2} \sum_j (y_j-a_j^L)^2 C=21∥y−aL∥2=21j∑(yj−ajL)2
所以
∂ C ∂ a j L = ( y j − a j L ) \frac{\partial C}{\partial a_j^L} = (y_j-a_j^L) ∂ajL∂C=(yj−ajL)
我们发现所有等号右边的值都可求解了,最神奇的是梯度只和误差还有前一层的输出有关,不必去计算所有路径了,而且对于一次梯度下降,每个神经元的 δ \delta δ都只需要计算一遍,存下来计算其他节点直接可以用,复杂度极大降低,至此我们就彻底搞明白了为什么要用BP以及BP是怎样推导的。