人工智能---反向传播的原理和理论以及softmax-with-loss层作为反向传播起点的实现
系列文章目录
人工智能—神经网络激活函数恒等函数、sigmoid函数、softmax函数详解
文章目录
- 系列文章目录
- 前言
- 一、什么是反向传播?
- 二、反向传播的原理
- 三、反向传播的应用
-
- 1.反向传播示意图
- 2.反向传播的两种结点情况
-
- 1)加法结点
- 2)乘法结点
- 3)log结点
- 四、softmax-with-loss层反向传播实现
-
- 1.小节前言
- 2.softmax-with-loss层介绍
- 3.softmax-with-loss层图示
- 4.softmax-with-loss层反向传播
- 五、代码的实现
-
- 1.乘法层
- 2.加法层
- 3.softmax-with-loss层
- 总结
前言
我们已经在前面几章的内容中充分学习了神经网络的结构特点以及实现了简单的网络结构,但神经网络的神奇之处在于他的学习能力已经预测能力,而其中的预测原理我们已经讲过,剩下的就是最关键也是最复杂的学习能力的实现了,这章笔者就会带领大家进行神经网络反向传播的学习。
一、什么是反向传播?
我们在前一章中学会了梯度的概念,知道了梯度是指导权重更新的指标,但其实梯度的原理虽然简单,但计算量在结点数量多了后会变的异常的复杂和困难,因为你需要对每一个结点进行微分的计算,于是我们提出了反向传播这一更加快捷的梯度计算方法。所以简单的说反向传播就是一种快速计算所有结点微分的方法。
二、反向传播的原理
反向传播其实是基于链式法则,链式法则的定义可能比较晦涩——如果一个函数是复合函数,那这个复合函数的导数可以由构成这个函数的各个函数的导数乘积构成。
举个例子:
z = t 2 z = t^2 z=t2
t = x + y t=x+y t=x+y
∂ z ∂ x = ∂ z ∂ t / ∗ ∂ t / ∂ x \frac{\partial z}{\partial x}=\frac{\partial z}{\partial t\mkern-11mu/}{*}\frac{\partial t\mkern-11mu/}{\partial x} ∂x∂z=∂t/∂z∗∂x∂t/
∵ ∂ z ∂ t = 2 t , ∂ t ∂ x = 1 ∴ ∂ z ∂ x = 2 t \because\frac{\partial z}{\partial t}=2t,\frac{\partial t}{\partial x}=1\therefore\frac{\partial z}{\partial x}=2t ∵∂t∂z=2t,∂x∂t=1∴∂x∂z=2t
∵ t = x + y ∴ ∂ z ∂ x = 2 t = 2 ( x + y ) \because t=x+y\therefore \frac{\partial z}{\partial x}=2t=2(x+y) ∵t=x+y∴∂x∂z=2t=2(x+y)
那链式法则我们看懂了,可是他和反向传播又是什么关系呢,他又是如何加快求微分速度的呢?
三、反向传播的应用
1.反向传播示意图
我们可以参考之前的神经网络拓扑图

每一个结点都需要我们进行梯度计算,如果用平常的计算方法,每一次我们都独立的计算 ∂ z ∂ x \frac{\partial z}{\partial x} ∂x∂z的值,就会变的很麻烦,而通过链式法则的反向传播使我们每次都只需要依据上一步的微分结果结合当前神经元的计算方式进行一次简单的微分计算即可。
2.反向传播的两种结点情况
上面我们介绍了反向传播的整体视图,下面将具体结合加法和乘法两种结点进行介绍细节的框架
1)加法结点
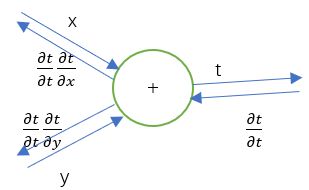
我们以 t = x + y t = x+y t=x+y为例:
∵ ∂ t ∂ x = 1 , ∂ t ∂ y = 1 \because \frac{\partial t}{\partial x}=1,\frac{\partial t}{\partial y}=1 ∵∂x∂t=1,∂y∂t=1
∴ ∂ t ∂ t ∗ ∂ t ∂ x = ∂ t ∂ t , ∂ t ∂ t ∗ ∂ t ∂ y = ∂ t ∂ t \therefore \frac{\partial t}{\partial t}*\frac{\partial t}{\partial x}=\frac{\partial t}{\partial t},\frac{\partial t}{\partial t}*\frac{\partial t}{\partial y}=\frac{\partial t}{\partial t} ∴∂t∂t∗∂x∂t=∂t∂t,∂t∂t∗∂y∂t=∂t∂t
所以综上所述,加法结点从前方传导来的微分会在几个加法分支这原封不动的往下传播。
2)乘法结点
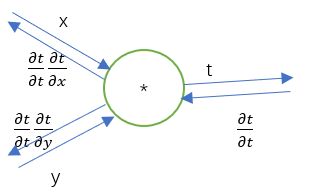
我们还是举一个简单的例子: t = x y t=xy t=xy
∵ ∂ t ∂ x = y , ∂ t ∂ y = x \because \frac{\partial t}{\partial x}=y,\frac{\partial t}{\partial y}=x ∵∂x∂t=y,∂y∂t=x
∴ ∂ t ∂ t ∗ ∂ t ∂ x = ∂ t ∂ t ∗ y , ∂ t ∂ t ∗ ∂ t ∂ y = ∂ t ∂ t ∗ x \therefore \frac{\partial t}{\partial t}*\frac{\partial t}{\partial x}=\frac{\partial t}{\partial t}*y,\frac{\partial t}{\partial t}*\frac{\partial t}{\partial y}=\frac{\partial t}{\partial t}*x ∴∂t∂t∗∂x∂t=∂t∂t∗y,∂t∂t∗∂y∂t=∂t∂t∗x
所以综上所述,乘法结点从前方传导来的微分会在乘法分支这与对换的x,y臂进行相乘。
3)log结点
以 y = l o g x y=logx y=logx为例:
∂ y ∂ x = 1 x \frac{\partial y}{\partial x}=\frac 1x ∂x∂y=x1
四、softmax-with-loss层反向传播实现
1.小节前言
在经过上面几个小节的简单介绍后,大家其实对反向传播的原理应该掌握了,接下来就是实践的过程了,大家可以根据前面所学的自行搭建一个网络拓扑图,进行反向传播的实验。
我这边会带领大家进行最常用的softmax-with-loss层的反向传播实现,但这个层比较复杂,如果感觉有困难的同学,可以看到前面的原理就够了。
2.softmax-with-loss层介绍
softmax-with-loss层听着陌生,但他其实是前面我们讲过的两个算法的组合罢了,即:Softmax和Cross Entropy Error的一个组合。
这样组合的意义是既能输出softmax的一个预测结果,又能根据softmax的预测结果和实际结果在Cross Entropy Error中进行一个损失值的计算。
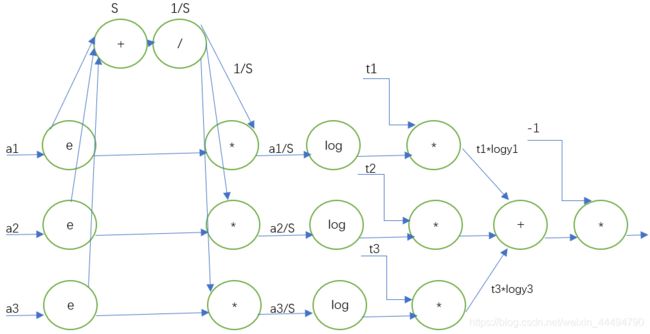
3.softmax-with-loss层图示
softmax当时我们已经学过,定义式为:
y k = e a k ∑ i = 0 n e a i y_k=\frac{e^{a_k}}{\sum_{i=0}^ne^{a_i}} yk=∑i=0neaieak
Cross Entropy Error的定义式为:
L = − ∑ k t k log y k L=-\sum_kt_k\log y_k L=−k∑tklogyk
softmax中的 a i a_i ai来自上一个网络层的输出,而Cross Entropy Error的 y k y_k yk来自softmax层的输出, t k t_k tk来自监督标签。
于是根据上面的定义式,为了方便我们后面更加直观的进行反向传播,我们可以画出softmax-with-loss层的拓扑图。
4.softmax-with-loss层反向传播
反向传播的起点,便是我们的softmax-with-loss层的终点,也就是输出 L L L.
第一步对 L L L求微分得: ∂ L ∂ L = 1 \frac{\partial L}{\partial L} =1 ∂L∂L=1
然后经过第一个乘法结点,根据乘法结点定则可得,向加法结点传播的这条路径的微分为:
∂ L ∂ L ∗ ( − 1 ) = − 1 \frac{\partial L}{\partial L}*(-1)=-1 ∂L∂L∗(−1)=−1
然后经过一个三路径的加法结点,根据加法的定则可得,将前面的微分原封不动的传播下去,所以:
t i ∗ l o g y i ← = − 1 \underleftarrow {t_i*logy_i}=-1 ti∗logyi=−1
然后顺着 t i ∗ l o g y i ← \underleftarrow {t_i*logy_i} ti∗logyi进入三个乘法结点,再根据乘法法则可得 l o g a i S ← \underleftarrow {log\frac {a_i}S} logSai这条路径的值为-1和臂 t i t_i ti的乘积。
l o g e a i S ← = − 1 ∗ t i = − t i \underleftarrow {log\frac {e^{a_i}}S}=-1*t_i=-t_i logSeai=−1∗ti=−ti
再经过log结点可得:
− t i e a i / S -\frac{t_i}{e^{a_i}/S} −eai/Sti
到这里其实Cross Entropy Error的反向传播已经完成了,但由于他和softmax是首尾相接的,所以他的反向传播的终点也就是softmax反向传播的起点。所以softmax的反向传播开始值为:
− t i e a i / S -\frac{t_i}{e^{a_i}/S} −eai/Sti
但softmax分为两层传播路径,我们先看上面的那一层,也就是求和的那一层。
先是乘法结点将 − t i e a i / S -\frac{t_i}{e^{a_i}/S} −eai/Sti与第一层的臂相乘:
− t i e a i / S ∗ e a i = − S t i -\frac{t_i}{e^{a_i}/S}*e^{a_i}=-St_i −eai/Sti∗eai=−Sti
反向传播的过程中难免会遇到分支,而面对分支情况,反向传播会对分支进行一个求和的操作,看我们紧接着的这个结点例子:
( − t 1 S , − t 2 S , − t 3 S ) (-t_1S,-t_2S,-t_3S) (−t1S,−t2S,−t3S)
他们曾经是因为经历了一个除法结点后分散,所以会在这汇聚,即为:
− S ( t 1 + t 2 + t 3 ) -S(t_1+t_2+t_3) −S(t1+t2+t3)
再通过除法结点求微分可得:
− ( t 1 + t 2 + t 3 ) S -\frac {(t_1+t_2+t_3)}S −S(t1+t2+t3)
虽然这个就是我们结点的一个理论输出值了,但有时候我们不能只关注符号,也要关注符号的实际意义,让我们来想一下这个 t i t_i ti是什么?他是我们的监督标签,什么是监督标签,他是一个one-hot矩阵,也就是表示了正确答案为1,其他都是0,那么 t i t_i ti的和是不是就是1呢?所以:
− ( t 1 + t 2 + t 3 ) S = − 1 S -\frac {(t_1+t_2+t_3)}S=-\frac 1S −S(t1+t2+t3)=−S1
这一步大家可能很难想到,但这考验了你们对每个数据流的实际意义的把握。
然后是通过一个加法结点,保持原样:
− 1 S -\frac {1}S −S1
但到这里我们又遇到一个分支结点,也就是e结点,这就需要我们将另一条边的微分求出来。
那就退回原来的乘法结点处,这次我们需要将 − t i y i -\frac {t_i}{y_i} −yiti乘以他的另一条臂了:
− t i y i ∗ 1 S -\frac {t_i}{y_i}*\frac 1S −yiti∗S1
∵ y i = e a i S \because y_i = \frac{e^{a_i}}{S} ∵yi=Seai
∴ − t i y i ∗ 1 S = − t i e a i \therefore -\frac {t_i}{y_i}*\frac 1S=-\frac{t_i}{e^{a_i}} ∴−yiti∗S1=−eaiti
然后是 e e e结点的求和,和前面的/号结点其实类似:
e ( a i ) → ( 1 S − t i e a i ) e a i e(a_i) \to (\frac 1S-\frac{t_i}{e^{a_i}})e^{a_i} e(ai)→(S1−eaiti)eai
∴ e ( a i ) → y i − t i \therefore e(a_i) \to y_i-t_i ∴e(ai)→yi−ti
到这里我们的softmax的反向传播也结束了,对应我们当时三个输入 a i a_i ai我们可以验证到我们的反向传播的输入也是三个,分别是:
{ y 1 − t 1 y 2 − t 2 y 3 − t 3 \left\{ \begin{array}{c} y1-t1\\ y2-t2\\ y3-t3 \end{array} \right. ⎩⎨⎧y1−t1y2−t2y3−t3
那我们就已知第 i i i个分类的前向输入是 a i a_i ai,反向输入为: y i − t i y_i-t_i yi−ti
我们这次采用的是一个三分类的示例,为了证明更加快捷和简洁,如果直接使用通式代入进行证明可能会显得很复杂,当然感兴趣的读者可以再私下进行扩展到n项进行证明,相信一定也能得出同样的结论。
五、代码的实现
1.乘法层
x = None
y = None
def backward(dout):
dx,dy = dout * y,dout*x
return dx,dy
2.加法层
def backward(dout):
return dout,dout
3.softmax-with-loss层
batch_size = None
t = None
y = None
def backward(dout = 1):
return (y-t)/batch_size
总结
到这里我们对反向传播的介绍也已经全部结束了,结合上一章中梯度的知识和反向传播的这个工具,相信大家已经可以实现一个“活”的神经网络了!接下来我可能会给大家带来的就更多的是实例的讲解了。