C++手工实现BP神经网络用于MNIST手写数字识别
第一次写机器学习的文章。学完反向传播(BP算法)后做一个小实验来巩固一下,从最基本的实现到最后的优化,实验过程中遇到很多坑,比如超参数的设定,比如每种任务适合的输出函数和相应的损失函数。一度因为选择不恰当的学习率,神经元数目和激活函数而训练出人工智障。代码采用纯C/C++完成,未采用向量运算。本文不过多讨论算法原理方面内容,主要用于记录实验过程。
一. 在实现手写数字识别之前,先练习一个小任务,用神经网络学习最简单的a+b规则。
搭建如图所示的神经网络,学习计算两个数的和,所以输入层的节点数为2,设置隐藏层的神经元数目为40,激活函数为Sigmod函数,输出层为单个神经元。因为这是一个用神经网络解决回归问题的任务,输出层节点的激活函数可以使用阶跃函数,也可以不设置。为了方便起见未设置激励函数,即y=f(![]() X+b)=
X+b)=![]() X+b。
X+b。
当然也可以用于拟合非线性方程,理论上足够数量的神经元可以拟合任意实数范围内的方程。
当神经网络用于分类问题时,输出层可以采取补不同的激活函数。
Sigmod函数可用于二分类问题,Softmax函数可用于多分类问题。
BP算法基于链式求导法则,下面仅给出BP算法的相关公式,不予证明:
代价函数采用输出层的误差平方:![]() ,t代表标准输出,y代表预测值
,t代表标准输出,y代表预测值
用随机梯度下降算法进行权重的更新:![]()
此外,对数据进行归一化的处理,将数据处理到0~1的范围内,否则可能出现收敛过慢或无法收敛的情况。
#include
#define in 2
#define out 1
#define hide 40
using namespace std ;
double a[2*hide];//隐藏层输出
double y=0;//输出层输出
double w1[2*hide][2*hide],b1[2*hide];//隐藏层权重
double w2[2*hide][2*hide],b2=0;//输出层权重
double delta,delta1[2*hide];//误差项
double x[1010][3];//数据集
double label[1010];//标签
double maxx=0,maxs=0;
double f(double x)
{
return 1.0/(1.0+exp(-x));
}
void data()
{
for(int i=0;i<1000;i++)
{
x[i][0]=rand()%10000;
x[i][1]=rand()%10000;
label[i]=x[i][0]+x[i][1];
}
for(int i=0;i<1000;i++)
{
x[i][2]=1.0;
x[i][0]/=10000;
x[i][1]/=10000;
label[i]/=20000;
}
}
void Network()
{
memset(a,0,sizeof(a));
memset(b1,0,sizeof(b1));
/*freopen("out.txt","r",stdin);
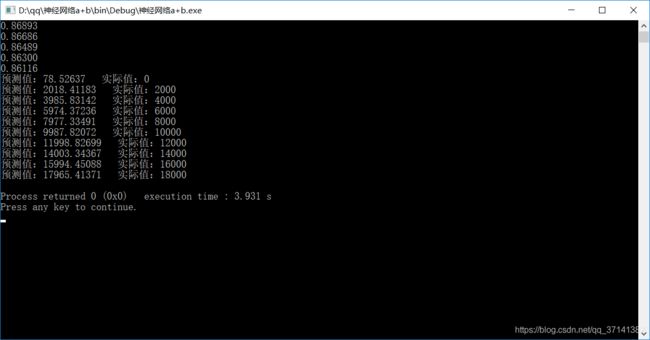
for(int i=0;i 实验结果:
二. MNIST手写数字识别实战
MNIST数据集为大小为28*28*3的图像,输入神经元有784个,输出层为10个神经元。此任务为一个多分类任务,所以我们采用softmax函数作为输出层的激励函数,权重更新方法会在稍后给出。在不设置隐藏层的情况下,训练几分钟后的神经网络在测试集上达到88%左右的准确率。
softmax的输出为属于各个标签的概率,交叉熵损失函数基于多项式分布确定,此处不多做讨论。
softmax采用交叉熵作为损失函数
交叉熵损失函数:![]() 。计算梯度为:
。计算梯度为:![]()
利用梯度下降算法求解即可。
同样的将图像进行归一化处理,使每个像素点归一化到0~1的范围之内。
使用softmax函数时出现溢出情况,可以采取的方法是将所有输出值减去最大值,可同时避免上溢出和下溢出。
#include
#define in 784
#define out 10
using namespace std ;
double data_out[50];//输出层输出
double w[50][1000],b[50];//输出层权重
double delta[50];//误差项
vectorlabels;
vector >images;//训练集
vectorlabels1;
vector >images1;//测试集
void test();
int ReverseInt(int i)
{
unsigned char ch1, ch2, ch3, ch4;
ch1 = i & 255;
ch2 = (i >> 8) & 255;
ch3 = (i >> 16) & 255;
ch4 = (i >> 24) & 255;
return((int)ch1 << 24) + ((int)ch2 << 16) + ((int)ch3 << 8) + ch4;
}
void read_Mnist_Label(string filename, vector&labels)
{
ifstream file;
file.open("train-labels.idx1-ubyte", ios::binary);
if (file.is_open())
{
int magic_number = 0;
int number_of_images = 0;
file.read((char*)&magic_number, sizeof(magic_number));
file.read((char*)&number_of_images, sizeof(number_of_images));
magic_number = ReverseInt(magic_number);
number_of_images = ReverseInt(number_of_images);
cout << "magic number = " << magic_number << endl;
cout << "number of images = " << number_of_images << endl;
for (int i = 0; i < number_of_images; i++)
{
unsigned char label = 0;
file.read((char*)&label, sizeof(label));
labels.push_back((double)label);
}
}
}
void read_Mnist_Images(string filename, vector >&images)
{
ifstream file("train-images.idx3-ubyte", ios::binary);
if (file.is_open())
{
int magic_number = 0;
int number_of_images = 0;
int n_rows = 0;
int n_cols = 0;
unsigned char label;
file.read((char*)&magic_number, sizeof(magic_number));
file.read((char*)&number_of_images, sizeof(number_of_images));
file.read((char*)&n_rows, sizeof(n_rows));
file.read((char*)&n_cols, sizeof(n_cols));
magic_number = ReverseInt(magic_number);
number_of_images = ReverseInt(number_of_images);
n_rows = ReverseInt(n_rows);
n_cols = ReverseInt(n_cols);
cout << "magic number = " << magic_number << endl;
cout << "number of images = " << number_of_images << endl;
cout << "rows = " << n_rows << endl;
cout << "cols = " << n_cols << endl;
for (int i = 0; i < number_of_images; i++)
{
vectortp;
for (int r = 0; r < n_rows; r++)
{
for (int c = 0; c < n_cols; c++)
{
unsigned char image = 0;
file.read((char*)&image, sizeof(image));
tp.push_back(image);
}
}
images.push_back(tp);
}
}
}
void read_Mnist_Label1(string filename, vector&labels)
{
ifstream file;
file.open("t10k-labels.idx1-ubyte", ios::binary);
if (file.is_open())
{
int magic_number = 0;
int number_of_images = 0;
file.read((char*)&magic_number, sizeof(magic_number));
file.read((char*)&number_of_images, sizeof(number_of_images));
magic_number = ReverseInt(magic_number);
number_of_images = ReverseInt(number_of_images);
for (int i = 0; i < number_of_images; i++)
{
unsigned char label = 0;
file.read((char*)&label, sizeof(label));
labels.push_back((double)label);
}
}
}
void read_Mnist_Images1(string filename, vector >&images)
{
ifstream file("t10k-images.idx3-ubyte", ios::binary);
if (file.is_open())
{
int magic_number = 0;
int number_of_images = 0;
int n_rows = 0;
int n_cols = 0;
unsigned char label;
file.read((char*)&magic_number, sizeof(magic_number));
file.read((char*)&number_of_images, sizeof(number_of_images));
file.read((char*)&n_rows, sizeof(n_rows));
file.read((char*)&n_cols, sizeof(n_cols));
magic_number = ReverseInt(magic_number);
number_of_images = ReverseInt(number_of_images);
n_rows = ReverseInt(n_rows);
n_cols = ReverseInt(n_cols);
for (int i = 0; i < number_of_images; i++)
{
vectortp;
for (int r = 0; r < n_rows; r++)
{
for (int c = 0; c < n_cols; c++)
{
unsigned char image = 0;
file.read((char*)&image, sizeof(image));
tp.push_back(image);
}
}
images.push_back(tp);
}
}
}
void softmax(double data_out[])
{
double sum=0.0;
for(int i=0;isign)
{
sign=data_out[i];
ans=i;
}
}
return ans;
}
void bp(int t)
{
for(int i=0;i
可以进行优化的几点想法:
1.添加隐藏层可以增强神经网络的拟合能力,当然相应的会增加计算的消耗。
2.可以采用dropout,增强模型的鲁棒性,避免过拟合。
引用:
https://blog.csdn.net/yiranlun3/article/details/78632752
https://www.zybuluo.com/hanbingtao/note/476663
https://blog.csdn.net/x_iya/article/details/53052963