多分类问题《PyTorch深度学习实践》
多分类
softmax分类器
输出变为多个
1.概率>0
2.概率和为1
1.softmax分类器,使用SoftMax分类器进行多分类问题

2.NLLLoss(nagative log likelihood loss ): Y是原始标签,另一个输入是 softmax 后 求对数
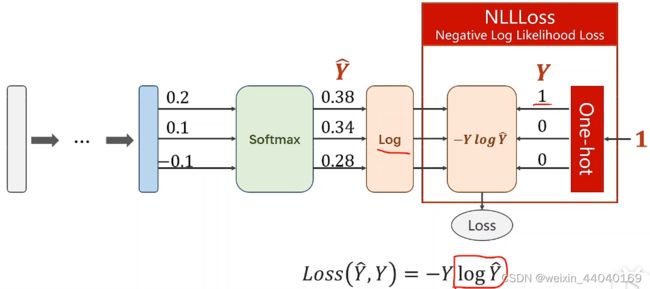
3.CrossEntropyLoss <==> LogSoftmax + NLLLoss
(One-hot独热编码 是一行或一列只有一位是1的矩阵)

import torch
y = torch.LongTensor([0])#长整形张量
z = torch.Tensor([[0.2,0.2,-0.1]])
criterion = torch.nn.CrossEntropyLoss() #交叉熵损失全部封装
loss = criterion(z,y)#计算损失
print(loss)
4.transforms 对图像进行原始处理的工具
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))])
pillow:读进来图像
神经网络特点:希望输入的数据比较小,在正一到负一之间,最好是符合正态分布,对神经网络训练最有帮助。
transform把Pillow图像转换成Tensor,把0-255像素值转换成0-1,然后把维度2828变成12828(cw*h)【通道,宽,高】的张量,这个过程用transform中的totensor实现,normalize(mean均值,std标准差)变成0-1分布~给神经网络训练
5.归一化:摘自 深度学习-归一化
作用:
——用于数据预处理,对数据总体的数值进行再分配,避免微小但具有重要含义的小数值数据被吞噬。
——在实际训练中,归一化同样具有加快模型收敛的作用。
——不同的样本数据事实数据分布不同,评价指标有所不同,归一化可用于统一数据分布
——过小数值,易造成梯度为0,训练失败,使用归一化避免过小数值趋于0的隐患。
——神经网络在本质上是通过输出对事物的统计概率来进行训练与预测,归一化则能将各个数值规范在[0,1]的范围。
——减小数据中的特殊样本,避免特殊样本对训练带来的不良影响。
作用-总结:
1.避免数值过小的数据被忽略
2.统一输入样本数据的评价指标
实现思路:
——所有数据转化为[0,1]或者[-1,1]之间,取消数据间的数量级差别,减少数据数量级差异过大所带来的不良影响。
6.设计模型
输入维度(N,1,28,28):N个样本,每个样本是一维,2828的图像(n,c,w,h),为4阶张量(4个参数),但在神经网络中要求输入样本为矩阵(二阶张量),所以第一步把128*28的三阶张量变成一阶的向量,怎么变呢?把图片的每一行拼起来构成一行,每一行有784个元素
view(-1,784)把张量变成2阶张量(2个参数),矩阵784列,-1表示自动去算batchsize
经过view之后变成了(N,784)的矩阵
【(阶,维),(矩阵,二维张量),(张量,向量)】不是很明白这几个概念????QAQ
矩阵的形变其实就是二维张量的形变方法

import torch
from torchvision import transforms
from torchvision import datasets
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim
# prepare dataset
batch_size = 64 #Compose可以把[]对象变成pipline一样??,把图片转变成张量c*w*h
transform = transforms.Compose([transforms.ToTensor(), transforms.Normalize((0.1307,), (0.3081,))]) # 定义transform变换
# transforms.ToTensor() 转变为张量----标准化
# transforms.Normalize((0.1307,), (0.3081,)) ----归一化,均值和标准差
train_dataset = datasets.MNIST(root='../dataset/mnist/', train=True, download=True, transform=transform) #transform放到数据集中,以使拿到的数据直接进行transform处理
train_loader = DataLoader(train_dataset, shuffle=True, batch_size=batch_size)
test_dataset = datasets.MNIST(root='../dataset/mnist/', train=False, download=True, transform=transform)
test_loader = DataLoader(test_dataset, shuffle=False, batch_size=batch_size)
# design model using class
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.l1 = torch.nn.Linear(784, 512)
self.l2 = torch.nn.Linear(512, 256)
self.l3 = torch.nn.Linear(256, 128)
self.l4 = torch.nn.Linear(128, 64)
self.l5 = torch.nn.Linear(64, 10)
def forward(self, x): # 原来是 (n,1,28,28)---经过view之后变成了(N,784)的矩阵
x = x.view(-1, 784) # -1其实就是自动获取mini_batch
x = F.relu(self.l1(x))
x = F.relu(self.l2(x))
x = F.relu(self.l3(x))
x = F.relu(self.l4(x))
return self.l5(x) # 最后一层不做激活,不进行非线性变换
model = Net()
# construct loss and optimizer
criterion = torch.nn.CrossEntropyLoss() #交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5) #梯度下降,带冲量momentum=0.5(冲破局部最小值)
# training cycle forward, backward, update
#一轮循环封装成函数
def train(epoch):
running_loss = 0.0
for batch_idx, data in enumerate(train_loader, 0):
# 获得一个批次的数据和标签
inputs, target = data
optimizer.zero_grad() #每个minibatch结束,梯度清零
# 获得模型预测结果(64, 10)
outputs = model(inputs)
# 交叉熵代价函数outputs(64,10),target(64)
loss = criterion(outputs, target)
loss.backward()
optimizer.step()
running_loss += loss.item()
if batch_idx % 300 == 299:#每300次迭代输出
print('[%d, %5d] loss: %.3f' % (epoch+1, batch_idx+1, running_loss/300))
running_loss = 0.0
def test():
correct = 0
total = 0
with torch.no_grad(): # 不计算梯度
for data in test_loader:
images, labels = data
outputs = model(images) # outputs矩阵
#_是占个位 表示那里有值但用不着 _, predicted 最大值及其下标
_, predicted = torch.max(outputs.data, dim=1) # dim=1 列是第0个维度,行是第1个维度
total += labels.size(0) #labels.size即(n,1) 取labels.size(0)=n
correct += (predicted == labels).sum().item() # predicted == labels比较,真1,加0
print('accuracy on test set: %d %% ' % (100*correct/total))
if __name__ == '__main__':
for epoch in range(10):
train(epoch)
test()
注:
Tensor
_, predicted = torch.max(outputs.data, dim=1) # dim=1 列是第0个维度,行是第1个维度
其实,不用考虑“行列”的概念
[[0.1205, 0.1218],
[0.1326, 0.1112],
[0.1276, 0.1477],
[0.1228, 0.1192],
[0.1221, 0.1173],
[0.1243, 0.1268],
[0.1252, 0.1277],
[0.1250, 0.1283]]
这样一个矩阵,求一行中的最大值,即第二个维度dim=1上