机器学习入门--线性回归

参考网站：https://www.zybuluo.com/hanbingtao/note/448086

线性回归单元示图：

权重与偏置参数更新方法如下，其中看成偏置，其实是不存在的，可以认为，详细推演方法见参考网站，最终梯度为。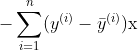

目标函数即误差函数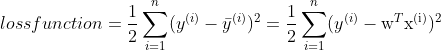，即为每个标签值与预测值差值平方和最小。误差函数越小，学习的效果越好。

参数更新采用梯度下降法：

实现代码：

思路其实和and(or)感知机中的算法实现思路相同

不同点如下：

1）输入这里是坐标值，不是0/1变量；

2）激活函数不同，感知机是阶跃函数，这里是线性函数；

同样，先定义线性函数需要的权重weight和偏置bias

#类 -- 集合中每个对象所共有的属性和方法
class Perceptron:
    def __init__(self):
        self.weight = 0.0
        self.bias = 0.0

主函数实现：

import os
import perceptron
from matplotlib import pyplot as plt
def activatorRelu(val):
    #线性激活函数
    return val

def updateWeight(label,weight,bias,rate,output,input):
    delta = label - output
    w1 = delta*input[0]*rate+weight
    bias = bias+rate*delta
    return w1,bias
 
def calcOutput(x1,w1,b):
    return x1*w1+b
 
if __name__=="__main__":
    #初始化，赋初值
    p1 = perceptron.Perceptron()
    print(p1.weight)
    print(p1.bias)
 
    #work time
    input = [[5],[3],[8],[1.4],[10.1]]
    #money
    label = [5500,2300,7600,1800,11400]
    learnRate = 0.1
    lun=0
    #训练迭代，更新权重、偏置
    while lun<=20:
        for x in input:
            print("lun:",lun,x)
            output = calcOutput(x[0],p1.weight,p1.bias)
            print("before activate output:",output)
            output = activatorRelu(output)
            print("after activate output:",output)
            # raise "\nend****"
            print("label:",label[input.index(x)],"index:",input.index(x))
            p1w,p1b = updateWeight(label[input.index(x)],p1.weight,p1.bias,learnRate,output,x)
            
            #更新学习率，若不更新，效果很差
            # if p1.weight-p1w < 1:
            #     learnRate = learnRate * 0.1
            p1.weight,p1.bias = p1w,p1b
            print(p1.weight,p1.bias)
            print("\n******************************************\n")
        lun = lun + 1
    
    #预测过程
    preInput = 10
    output = calcOutput(preInput,p1.weight,p1.bias)
    print("learnRate:",learnRate,"predict output:",output)
    output = activatorRelu(output)
    print("predict output:",output)
    
    #绘图显示
    x_axis=[]
    for x in input:
        x_axis.append(x[0]) 
    plt.scatter(x_axis,label,marker='x',color='green')
    plt.plot([0.1,12],[activatorRelu(calcOutput(0.1,p1.weight,p1.bias)),activatorRelu(calcOutput(12,p1.weight,p1.bias))])
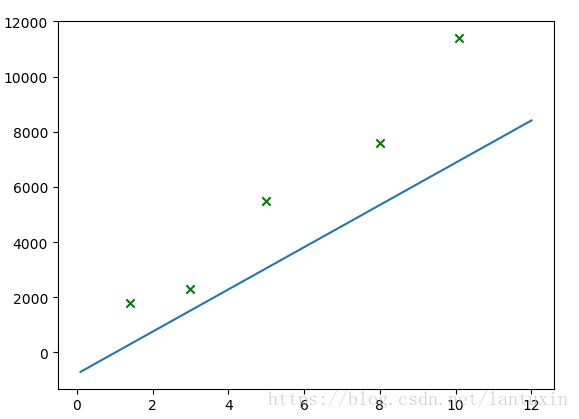
    plt.show()

学习率learnRate若一直保持0.1，最终线性回归图如下，难以达到理想的效果：

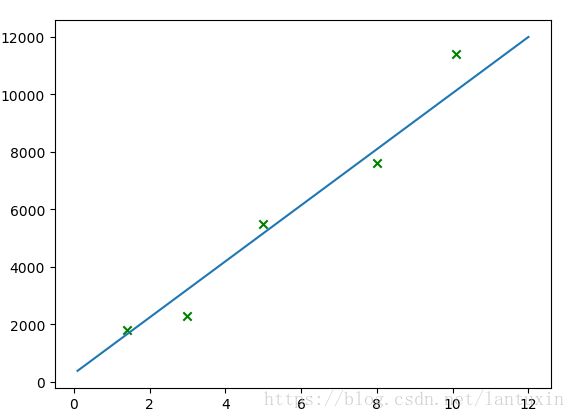
更新学习率learnRate（这里更新的方法可能欠考虑）之后，线性回归效果比较好：

可以想象，有几个变量（或者几维的变量），就可以用几个权重去逼近。