【视觉SLAM十四讲源码解读】坐标变换 Eigen、Sophus、旋转矩阵、轴角、旋转向量、欧拉角、四元数、位姿变换

实战教程

1_eigen_vector_matrix.cpp

2_eigen_math.cpp

3_eigen_pose_transform.cpp

4_plot_trajectory.cpp

5_trajectory_transform.cpp

6_sophus_pose_transform.cpp

7_trajectory_error.cpp

8_coordinateTransform.cpp

旋转矩阵(方向余弦)实现二维坐标变换

知两个轮子之间的距离，和两个轮子的速度，可以求出速度，角速度，半径。

旋转矩阵(方向余弦)实现三维坐标变换

车辆坐标系的原点在车辆后轮轴的中心

z轴 – 通过车顶垂直于地面指向上方

y轴 – 在行驶的方向上指向车辆前方

x轴 – 自车面向前方时，指向车辆右侧

无人车左前方的角雷达（Corner radar）安装位置和坐标系如下图

雷达检测到的障碍物如图中的绿点所示，绿点在雷达坐标系下的坐标为(x1,y1），为了便于理解暂不加入z方向的坐标。
绿点转换到车坐标系下需要经过一定的数学运算。基本思路是平移：先将角雷达坐标系的O点平移到与自车坐标系的O点重合，此时(x1,y1)需要减去两个坐标系在x和y方向的距离。如下图所示

旋转：在两个坐标系的O点重合后，将角雷达坐标系沿着z轴进行一定角度的旋转，这样(x1,y1)就转到了自车坐标系上。这个过程在数学上称为欧拉旋转。坐标系的平移和旋转是两件相互独立的事情，先平移再旋转和先旋转再平移并不会影响最终的结果。

平移：平移步骤根据传感器安装位置和自车后轴的距离进行计算，仅仅是XYZ三个方向加减运算。
旋转：绕轴旋转需要引入角度，不是简单的加减运算，所以我们通过图示来推导一下。
先将两个坐标系变换到正常的视角，如下图所示：

障碍物在雷达坐标系下的坐标为(x1,y1)，假设障碍物在自车坐标系下的坐标为(x0,y0)，需要根据安装角度α（可测量），用x1，y1，α这三个已知量表示x0，y0，求得他们的数学关系。

通过做辅助线进行计算，如下图蓝线所示所示：

几何关系可用以下两个等式表示：

使用矩阵表示，可以简化表达，用一个等式代替两个等式，是这样的

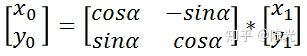
由于这次旋转是绕z轴旋转，因此旋转前和旋转后的z值是保持不变的

将z方向的值也放到上面的等式中，即可得到

那就意味着，只要把角雷达采集到的障碍物坐标值与上面这个矩阵进行矩阵乘法运算，即可完成沿Z轴的旋转。在这里我们把这个矩阵叫做Z轴旋转矩阵RZ，那必然还有沿着X轴和Y轴的旋转矩阵RX和RY。

角雷达目标的坐标依次右乘这三个矩阵，就完成了沿着Z轴，Y轴，X轴的旋转，得到的结果就是自车坐标系下的坐标值了。即

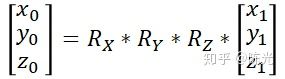
再加上一个平移的矩阵，就能够完整描述整个坐标转换的关系了

不同的坐标系定义，会有不同的RX，RY和RZ，因此需要根据实际情况计算旋转矩阵和平移矩阵。

欧拉角

欧拉角(Euler Angle)是可以表示3D空间中任何旋转的3个值
一共有3种欧拉角：俯仰角(Pitch)、偏航角(Yaw)和滚转角(Roll)

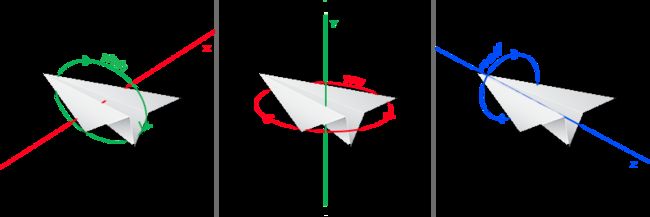
俯仰角是描述我们如何往上或往下看的角
偏航角表示我们往左和往右看的程度
滚转角代表我们如何翻滚摄像机，
每个欧拉角都有一个值来表示，把三个角结合起来我们就能够计算3D空间中任何的旋转向量了。

对于我们的摄像机系统来说，我们只关心俯仰角和偏航角，所以我们不会讨论滚转角。
给定一个俯仰角和偏航角，我们可以把它们转换为一个代表新的方向向量的3D向量。
俯仰角和偏航角转换为方向向量的处理需要一些三角学知识，我们先从最基本的情况开始：

如果我们把斜边边长定义为1，我们就能知道邻边的长度是cos x/h=cos x/1=cos x，它的对边是sin y/h=sin y/1=sin y。这样我们获得了能够得到x和y方向长度的通用公式，它们取决于所给的角度。我们使用它来计算方向向量的分量：

看看我们是否能够为偏航角找到需要的分量：

欧拉角描述刚体姿态的三个角，欧拉角有静态和动态两种，静态的是一直参考静止的惯性坐标系的三个轴进行旋转，而动态的在旋转过程中参考的旋转坐标轴会发生变化，除了第一次旋转是参考惯性系的坐标轴进行之外，后续两次旋转都是参考动态的，并且前面旋转的角度对后面的旋转轴是有影响的，按照不同的轴顺序进行旋转得到的欧拉角也是不同的，旋转变换可以归结为若干个沿着坐标轴旋转的组合，组合个数不超过三个并且两个相邻的旋转必须沿着不同坐标轴，总共有12种旋转方式，分别是XYZ、XZY、XYX、XZX、YXZ、YZX、YXY、YZY、ZXY、ZYX、ZXZ、ZYZ。ROS里面URDF采用的是XYZ(rpy)，规定右手坐标系中，物体旋转的正方向是右手螺旋方向。

先来介绍一下右手直角坐标系，在右手直角坐标系中,从原点看，沿每一根轴的顺时针方向定义为这根轴的正向转动,负向转动正好相反,即为
逆时针方向。

当参考不同的轴系作一系列转动时，载体姿态的变化不仅是绕每根轴转动角度的函数，而且还是转动顺序的函数，也就是轴和方向都有影响。

左半图转动的顺序是：先绕俯仰轴 y 转动 90，再绕偏航轴 z 转动 90，最后绕俯仰轴 y 转动 90
依次完成转动后可以看到绕横滚轴 x 发生了 90 的净转动。

右半图中转动的顺序正好相反，虽然转动结束时，载体的横滚轴仍对准在原来的方向，但横滚轴 x 发生了 -90 的净转动。
各个轴的转动顺序是不可交换的，很明显如不考虑轴系的转动顺序，在计算姿态时将会引起很大的误差。

欧拉角和旋转矩阵

旋转矩阵与四元数

旋转矩阵与旋转矢量

四元数与旋转向量

假设某个旋转运动的旋转轴为单位向量 u，绕该轴旋转的角度为 θ,那么它对应的单位四元数为:

// euler2Rotation:  // body frame to world frame ? body frame to interitail frame
Eigen::Matrix3d euler2Rotation( Eigen::Vector3d  eulerAngles){
    double roll = eulerAngles(0);
    double pitch = eulerAngles(1);
    double yaw = eulerAngles(2);

    double cr = cos(roll);
    double sr = sin(roll);
    double cp = cos(pitch);
    double sp = sin(pitch);
    double cy = cos(yaw);
    double sy = sin(yaw);

    Eigen::Matrix3d RIb;
    RIb<< cy*cp ,   cy*sp*sr - sy*cr,   sy*sr + cy* cr*sp,
            sy*cp,    cy *cr + sy*sr*sp,  sp*sy*cr - cy*sr,
            -sp,         cp*sr,           cp*cr;

    Eigen::AngleAxisd rollAngle(Eigen::AngleAxisd(eulerAngles(0),Eigen::Vector3d::UnitX()));
    Eigen::AngleAxisd pitchAngle(Eigen::AngleAxisd(eulerAngles(1),Eigen::Vector3d::UnitY()));
    Eigen::AngleAxisd yawAngle(Eigen::AngleAxisd(eulerAngles(2),Eigen::Vector3d::UnitZ()));

    Eigen::Matrix3d rotation_matrix;
    rotation_matrix=yawAngle*pitchAngle*rollAngle;
    std::cout << "rotation_matrix " << rotation_matrix <<  std::endl;

    std::cout << "RIb " << RIb <<  std::endl;

    return RIb;
}

Eigen::Matrix3d eulerRates2bodyRates(Eigen::Vector3d eulerAngles){
    double roll = eulerAngles(0);
    double pitch = eulerAngles(1);

    double cr = cos(roll);
    double sr = sin(roll);
    double cp = cos(pitch);
    double sp = sin(pitch);

    Eigen::Matrix3d R;
    R<<     1,   0,    -sp,
            0,   cr,   sr*cp,
            0,   -sr,  cr*cp;
    return R;
}

Eigen、Sophus位姿变换

1. 旋转矩阵也叫方向余弦表示刚体的姿态
   方向余弦矩阵是一个 3 x3 阶的矩阵,矩阵的列表示载体坐标系中的单位矢量在参考坐标系中的投影。

2. 轴角也叫旋转向量表示刚体的姿态
   任意旋转都可以用一个旋转轴和一个旋转角刻画,旋转向量可以由罗德里格斯公式转换成旋转矩阵

3. 欧拉角表示刚体的姿态
   从一个坐标系到另一个坐标系的变换可以通过依次绕不同坐标轴的3次连续转动来定义。
   从物理角度看,欧拉角表示法可能是最简单的方法之一。

4. 四元数表示刚体的姿态
   四元数姿态表示法,通过绕参考坐标系中二个矢量的单次转动来实现，一个坐标系到另一个坐标系的转换。
   四元数是一个具有四个元素的矢量表达式,各个元素为矢量方向和转动大小的函数。

Eigen中的欧拉角转成ROS::tf中的四元数

ROS中这个函数是绕动轴转动：tf::createQuaternionMsgFromRollPitchYaw(roll_x, pitch_y, yaw_z)

Eigen中欧拉角转动顺序是采用绕动轴转动的变换方式

特殊正交群$SO(n)$->旋转矩阵群$SO(3)$->李群$SO(3)$旋转矩阵
特殊欧氏群$SE(n)$->变换群$SE(3)$->李群$SE(3)$变换矩阵

李群是指具有连续（光滑）性质的群。像整数群 Z 那样离散的群没有连续性质，所以不是李群。
而$SO(n)$和$SE(n)$，它们在实数空间上是连续的，能够直观地想象一个刚体能够连续地在空间中运动。

李代so(3) 三维向量实际上是旋转向量组成的空间
李代se(3) 六维向量 平移在前 旋转在后

旋转矩阵的导数由旋转向量指定，指导着如何在旋转矩阵中进行微积分运算。
每个李群都有与之对应的李代数，李代数描述了李群的局部性质。
李代数描述了李群的局部性质，准确地说是单位元附近的正切空间。
李群$SO(3)$的李代数so(3)是一个由三维旋转向量组成的空间，每个向量对应一个反对称矩阵，可以用于表达旋转矩阵的导数李代数$SO(3)$的关系由指数映射即罗德里格斯公式给定。

定义对数映射可以把李群中的元素对应到李代数旋转矩阵的导数就是旋转向量，指导者如何在矩阵中进行微积分运算，李代数的一大动机是为了进行优化。

Eigen是C++线性代数库，提供矩阵的线性代数运算，包括解方程，但没有提供李代数的支持。
Sophus是李群和李代数库，它支持李群SO3 李代so3 李群SE3 李代se3。
Sophus库是基于Eigen基础上开发的，继承了Eigen库中的定义的各个类。
因此在使用Eigen库中的类时，既可以使用Eigen命名空间，也可以使用Sophus命名空间。

高博这张图总结的很好

欧式变换　$SE(3)$

相似变换　$sim(3)$

摄影变换　小孔成像

Eigen::SelfAdjointEigenSolver＜Eigen::MatrixXd＞

http://eigen.tuxfamily.org/dox-3.2/classEigen_1_1SelfAdjointEigenSolver.html

在数学里，作用于一个有限维的内积空间，一个自伴算子（self-adjoint operator）等于自己的伴随算子；等价地说，在一组单位酉正交基下，表达自伴算子的矩阵是埃尔米特矩阵。埃尔米特矩阵等于自己的共轭转置。根据有限维的谱定理，必定存在着一个正交归一基，可以表达自伴算子为一个实值的对角矩阵。

矩阵A的共轭转置（英语：conjugate transpose，又称埃尔米特共轭、埃尔米特转置（英语：Hermitian transpose））

内积空间是数学中的线性代数里的基本概念，是增添了一个额外的结构的向量空间。这个额外的结构叫做内积或标量积。内积将一对向量与一个标量连接起来，允许我们严格地谈论向量的“夹角”和“长度”，并进一步谈论向量的正交性。内积空间由欧几里得空间抽象而来（内积是点积的抽象），这是泛函分析讨论的课题。

内积空间有时也叫做准希尔伯特空间（pre-Hilbert space），因为由内积定义的距离完备化之后就会得到一个希尔伯特空间。

在早期的著作中，内积空间被称作酉空间，但这个词现在已经被淘汰了。在将内积空间称为酉空间的著作中，“内积空间”常指任意维（可数或不可数）的欧几里德空间。

数学上，特别是泛函分析中，希尔伯特空间中的每个线性算子有一个相应的伴随算子（adjoint operator）。算子的伴随将方块矩阵共轭转置推广到（可能）无穷维情形。如果我们将希尔伯特空间上的算子视为“广义复数”，则一个算子的伴随起着一个复数的共轭的作用。

在线性代数中，一个方形矩阵的伴随矩阵（英语：adjugate matrix）是一个类似于逆矩阵的概念。如果矩阵可逆，那么它的逆矩阵和它的伴随矩阵之间只差一个系数。然而，伴随矩阵对不可逆的矩阵也有定义，并且不需要用到除法。

伴随变换体现在矩阵上就是转置。

MP91：对偶空间、内积与辛结构
MP92：复共轭转置与伴随算子

坐标变换 坐标系之间坐标点的变换

首先要理解如下概念

向量也就是坐标系下面的坐标点，在世界坐标系w下的坐标是$p_w$，在机器人坐标系r下的坐标是$p_r$

下面公式就可以将机器人坐标系下的坐标点转换到世界坐标系下面。

$p_w$ = $R_{wr}$$p_r$ + $t_{wr}$

$R_{wr}$：把坐标系r的向量也就是坐标系下面的坐标点变换到坐标系w中

$T_{wr}$：把机器人坐标系下的向量也就是坐标系下面的坐标点变换成世界坐标系下的坐标

$O_r$：机器人坐标系的原点
$O_w$：机器人坐标系的原点在世界坐标系下面的坐标
$O_w$ = $t_{wr}$ = $T_{wr}$$O_r$

$t_{wr}$：机器人坐标系原点在世界坐标系下的坐标点

接下来看题目
已知：
１号萝卜坐标系下面的坐标点：
$r_1$坐标系下面的点的坐标$p_{r1}$ = $[0.5,-0.1,0.2{]}^T$
已知：
从世界坐标系到相机（萝卜）坐标系的变换关系
$r_1$的位姿为：$q_1$ = [0.55, 0.3, 0.2, 0.2]， $t_1$ =$[0.7,1.1,0.2{]}^T$
$r_2$的位姿为： $q_2$ = [−0.1, 0.3, −0.7, 0.2]， $t_2$ = $[-0.1,0.4,0.8{]}^T$
$r_1$的位姿可以把世界坐标系下面的坐标点变换到机器人$r_1$坐标系下表示为$T_{r1w}$
$r_2$的位姿可以把世界坐标系下面的坐标点变换到机器人$r_2$坐标系下表示为$T_{r2w}$
求：
$r_2$坐标系下面的点的坐标$p_{r1}$ = $[x,y,z{]}^T$
求解思路：
就是先把１号萝卜坐标系下的坐标点$p_{r1}$变换到世界坐标系下面$T_{r1w}$.inverse() * $p_{r1}$，然后再变换到２号萝卜坐标系$r_2$下$T_{r2w}$
公式如下：
$p_{r2}$ = $T_{r2w}$ * $T_{r1w}$.inverse() * $p_{r1}$

ORB_SALM2的坐标变换

/**
 * 设置当前帧相机光/中心也就是当前相机坐标系在相机第一帧世界坐标系下的3D点坐标
 */
inline cv::Mat GetCameraCenter(){return mOw.clone();}

/**
 * mRwc存储的是从当前相机帧坐标系到相机第一帧世界坐标系的旋转设置为相机当前帧的姿态
 * 一般的旋转是从相机第一帧世界坐标系到当前相机帧的坐标系的旋转所以要求旋转矩阵的逆
 */
inline cv::Mat GetRotationInverse(){
    return mRwc.clone();
}

// 将相机第一帧世界坐标系变换到相机当前帧坐标系的变换矩阵设置为当前相机帧的位置姿态
void SetPose(cv::Mat Tcw){
    mTcw = Tcw.clone();
    UpdatePoseMatrices();
}

/**
 * Computes rotation, translation and camera center matrices from the camera pose.
 * 根据相机当前帧位姿Tcw,计算相机当前帧的旋转矩阵mRcw,旋转矩阵的逆mRwc,平移向量mtcw和相机光/中心mOw
 */
void UpdatePoseMatrices(){
    // cv::Mat mTcw; 相机第一帧世界坐标系到相机当前帧坐标系的变换矩阵，也就是相机当前帧的位姿（借助两张图像求解Rt可以理解为相机前一时刻到当前时刻做了多少旋转，做了多少平移，如果是正数代表向正方向移动，如果是正的旋转代表旋转方向是从x的正方向向y的正方向旋转，符合笛卡尔坐标系规则，注意这里要要和相机图像坐标系做区分，因为图像的坐标系原点在左上角，ｘ向右，ｙ向下，而笛卡尔坐标系ｘ向右，ｙ向上，原点在左下角，还有就是右手系规则）
 
    mRcw = mTcw.rowRange(0,3).colRange(0,3);

    // cv::Mat mRcw; 相机第一帧世界坐标系到相机当前帧坐标系的旋转矩阵
    // cv::Mat mRwc; 相机当前帧坐标系到相机第一帧的旋转矩阵
    // mRwc = mRcw求逆
    mRwc = mRcw.t();

    // cv::Mat mtwc; 相机当前帧坐标系到相机第一帧世界坐标系的平移向量
    // cv::Mat mtcw; 相机第一帧世界坐标系到相机当前帧坐标系的平移向量
    mtcw = mTcw.rowRange(0,3).col(3);
    
    // cv::Mat mOw; 相机当前帧光心在相机第一帧世界坐标系下的坐标
    mOw = -mRcw.t()*mtcw;
}

const float z = mvDepth[i];
const float u = mvKeysUn[i].pt.x;
const float v = mvKeysUn[i].pt.y;
const float x = (u-cx)*z*invfx;
const float y = (v-cy)*z*invfy;
// 生相机当前帧坐标系下的3D空间点
cv::Mat x3Dc = (cv::Mat_<float>(3,1) << x, y, z);
// 相机当前帧坐标系下的2D像素点生成3D空间点，然后左乘mRwc*x3Dc加上平移mOw生成相机第一帧世界坐标系下面的3D空间点。
return mRwc*x3Dc+ mOw;

小萝卜坐标变换代码实战

#include 
#include 
#include 

int main() {
    // 构造世界坐标系到R1坐标系的变换矩阵
    Eigen::Quaterniond q1(0.35, 0.2, 0.3, 0.1); // 四元数表示的旋转矩阵
    std::cout << "q1 = " << std::endl << q1.x() << std::endl << q1.y() << std::endl << q1.z() << std::endl << q1.w() << std::endl;
    /*
    * q1 =
    * 0.2
    * 0.3
    * 0.1
    * 0.35
    */
    q1.normalize(); // 可以看到归一化后数字的精度和大小都会发生变化
    std::cout << "q1 = " << std::endl << q1.x() << std::endl << q1.y() << std::endl << q1.z() << std::endl << q1.w() << std::endl;
    /*
     * q1 =
     * 0.39036
     * 0.58554
     * 0.19518
     * 0.68313
     */
    // 位姿的四元数表示和平移向量转化为欧式变换矩阵
    Eigen::Isometry3d T1w(q1);
    Eigen::Vector3d t1(0.3, 0.1, 0.1); // 平移向量
    T1w.pretranslate(t1);
    // 输出位姿矩阵信息
    std::cout << "T1w: " << std::endl << T1w.matrix() << std::endl;
    /*
     * T1w:
     *  0.238095   0.190476   0.952381        0.3
     *  0.72381    0.619048  -0.304762        0.1
     * -0.647619   0.761905   0.00952381      0.1
     *  0          0          0               1
     */
    // R1坐标系下点p1的坐标
    Eigen::Vector3d p1(0.5, 0, 0.2);

    // 构造世界坐标系转到R2坐标系的变换矩阵
    Eigen::Quaterniond q2(-0.5, 0.4, -0.1, 0.2); // 四元数表示位姿 旋转矩阵
    q2.normalize(); // 归一化
    Eigen::Isometry3d T2w(q2);
    Eigen::Vector3d t2(-0.1, 0.5, 0.3); // 平移向量
    T2w.pretranslate(t2);
    std::cout << "T2w: " << std::endl << T2w.matrix() << std::endl;
    
    // T1w.inverse() * p1 ->把R1坐标系的坐标点p1变换到世界坐标系下
    // T2w * T1w.inverse() * p1 ->世界坐标系下的坐标点p1变换到R2坐标系下
    Eigen::Vector3d p2 = T2w * T1w.inverse() * p1;

    std::cout << std::endl << "p1: " << p1.transpose() << std::endl;
    std::cout << std::endl << "p2: " << p2.transpose() << std::endl;
    return 0;
}

编译文件

CMakeLists.txt

cmake_minimum_required(VERSION 2.8)

project(chapter3)

set(CMAKE_CXX_FLAGS "-std=c++11")

set(EIGEN3_INCLUDE_DIRS /usr/local/include/eigen3)
include_directories(${EIGEN3_INCLUDE_DIRS})

add_executable(coordinateTransform coordinateTransform.cpp)

编译步骤

把源文件和编译文件放在同一个路径下面进行编译
如何编译可以参考这篇文章视觉SLAM十四讲实践笔记教程

mkdir build
cd build
cmake ..
make -j4

运行程序

./coordinateTransform