【ORB-SLAM2源码解读】论文公式

ORB_SLAM2论文翻译

ORB-SLAM2 论文全文翻译

robust Huber cost function

在统计学习角度，Huber损失函数是一种使用鲁棒性回归的损失函数，它相比均方误差来说，它对异常值不敏感。常常被用于分类问题上。

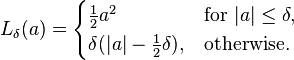
这个函数对于小的a值误差函数是二次的，而对大的值误差函数是线性的。变量a表述residuals，用以描述观察值与预测值之差：a = y - f(x)，因此我们可以将上面的表达式写成下面的形式：

协方差矩阵

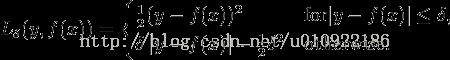
如何直观地理解「协方差矩阵」？

数学求和符号用法大汇总

1、代数领域
（1）数集
N自然数集：Natural number（英语）
R实数集：Real number（英语）
Q有理数集：Quotient（德语）商的意思【因为所有的有理数都可以表示成整数的比的形式】
Z整数集：Zahlen（德语）

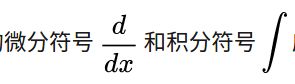
马同学
最小二乘法的本质是什么？
https://www.zhihu.com/question/37031188/answer/138751254

5 个在数学符号方面寻求帮助的小建议

本部分将列示一些当你被机器学习中的数学符号折磨时可以用到的小建议。

考虑一下作者

你在阅读的论文或者书籍总有一个作者。这个作者可能犯错，可能有疏忽，也可能是因为他们自己也不明白自己在写什么，才让你如此迷惑。从符号的限制中逃离片刻，然后想想作者的目的。他们到底想把什么讲清楚？也许你甚至可以用电子邮件、Twitter、Facebook、领英等方式来联系作者让他帮你解释清楚。你放心，大多数学者都希望其他人能够理解并好好利用他们的研究成果。

上维基百科查一查

维基百科上有符号列表，可以帮助你缩小符号含义的可能范围。我建议你从这两个词条开始：

「数学符号表」（https://en.wikipedia.org/wiki/List_of_mathematical_symbols）「数学、科学和工程中的希腊字母」（https://en.wikipedia.org/wiki/Greek_letters_used_in_mathematics,_science,_and_engineering）

用代码简述出来

数学运算不过就是对数据进行函数处理。把你读到的任何东西都用变量、for-循环等写成伪代码展示出来。这个过程中你可能打算使用某个脚本语言来处理自己随意写出来的数组，或者甚至一张 Excel 表格的数据。

当你阅读并理解了文章中的技术改进，那你随之写出来的核心代码才会取得更好的结果，最终经过不断的改进，你就会写出一个小小的原型机，可以自己玩耍了！我一度不相信这个方法行得通，直到看到一个学者仅用几行 MATLAB 代码和随意编写的数据就写出了一篇非常复杂的论文的核心代码。这令我大吃一惊，因为我以前一直坚信机器学习的系统必须完整地编写出来并且使用真实数据才能运行，所以要学习任何一篇文章只有找到原始的代码和数据这一条路可走。但是我真的错了。不过话说回来，那个学者真的是个天才。

现在我一直都在用这种方法学习机器学习，不过我是用 Python 写出新学到的技巧的核心代码。

换条路试试

有一个我在搞懂新技术时常用的小技巧，即找到所有引用了包含该技术的论文的其他论文，看看其他人如何演绎、解释这个新技术时常能够解除我在读原始描述产生的误解。不过这个办法不总是有效，反而会更加迷惑，引入了更多令人误解的方法和新符号。但是总体来说，这个办法还是有效的。

在网上向大神请教

说实话，有很多线上论坛里的人们很愿意向别人解释数学。你可以在屏幕上截张困扰你的符号图，写清楚出处和链接，然后连同你的困惑一起发布在问答网站上。推荐以下两个入门网站：

https://math.stackexchange.com/https://stats.stackexchange.com/

Spanning Graph Covisibility Graph Essential Graph

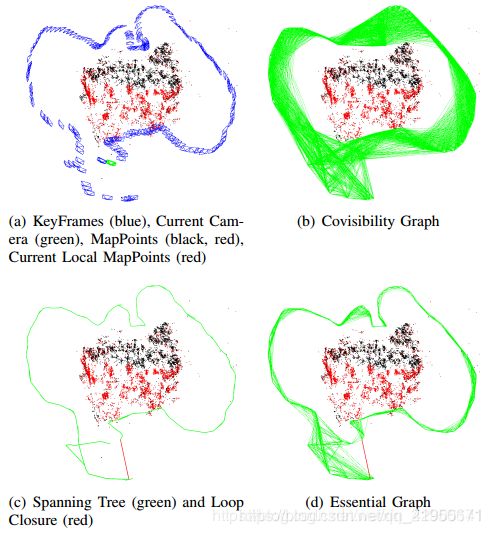
在Orb-Slam中有三个地图分别是Covisibility Graph，Spanning Graph，以及Essential Graph，它们三个分别是什么意思呢？

首先，图优化是目前视觉SLAM里主流的优化方式。其思想是把一个优化问题表达成图（Graph），以便我们理解、观察。如果题主想更清楚地认识图优化与SLAM的关系

一个图中有很多顶点，以及连接各顶点的边。当它们表示一个优化问题时，顶点是待优化的变量，而边是指误差项。我们把各个边的误差加到一起，就得到了整个优化问题的误差函数。

顶点的参数化形式可以有很多不同的样子。例如某些顶点可以表示相机的Pose，另一些顶点可以表示三维空间点。同理，边也有不同的形式。除了个别的顶点和边，我们也关心整个图的结构，例如连通性等。

图中红色点可看成关键帧相机Pose，青色点表示空间点，蓝色和红色边表示Pose-Pose的边，而黄色边表示Pose-Point的边。
Spanning graph理解成生成树更好一些。

如果我们考虑所有的相机 Pose 和所有点的空间位置，构造出的图将会非常复杂，而难以直接进行实时优化。因此，通常我们会构建一些带有特殊结构的图，以满足实时性的需要。

最简单的是Pose Graph。如果我们对特征点的空间位置并不关心，就可以构建只带有Pose结点，以及Pose-Pose边这样的图。由于一个照片中常常有上千个特征点，这样做可以节省许多计算量。
Covisilibilty Graph 的顶点是相机的Pose，而边是Pose-Pose的变换关系——所以也算是Pose Graph 一种吧。当两个相机看到相似的空间点时，它们对应的Pose就会产生联系（我们就可以根据这些空间点在照片上的投影计算两个相机间的运动）。根据观测到的空间点的数量，给这个边加上一个权值，度量这个边的可信程度。

Covisibility Graph是一个无向有权图(graph),这个概念最早来自2010的文章[Closing Loops Without Places]。简单来说，每个node就是关键帧，edge的权重就是两个关键帧找到足够多的相同的 3d 点的数目。

Essential Graph 比Covisibility Graph更为简单，ORB-SLAM主要用它来进行全局优化。为了限制优化的规模，ORB-SLAM试图尽量减少优化边的数量。而尽量减少边，又保持连通性的方法，就是做一个最小生成树。

为了在优化阶段减小计算量，作者提出了Essential Graph的概念，这个能够连接所有的node，但是edge会减少很多。可以认为是Covisibity Graph的最小生成树（MST）。

Covisibility 是一直在用的概念，而Essential Graph是orbslam自己提出的概念，为了减小全局回环的计算量。当你自己实现SLAM时，也会碰到这些困难，并设计一些应对的策略，这些就是你的创新性。事实上，随着SLAM时间的增长，如何控制图的结构和优化的规模，仍是现在SLAM有待解决的一个问题。

我的理解：

1.covisibility graph
顶点：相机的 pose
边：pose 和 pose 间的位置关系
权值：边的可信度（每条边都有自己的权值）

具体到orb_slam2上，其表示了，每个关键帧处的相机位置之间的关系“图”

2.essential graph
顶点：相机的 pose
边：pose 和 pose 间的位置关系
权值：边的可信度（每条边都有自己的权值）

是orb_slam2中主要用的“图”。
是对 covisibility graph 的优化（边最少、置信值高、保持连通性）

我们提出构建一个（Essential Graph），该图中保留了covisibility graph的所有节点（关键帧），但是边缘更少，仍旧保持一个强大的网络以获得精确的结果。系统从初始关键帧开始增量式地构建一个生成树，它是一个边缘数量最少的covisibility graph的子图像。当插入新的关键帧时，则判断其与树上的关键帧能共同观测到多少云点，然后将其与共同观测点最多的关键帧相连反之，当一个关键帧通过筛选策略被删除时，系统会重新更新与其相关的连接。Essential Graph包含了一个生成树，一个高covisibility（θmin=100）的covisibility graph边缘子集，以及闭环回路的边缘，这样的组合共同构建了一个强大的相机网络。图2展示了一个covisibility graph，生成树和相关的essential graph的例子。在本文第8部分第E节的实验里，当算法运行位姿图优化时，结果可以达到非常高的精度以至于即便是全局BA优化都很难达到。。essential graph的效用和θmin对算法的影响将在第8部分E节的最后讨论。

非线性优化