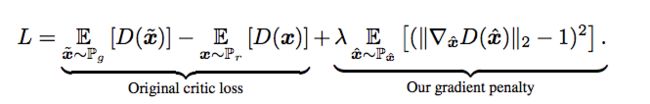【读点论文】ViTGAN: Training GANs with Vision Transformers 将视觉transformer和gan结合起来

ViTGAN: Training GANs with Vision Transformers

Abstract

• 最近，Vision Transformers(vits)在图像识别方面表现出了具有竞争力的性能，需要较少的视觉特定的归纳偏差。

• 在本文中，研究这种观察是否可以扩展到图像生成。将ViT整合到生成式对抗网络(GANs)中。本文观察到，现有的GANs正则化方法与自注意力的交互作用很差，导致训练过程中严重的不稳定性。

• 为了解决这个问题，引入了新的正则化技术来训练具有vit的gan。根据经验，本文的方法ViTGAN在CIFAR-10、CelebA和LSUN bedroom数据集上取得了与基于CNN的StyleGAN2相当的性能。以确保其训练稳定性和提高收敛性。

• 引入了新的正则化技术来训练带有ViT的GAN，得出以下研究结果：

  • ViTGAN模型远优于基于Transformer的GAN模型，在不使用卷积或池化的情况下，性能与基于CNN的GAN（如Style-GAN2）相当(还差点)。
  • ViTGAN模型是首个在GAN中利用视觉Transformer的模型。
  • ViTGAN模型展示了在标准图像生成基准（包括CIFAR、CelebA和LSUN bedroom数据集）中，这种Transformer与最先进的卷积架构具有可比性的方法。

Introduction

• 卷积神经网络(CNN)目前正主导着计算机视觉，这要归功于它们强大的卷积(权重共享和局部连接)和池化(translation equivariance)能力。然而，transformer架构已经开始在图像[Generative pretraining from pixels，ViTs，Training data-efficient image transformers & distillation through attention]和视频[Is space-time attention all you need for video understanding?，Vivit: A video vision transformer]识别任务中与CNN竞争。

• 特别是视觉变形器(ViTs) ，它将图像解释为一系列符号(类似于自然语言中的单词)，Dosovitskiy等人已经在ImageNet基准测试中展示了以更小的计算预算(即更少的FLOPs)实现可比的分类精度。与CNN中的局部连接不同，vit依赖于全局上下文化的表示，其中每个patch都关注同一图像的所有patch。

• vit及其变体[Mlp-mixer]虽然仍处于起步阶段，但已经在建模非本地上下文依赖以及卓越的效率和可扩展性方面显示出了有希望的优势。自最近问世以来，ViTs已被用于各种其他任务，如对象检测，视频识别，多任务预训练等。

• 在本文中感兴趣的是检验图像生成的任务是否可以在不使用卷积或池的情况下通过视觉transformers来实现，更具体地说，是否可以使用ViTs来训练生成性对抗网络(gan),使其具有与基于CNN的gan竞争的质量。

• 为此，按照原始ViT的设计，用Vanilla-ViT(如下图 (A))训练GANs。挑战在于，当与vit结合时，GAN训练变得非常不稳定，并且在鉴别器训练的后期阶段，对抗性训练经常受到高方差梯度(或尖峰梯度)的阻碍。

  • • 偏差： 描述的是预测值（估计值）的期望与真实值之间的差距。偏差越大，越偏离真实数据集。

    • 方差： 描述的是预测值的变化范围，离散程度，也就是离其期望值的距离。方差越大，预测结果数据的分布越散。

    • 如果训练集设置非常好，而验证集设置相对较差，可能过度拟合了训练集，某种程度上，验证集并没有充分利用交叉验证集的作用。这种情况就是高方差（high variance）。

    • 算法并没有在训练集中得到很好的训练，如果训练数据的拟合度不高，就是欠拟合，可以说这种算法偏差比较高（high bias）

      • 

    • 解决高方差

      • 更多的数据
      • 正则化（regularization）：利用正则化来解决high variance的问题，正则化是在cost function中加入一项正则化项，惩罚模型的复杂度
      • 寻找合适的网络结构

    • 为什么加入正则化会减小过拟合即为什么减小方差？

      • 以逻辑回归为例加入正则项的代价函数$J(w,b)=\frac{1}{m}{\sum }_{i=1}^{m}l({\hat{y}}^{(i)},y^{(i)})+\frac{\lambda }{2m}||w|{|}_2^2$。
      • 加入的时L2正则项。其中λ为正则因子。当正则因子λ设置的足够大的情况下，为了使代价函数最小化，权重矩阵W就会被设置为接近于零的值，这就相当于消除了很多神经元的影响，那么网络就变得小了。但是实际上隐藏层的神经元依然存在，它们的影响变小了，就不会导致过拟合了。

  • 

• 此外，传统的正则化方法，如梯度惩罚，频谱归一化不能解决不稳定性问题，即使它们被证明是有效的基于CNN的GAN模型。由于不稳定训练在基于CNN的GANs训练中并不常见，且经过适当调整，这对基于ViT的GANs的设计提出了独特的挑战。

  • 梯度惩罚(一种正则惩罚函数)

    • LSGAN采用了一种 Least Squares loss的计算方式来加大gradient的有效传递， 而WGAN也给出了一种新的 Wasserstein distance 来解决梯度和崩溃的问题。 这次要提到的 WGAN-gp 是WGAN的一种改良版本，全称是 WGAN with gradient penalty。（引用于莫烦python https://mofanpy.com/）

    • WGAN的提出是GAN技术上的一个重大提高，它部分解决GAN训练不稳定的问题，不再需要小心平衡生成器和判别器的训练程度，基本解决了collapse mode的问题，确保了生成样本的多样性，并且在训练过程中终于有一个像交叉熵、准确率这样的数值来指示训练的进程，这个数值越小代表GAN训练得越好，代表生成器产生的图像质量越高。

    • 下面的右边（b）这张图，很多颜色线条那个是随着判别器层数增加， Clip 方案中梯度传导是有问题的，要么爆炸要么消失了，而 Gradient penalty 方案可以让每一层的梯度都比较稳定。

      • 
      • 惩罚的区域也如上图右中的蓝色区域，只有这部分的距离才会影响 $P_{data}$ 和$P_G$的近似。此时的Wasserstein距离就定义为：
        • 

    • Clip 方案网络中 weights 参数都跑到的极端的地方，要么最大，要么最小，而 Gradient penalty 方案可以让 weights 比较均匀地分布。

    • 

      • 公式里面表达的是它在WGAN的loss上加了一个惩罚项，如果判别器的 gradient 的 norm，离 1 越远，那么 loss 的惩罚力度越高。
      • 一般的GAN，通常会在判别器上加一些 batchNorm，但对于WGAN-gp的判别器，是不能加 batchNorm 的，原因很简单， 是因为WGAN-gp的惩罚项计算中，惩罚的是单个数据的gradient norm，如果使用 batchNorm，就会扰乱这种惩罚，让这种特别的惩罚失效。

    • 在每一次训练生成器时，要多训练几次判别器， 判别器首先需要采样一次正式数据和生成数据，然后拿着生成数据和真实数据去计算 gradient penalty. 计算 gradient penalty 的时候有几个步骤。

      • 拿到生成数据
      • 将生成数据和真实数据按一个比例混合（在照片数据值上的混合）
      • 用这个数据输入判别器，拿到输入判别器图片数据的梯度，注意这里并不是判别器网络weights的梯度
      • 对梯度计算 norm，看看这个 norm 离单位距离 1 有多远（离1越近，惩罚越小）

    • 要求 ‖T‖L ≤ 1 是在每一处都成立，所以数据应该是全空间的均匀分布才行， 显然这很难做到。所以作者采用了一个非常机智的做法： 在真假样本之间随机插值来惩罚，这样保证真假样本之间的过渡区域满足 1-Lipschitz 约束。

      • 

    • 1-Lipschitz函数

      • 是在一个连续函数 f上额外施加了一个限制，要求存在一个常数K≥0，使得定义域内的任意两个元素 x1,x2 都满足 $|f(x_1)-f(x_2)|\le K|x_1-x_2|$,称函数 f 的Lipschitz常数为K。当K=1时，称为“1-Lipschitz”。
      • 比如说连续函数f的定义域是实数集合，那上面的要求就等价于f的导函数绝对值不超过K。即，Lipschitz连续条件限制了一个连续函数的最大局部变动幅度。

  • 频谱归一化

    • WGAN虽然性能优越，但是留下一个难以解决的1-Lipschitz问题，SNGAN便是解决该问题的一个优秀方案。

    • Lipshcitz限制

      • 在最简单的一元函数中的形式即:$|f(x_1)-f(x_2)|\le k|x_1-x_2|$。要求f(x)任意两点之间连线的“斜率”绝对值小于Lipshcitz常数k。在WGAN中要求k=1，1-Lipshcitz限制要求保证了输入的微小变化不会导致输出产生较大变化。
      • 引入利普希茨连续性约束，使神经网络对输入扰动具有较好的非敏感性，从而使训练过程更稳定，更容易收敛。比如：深度学习模型存在“对抗攻击样本”，比如图片只改变一个像素就给出完全不一样的分类结果，这就是模型对输入过于敏感的案例。
      • Spectral normalization for generative adversarial network” 使用一种更柔和的方式使得判别器 D 满足利普希茨连续性，限制了函数变化的剧烈程度，从而使模型更稳定。

    • 原生 GAN 的目标函数等价于优化生成数据的分布 $P_g$ 和真实数据的分布 $P_r$ 之间的 J-S 散度 (Jensen–Shannon Divergence。在但存在的问题是判别器训练越好，生成器梯度消失越严重。

    • 关于生成器梯度消失的论证：在（近似）最优判别器下，最小化生成器的loss等价于最小化 $P_r$ 与之 $P_g$ 间的JS散度，而由于 $P_r$ 与之 $P_g$ 几乎不可能有不可忽略的重叠，所以无论它们相距多远JS散度都是常数$log2$，最终导致生成器的梯度（近似)为0，梯度消失。

    • Spectral Normalization的做法就很简单： 将神经网络的每一层的参数W 作 SVD 分解，然后将其最大的奇异值限定为1，满足1-Lipschitz条件， 具体地，在每一次更新 W 之后都除以 W 最大的奇异值。 这样，每一层对输入x 最大的拉伸系数不会超过 1。

    • 经过 Spectral Norm 之后，神经网络的每一层 $g_l(x)$ 权重，都满足

      • $$\frac{g_l(x)-g_l(y)}{x-y}\le 1$$

      • 对于整个神经网络 $f(x)=g_N(g_{N-1}(...g_1(x)...))$ 自然也就满足利普希茨连续性了。原因如下：

      • • 一致性||AB||<=||A|| ||B||
        • 线性性：对于任意系数α有，||αA||=|α| ||A||

    • 对多层神经网络，是多个复合函数嵌套的操作。最常见的嵌套是：一层卷积，一层激活函数，再一层卷积，再一层激活函数，这样层层包裹起来。而激活函数通常选取的 ReLU，Leaky ReLU 都是 1-Lipschitz 的，只需要保证卷积的部分是 1-Lipschitz continuous 的，就可以保证整个神经网络都是 1-Lipschitz continuous 的。

    • 而在图像上每个位置的卷积操作，正好可以看成是一个矩阵乘法。因此，我们只需要约束各层卷积核的参数 W ，使它是 1-Lipschitz continuous 的，就可以满足整个神经网络的 1-Lipschitz continuity。而已经知道，想让矩阵满足 1-Lipschitz continuous，只需要让它所有元素同时除以它的最大奇异值，或者说是它的 spectural norm。

    • 最大特征值（奇异值）(引用于言有三)

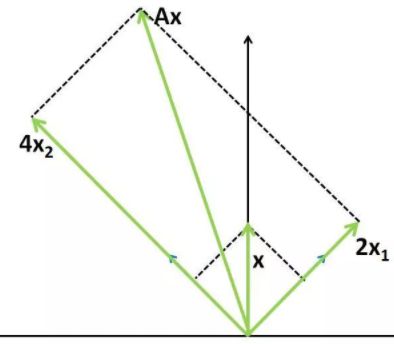
      • 从矩阵的特征值、奇异值开始说起。在线性代数中，Ax=b表示对向量x做矩阵A对应的线性变换，可以得到变换后的向量b。如果x为矩阵A对应的特征向量，则有：$Ax=\lambda x$。即对特征向量x做矩阵A对应的线性变换的效果是：向量方向不变，仅长度伸缩λ 倍！

      • 例如$A=\left[\begin{array}{cc}3& -1\\ -1& 3\end{array}\right]$,求得它的特征向量和特征值为$$\begin{gathered} v_1=[\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}{]}^T,{\lambda }_1=2 \\ {v}_2=[-\frac{\sqrt{2}}{2},\frac{\sqrt{2}}{2}{]}^T,{\lambda }_2=4 \end{gathered}$$.

      • 

      • 例如对于计算Ax，其中x=[0,1]，先将x分解到两个特征向量上：$V^{T}x=[v_1,v_2{]}^T[0,1{]}^T$.

      • 

      • 然后在两个特征向量方向上分别进行伸缩变换，有：$\sum (V^{T}x)=\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right]([v_1,v_2{]}^T\left[\begin{array}{c}0\\ 1\end{array}\right])$.

      • 

      • 最后再进行简单的向量合成，可有：$V(\sum V^{T}x)=[v_1,v_2](\left[\begin{array}{cc}{\lambda }_1& 0\\ 0& {\lambda }_2\end{array}\right][v_1,v_2{]}^T\left[\begin{array}{c}0\\ 1\end{array}\right])$。

      • 

      • 一般的，对于非奇异n阶方阵，有n个特征向量和与之对应的特征值，故n阶方阵A对应的线性变换操作其实可以分解成三步：

        • 将向量x先分解到n个特征向量对应的方向上（本质是求解x在以特征向量组成的基上的表示），
        • 分别进行伸缩变换（在特征向量组成的基上进行伸缩变换），
        • 最后进行向量合成（本质是求解得到的新向量在标准基上的表示）。

      • 这其实就是在描述熟悉的矩阵特征值分解：$A=U\Sigma U^T$。

      • 特征值分解其实是对线性变换中旋转、缩放两种效应的归并，奇异值分解正是对线性变换的旋转、缩放和投影三种效应的一个析构（当V的维度大于U的维度时存在投影效应）。

      • 对于任意单位向量x，Ax的最大值(这里使用向量的2范数度量值的大小)是多少？显然，x为特征向量v2时其值最大，因为这时的x全部“投影”到伸缩系数最大的特征向量上，而其他单位向量多多少少会在v1方向上分解出一部分，在v1方向上只有2倍的伸缩，不如在v2方向上4倍伸缩的值来的更大。这样，我们可以得到一个非常重要的式子：$\frac{||Ax|{|}_2}{||x|{|}_2}=||Ax|{|}_2\le \sigma (A),其中||x|{|}_2=1$。其中σ (A)表示A的最大特征值(奇异值)，也称为A的谱范数。

• 因此，在本文中，提出了几个必要的修改，以稳定的训练动态和促进收敛的ViT为基础的GAN。

  • 在鉴别器中，重新考察了自注意的Lipschitz性质，并进一步设计了一种增强Lipschitz连续性的改进的谱归一化。与不能解决不稳定性问题的常规谱归一化不同，这些技术在稳定基于ViT的鉴别器的训练动态方面表现出高效率。

• 进行了消融研究,以验证所提出的技术的必要性及其在实现稳定和卓越的图像生成性能方面的核心作用。对于基于ViT的生成器，研究了各种架构设计，并发现了对层标准化和输出映射层的两个关键修改。实验表明，改进的基于ViT的生成器可以更好地促进基于ViT和基于CNN的鉴别器的对抗训练。

• 在三个标准图像合成基准上进行实验。本文的ViTGAN的模型大大优于之前基于Transformer的GAN模型[Two transformers can make one strong gan]，即使不使用卷积或池化，也能达到与领先的基于CNN的GAN(如StyleGAN2)相当的性能。

• 据本文所知，所提出的ViTGAN模型是GANs中利用视觉transformer的第一种方法，更重要的是，它首次在标准图像生成基准(包括CIFAR、CelebA和LSUN bedroom数据集)上展示了这种transformer与最先进的卷积架构[Large scale gan training for high fidelity natural image synthesis，Analyzing and improving the image quality of StyleGAN]相当的性能。

• GAN：在机器学习中也如此，监督学习学的是如何分析信息（如听，读），而生成模型想要解决的是怎么输出信息（如写，说）。

  • 机器学习，深度学习他们通常只在做一件事 - 分析输入，找到这个输入的一个标签。通常将这种模式称之为识别。 如果凭空让机器产生一幅画，一段曲子，用监督学习学习出来的模型，是不具备创作能力的。
  • 监督学习的训练目标是给每一个数据，找到一个正确的标签/描述/数值。模型并不想锻炼想象力。
  • 生成模型不是监督学习，它算是一种非监督学习，导致它生成的东西可能在现实世界中压根不存在。 也可以认为它这是在发挥想象力。
  • 在监督学习中，我们有一个监督信号，预测的Y和真实Y的差别就是模型的老师。在GAN中，是凭空生成一个Y。当然，这里的凭空是一个假凭空，这里的凭空指的是用想象力 X 来生成一个Y。
  • 定义一个模型，它的任务就是来判断这只想象出来的Y是不是能够拟合真正Y的分布。但是光让这个模型看想象Y，它没有参考物，也不会知道是否能够拟合真正Y的分布， 所以还要给这个模型看一些真Y，让它知道哪些是真Y，哪些是想象的Y。
  • 用这种方法来训练一个辨别模型当然是没问题的，可是最终目的是为了让生成模型生成真假难辨的想象Y， 上面的步骤貌似并不能达成这个目标，充其量，训练出了一个厉害的辨别模型。
  • 能不能将辨别模型的能力转接到生成模型呢？让辨别模型指导生成模型进化？ 这就是GAN这套框架为什么厉害的原因了。
  • GAN是一种生成网络，它通过判别器（discriminator）和生成器（generator）打配合，最终训练出一个可以无限制生成数据的模型。
  • 训练 GAN 真的是一件十分困难的事情，因为训练GAN时，生成器和判别器是一种对抗的状态， 任何一方太强，都会碾压对方，对抗的平衡被打破，训练就会失败。

Related Work

• Generative Adversarial Networks：生成对抗网络(GANs) 使用对抗学习对目标分布进行建模。通常被公式化为最小化真实数据分布和生成数据分布之间的一些距离的最小-最大优化问题，例，通过f-散度或积分概率度量(IPMs) ，如Wasserstein距离。

  • GAN模型的最大不足特点是动态训练过程中不稳定。因此，提出了许多旨在稳定训练的努力，从而确保趋同。常见的方法包括光谱归一化，梯度惩罚，一致性正则化和数据增强。这些技术都是在卷积神经网络(CNN)内部设计的，并且只在卷积GAN模型中得到验证。然而，发现这些方法不足以稳定基于transformer的GANs的训练。
  • [An empirical study of training self-supervised vision transformers]还提出一个类似的发现，是关于不同的预训练任务。这可能源于ViTs的超常能力和通过自注意力捕获与CNN不同类型的感应偏差。本文介绍新技术，以克服不稳定的对抗训练的ViT。

• Vision Transformers：视觉transformer(ViT) 是一种无卷积transformer，可对一系列图像patchs执行图像分类。ViT通过利用大规模数据集上的预训练，展示了Transformer架构相对于经典CNN的优越性。

  • DeiT 通过知识提取和正则化技巧提高了ViTs的采样效率。MLP-Mixer进一步放弃自注意力，代之以MLP来混合每个位置的特征。与此同时，ViT已经扩展到各种计算机视觉任务，如对象检测，视频中的动作识别，多任务预训练。本文的工作是最先在GAN模型中利用视觉transformer生成图像的工作之一。

• Generative Transformer in Vision：受GPT-3的成功推动，一些试点工作通过自回归学习或图像和文本之间的跨模态学习来研究使用转换器的图像生成。这些方法不同于本文的方法，因为它们将图像生成建模为自回归序列学习问题。相反，本文的工作在生成性对抗训练范式中训练视觉变形者。

  • 最接近我们的工作是TransGAN，提出了一个纯粹的transformer为基础的GAN模型。虽然提出了多任务协同训练和本地化初始化以实现更好的训练，但TransGAN忽略了训练稳定性的关键技术，其性能远远低于领先的卷积GAN模型。凭借本文的设计，本文首次证明了基于transformer的GAN与基于CNN的最新GAN模型相比，能够实现具有竞争力的性能。

• f-散度

  • 在概率统计中，f散度是一个函数，这个函数用来衡量两个概率密度p和q的区别，也就是衡量这两个分布多么的相同或者不同。p和q是同一个空间中的两个概率密度函数。f散度具有非负性

    • $$D_f(p||q)=\int q(x)f\frac{p(x)}{q(x)}dx\ge f(\int q(x)\frac{p(x)}{q(x)}dx)=f(1)=0$$

  • 它们之间的f散度可以用如下方程表示：$D_f(p||q)=\int q(x)f\frac{p(x)}{q(x)}dx$。f函数满足两个条件：f函数是一个凸函数，并且f(1)=0。如果f(x)=xlogx，那就是KL散度。如果是f(x)=-logx，那就表示reverse KL散度。

• 积分概率度量IPMs

  • 将损失函数分为基于积分概率度量（IPM）的损失函数和基于非积分概率度量的损失函数。在基于IPM的GANs中，判别器被限制在一个特定的函数类，例如WGAN中的鉴别器被限制在1-Lipschitz。基于非IPM的GANs中的判别器没有这样的约束。

• Consistency Regularization

  • Consistency Regularization 的主要思想是：对于一个输入，即使受到微小干扰，其预测都应该是一致的。
  • 其实很多代价都有这个内涵，如 MSE 代价，最小化预测与标签的差值，也就是希望预测与标签能够一致。如 KL 散度、交叉熵代价也类似。所以一致性，是一种非常内在而本质的目标，可以让深度网络进行有效学习。

• 协同训练 Co-training

  • Co-training 是基于分歧的方法，其假设每个数据可以从不同的角度（view）进行分类，不同角度可以训练出不同的分类器，然后用这些从不同角度训练出来的分类器对无标签样本进行分类，再选出认为可信的无标签样本加入训练集中。
  • 由于这些分类器从不同角度训练出来的，可以形成一种互补，而提高分类精度；就如同从不同角度可以更好地理解事物一样。
  • 协同训练法要求数据具有两个充分冗余且满足条件独立性的视图：
    • “充分（Sufficient）” 是指每个视图都包含足够产生最优学习器的信息, 此时对其中任一视图来说，另一个视图则是“冗余（Redundant）” 的；
    • 对类别标记来说这两个视图条件独立。

Preliminaries: Vision Transformers (ViTs)

• Vision Transformer是一个用于图像分类的纯Transformer架构，它对一系列图像patchs进行操作。在raster scan之后，2D图像$x\in R^{H\times W\times C}$被展平成一系列图像片，表示为$x_p\in R^{L\times (P^2\cdot C)}$,其中$L=\frac{H\times W}{P^2}$是有效序列长度，P × P × C是每个图像片的尺寸。

  • 光栅扫描(RasterScan)是指从左往右，由上往下，先扫描完一行，再移至下一行起始位置继续扫描。

    • 光栅扫描是利用水平线构造图像的一种方法。这些线可以是图像的模拟表示，也可以是像素序列，其中每个点代表图像的一个小矩形区域。光栅扫描技术的主要应用之一是在传统显示设备中一些计算机打印机也使用类似的方法在纸上构建图像。大多数数字图像文件也使用光栅扫描技术进行存储和重建。

  • Z字形扫描(Z-Scan)中Z是形象的表示方式，图像如下：

    • 

• 遵循BERT，将可学习的分类嵌入$x_{class}$与添加的1D位置嵌入$E_{pos}$一起预先添加到图像序列，以形成patch embedding h0。ViT的架构严格遵循Transformer架构。

  • $$\begin{gathered} h_0=[x_{class};x_p^{1}E;x_p^{2}E;...x_p^{L}E]+E_{pos},E\in R^{（P^2\cdot C）\ast D},E_{pos}\in R^{L+1}\ast D(1) \\ {h}_l^{‘}=MSA(LN(h_{l-1}))h_{l-1},l=1,\dots \dots ,L(2) \\ {h}_l=MLP(LN(h_l^{‘}))+h_l^{‘},l=1,\dots \dots ,L(3) \\ y=LN(h_L^0)(4) \end{gathered}$$

  • 等式2应用多头自注意力机制(MSA)。给定对应于查询、关键字和值表示的可学习矩阵Wq、Wk、Wv，通过下式计算单个自我注意头(用h索引):

    • $$Attentio{n}_h(X)=softmax(\frac{Q{K}^T}{\sqrt{d_h}})V,（5）$$

  • 其中Q = XWq，K = XWk，V = XWv。多头自注意力机制通过连接和线性投影聚集来自H个自注意力机制的信息，如下所示:

    • $$MSA(X)=conca{t}_{h=1}^H[Attentio{n}_h(X)]W+b(6)$$

Method

• 下图示出了具有ViT鉴别器和基于ViT的生成器的所提出的ViTGAN的架构。本文发现直接使用ViT作为鉴别器会使训练变得不稳定。在生成器和鉴别器中引入技术来稳定训练动态并促进收敛:(1)ViT鉴别器上的正则化和(2)生成器的新结构。

  • 
  • 提议的ViTGAN框架概述。发生器和鉴别器都是基于Vision Transformer(ViT)设计的。鉴别器分数从分类嵌入中导出(在图中表示为[*])。生成器基于块嵌入逐块生成像素。

• Regularizing ViT-based discriminator

  • 增强Transformer鉴别器的Lipschitz连续性在GAN鉴别器中起着关键作用。它首先作为一个条件引起注意，以接近WGAN中的Wasserstein距离，后来在Wasserstein损失之外的其他GAN设置中得到证实。特别地，证明了Lipschitz鉴别器保证了最佳鉴别函数的存在以及唯一Nash均衡的存在。

  • 然而，最近的一项工作[The lipschitz constant of self-attention]表明，标准点积自注意力(即上等式5)层的Lipschitz常数可以是无界的，这使得在ViTs中违反了Lipschitz连续性。为了增强ViT鉴别器的Lipschitzness特性，采用了 lipschitz self-attention中提出的L2注意力。如下面等式7所示，本文用欧几里德距离替换点积相似性，并且还将query和key自注意力的投影矩阵的权重联系起来:

    • $$Attentio{n}_h(X)=softmax(\frac{d(X{W}_q,X{W}_k)}{\sqrt{d_h}})X{W}_v,where{W}_q=W_k(7)$$

  • Wq、Wk和Wv分别是query、key和value的投影矩阵。d(·，·)计算两组点之间的矢量化L2距离。√dh是每个头部的特征尺寸。当用于GAN鉴别器时，这种修改提高了transformer的稳定性。

• Improved Spectral Normalization.

  • 为了进一步加强Lipschitz连续性，还在鉴别器训练中应用了频谱归一化(SN) 。标准SN使用幂迭代来估计神经网络中每一层的投影矩阵的谱范数。

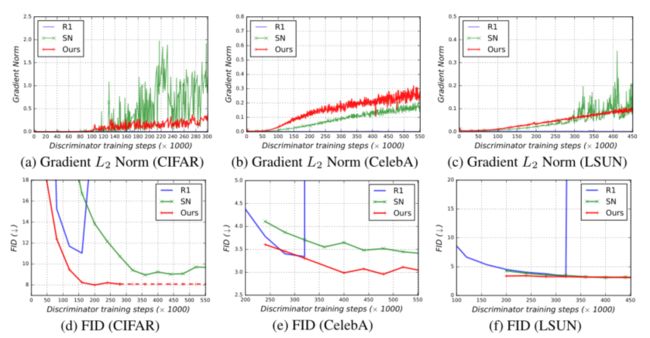
  • 然后，它用估计的谱范数除权重矩阵，因此得到的投影矩阵的Lipschitz常数等于1。我们发现transformer块对Lipschitz常数的尺度敏感，并且当使用SN时，训练表现出非常缓慢的进展(参见表3b)。类似地，本文发现当使用基于ViT的鉴别器时，R1梯度惩罚削弱了GAN训练(参见下图)。

    • 

  • [Attention is not all you need: Pure attention loses rank doubly exponentially with depth.]表明，MLP块的small Lipschitz常数可能导致transformer的输出崩溃到秩-1矩阵。为了解决这个问题，本文建议增加投影矩阵的谱范数。

  • 本文发现在初始化时将每层的归一化权重矩阵与谱范数相乘足以解决这个问题。具体来说，使用以下更新规则进行频谱归一化，其中σ计算权重矩阵的标准频谱范数:

    • $${\bar{W}}_{ISN}(W):=\sigma (W_{init})\cdot W/\sigma (W)$$

• Overlapping Image Patches.

  • ViT鉴别器由于超强学习能力而容易过拟合。本文的鉴别器和生成器使用相同的图像表示，根据预定义的网格P × P将图像划分为一系列不重叠的小块。这些任意的网格分区，如果不仔细调整，可能会促使鉴别器记住局部线索，并停止为生成器提供有意义的损失。
  • 使用一个简单的技巧来减轻这个问题，允许图像补丁之间有一些重叠。对于补丁的每个边界边缘，我们将其扩展o个像素，从而得到有效的补丁大小(P + 2o) × (P + 2o)。
  • 这导致序列具有相同的长度，但对预定义的网格不太敏感。它还可以让transformer更好地了解哪些是当前patch的相邻面片，从而提供更好的位置感。

• Generator Design

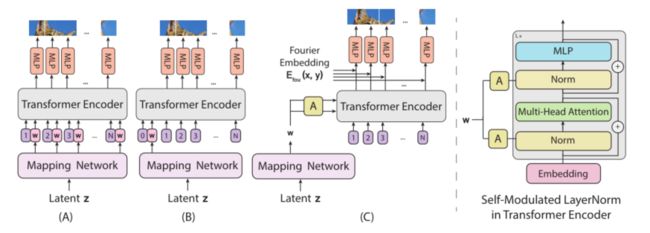
  • 设计一个基于ViT架构的生成器是一项艰巨的任务。一个挑战是将ViT从预测一组类别标签转换为在空间区域上生成像素。在介绍本文的模型之前，先讨论两个可能的基线模型，如下图 (A)和 (B)所示。

    • 
    • Generator Architectures.(A)将中间潜在嵌入w添加到每个位置嵌入中，(B)将w预先添加到序列中

  • 两个模型交换ViT的输入和输出，以从嵌入中生成像素，具体地，从通过MLP从高斯噪声向量z导出的潜在向量w中生成像素，即，w = MLP(z)(称为映射网络)。两个基线发生器的输入序列不同。上图(A)将位置嵌入序列作为输入，并将中间潜在向量w添加到每个位置嵌入中。上图(B)预先考虑了具有潜在向量的序列。这种设计的灵感来自于反转ViT，其中w用于代替等式4中嵌入$h_L^0$的分类。

  • 为了生成像素值，在两个模型中学习线性投影$E\in R^{D\times (P^{2}C)}$,以将D维输出嵌入映射到形状为P ×P ×C的图像块。$L=\frac{h\times W}{P^2}$图像块的序列$[x_p^i{]}_{i=1}^L$最终被整形以形成整个图像x。

  • 与基于CNN的生成器相比，这些baseline transformers表现不佳。根据ViT的设计原理提出了一种新颖的生成器。本文的ViTGAN发生器如下图 ©所示，由两部分组成:(1)transformer模块和(2)输出映射层。

    • 
    • ©用通过从w学习的仿射变换(在图中表示为A)计算的self-modulated layernorm形态(SLN)代替归一化

  • $$\begin{gathered} h_0=E_{pos},E_{pos}\in R^{L\ast D}(9) \\ {h}_l^{‘}=MSA(SLN(h_{l-1},w))+h_{l-1},l=1,...,L,w\in R^D(10) \\ {h}_l=MLP(SLN(h_l^{‘},w))+h_l^{‘},l=1,...,L(11) \\ y=SLN(h_L,w)=[y^1,...,y^L],y^1,...,y^L\in R^D(12) \\ x=[x_p^1,...,x_p^L]=[f_{\theta }(E_{fou},y^1),...,f_{\theta }(E_{fou},y^L)]x_p^i\in R^{P^2\ast C},x\in R^{H\ast W\ast C}(13) \end{gathered}$$

  • Self-modulated LayerNorm

    • 本文不是将噪声矢量z作为输入发送给ViT，而是使用z来调制等式10中的layernorm运算。这被称为自调制[On self modulation for generative adversarial networks]，因为调制不依赖于外部信息。等式10中的自调制层波形(SLN)通过下式计算:

      • $$SLN(h_l,w)=SLN(h_l,MLP(z))={\gamma }_l(w)\odot \frac{h_l-\mu }{\delta }+{\beta }_l(w)(14)$$

      • 其中μ和σ跟踪层内总输入的均值和方差，${\gamma }_l$和${\beta }_l$计算自适应归一化参数，该参数由从z导出的潜在向量控制。$\odot$是基于元素的点积。

  • Implicit Neural Representation for Patch Generation.

    • 本文使用隐式神经表示来学习从嵌入$y_i\in R^D$的patch到patch像素值$x_p^i\in R^{P^2\times C}$的连续映射，当与傅立叶特征或正弦激活函数结合时，隐式表示可以将生成的样本空间约束到平滑变化的自然信号空间。具体来说，类似于[Image generators with conditionally-independent pixel synthesis]，$x_p^i=f_{\theta }(E_{fou}，y_i)$其中$E_{fou}\in R^{P^{2}D}$是P× P空间位置的傅立叶编码，fθ(·，·)是2层MLP。本文还发现隐式表示对于使用基于ViT的生成器训练gan特别有帮助。
      • 
      • Generator Ablation Studies.NeurRep表示隐含的神经表征。（表3a）
    • 值得注意的是，生成器和鉴别器可以具有不同的图像网格，从而具有不同的序列长度。当将本文的模型缩放到更高分辨率的图像时，通常只增加鉴别器的序列长度或特征维数就足够了。

Experiments

• Experiment Setup

  • 数据集。CIFAR-10数据集是图像生成的标准基准，包含50K训练图像和10K测试图像。在50K图像上计算初始得分(IS) 和Fréchet Inception Distance (FID) 。

  • LSUN bedroom数据集是一个大规模图像生成基准，由300万张训练图像和300张用于验证的图像组成。在这个数据集上，由于验证集很小，所以根据训练集计算FID。

  • CelebA数据集包括162，770张未标记的人脸图像和19，962张测试图像。

  • 默认情况下，在CIFAR数据集上生成32×32个图像，在其他两个数据集上生成64×64个图像。

  • Implementation Details.

    • 对于32×32分辨率，本文使用基于4块ViT的鉴别器和基于4块ViT的发生器。对于64×64分辨率，本文将块的数量增加到6。
    • 遵循ViT-Small，所有Transformer 模块的输入/输出特征尺寸为384，MLP隐藏尺寸为1536。与[An image is worth 16x16 words: Transformers for image recognition at scale]不同，本文选择注意头的数量为6。
    • 本文还发现增加头的数量并不能改善GAN训练。对于32×32分辨率，使用4×4的patch大小，产生64个patch的序列长度。对于64×64分辨率，简单地将patch大小增加到8×8，保持与32×32分辨率相同的序列长度。
    • 以0.8的概率应用平移、颜色、剪切、缩放数据增强。所有基于transformers的基准GAN模型，包括本文的模型，都使用平衡一致性正则化(bCR),λreal =λfake = 10.0。除了bCR，本文不采用通常用于训练vit的正则化方法，如下降、权重衰减或随机深度。
    • 类似于bCR的LeCam正则化提高了性能。但是为了更清楚地消融，不包括LeCam正则化。本文使用Adam训练本文的模型，${\beta }_1=0.0，{\beta }_2=0.99，$学习率为0.002，遵循[Analyzing and improving the image quality of StyleGAN.]的实践。此外，本文采用非饱和逻辑损失，生成器权重的指数移动平均，以及均衡学习率。使用128的小批量。
    • ViTGAN和StyleGAN2都基于Tensorflow 2实现。在谷歌云TPU v2-32和v3-8上训练本文的模型。

  • 平衡一致正则化(balanced Consistency Regularization, bCR）

    • 一致正则化主要表明，使用在相同输入图像中的两组增强，应该产生相同的输出。将一致正则化条件添加到判别器损失中，并将判别器一致性强制使用在真实图像和生成图像中，而训练生成器的时候则不使用增强操作和一致性损失操作。
    • bCR这一方法通过令判别器对在一致正则化（CR）条件下的增强效果视而不见，从而有效地对判别器进行了泛化。
    • 平衡一致性正则化（bCR）提出了应用于同一输入图像的两组扩增应产生相同的输出，为判别器损失上添加一致性正则项，也为真实图像和生成的图像实施判别器一致性，而训练生成器时则不应用增强或一致性损失，这部分直观的理解如下图a所示。然而，bCR中生成器可以自由生成包含扩充的图像而不会受到任何惩罚。
      • 
    • 与bCR相似也是对输入到判别器的图像应用了增强。但是，该方法并没有使用单独的CR损失项，而是仅使用增强图像来评估判别器，并且在训练生成器时也要这样做（上图b）。

  • 使用IS（inception score）和FID（Fréchet Inception Distance）这两个指标来评价不同的GAN模型。

    • IS（inception score）：衡量GAN网络的两个指标（生成图片的质量和多样性）

      • 熵（entropy）可以用来描述随机性：如果一个随机变量是高度可预测的，那么它就有较低的熵；相反，如果它是高度不可预测，那么它就用较高的熵。

      • 在GAN中，希望条件概率P(y|x)可以被高度预测（x表示给定的图片，y表示这个图片包含的主要物体），也就是希望它的熵值较低。

      • 因此，使用inception network（可以理解这是一个固定的分类网络）来对生成的图像进行分类。然后预测P(y|x)， 这里的 y 就是标签。用这个概率来反应图片的质量。

      • 假如inception network能够以较高的概率预测图片中包含的物体，也就是有很高的把握对其进行正确分类，这就说明图片质量较高。相反，比如我们人眼并无法看出这张图片是什么，就说明这个图片质量不高。

      • 对于图像生成的多样性而言，${\int }_{z}p(y|x=G(z))dz$​,G(z) 就是生成器用噪声 z 得到的输出图像。如果生成的图像多样化很好，那么预测的标签 y 的分布则会有较高的熵，因为数量多了，就更难准确预测 y 。

      • 结合以上两个指标来说，生成图像的目标应该就是这样的：

        • 图片质量：针对每一张生成的图片，已知的分类器应该很确信的知道它属于哪一类。而这可以用条件概率 p(y|x)来表示，它越大越好。而p(y∣x)熵应该是越小越好。
        • 图片的多样性：这时候考虑的是标签的分布情况，希望标签分布均匀，而不希望模型生成的都是某一类图片。这时候考虑的不是条件概率了，而是边缘概率，也就是p(y)，展开来写应该是$p(y_1),p(y_2),...,p(y_n)$这里的n就是原训练数据的类数。希望$p(y_1)=p(y_2)=...=p(y_n)=1/n$从熵的角度来说，希望p(y)的熵越大越好。

      • 为了综合两个指标，使用KL-divergence 并用下面的公式计算得到IS的值：

        • $$IS(G)=e^{E_{x\in p^{D_{KL}(p(y|x)||p(y))}}}$$

        • x~Pg ：表示从生成器中生图片。

        • p(y|x) ：把生成的图片 x 输入到 Inception V3，得到一个 1000 维的向量 y ，也就是该图片属于各个类别的概率分布。IS 提出者的假设是，对于清晰的生成图片，这个向量的某个维度值格外大，而其余的维度值格外小（也就是概率密度图十分尖）。

        • p(y) ：N 个生成的图片（N 通常取 5000），每个生成图片都输入到 Inception V3 中，各自得到一个自己的概率分布向量，把这些向量求一个平均，得到生成器生成的图片全体在所有类别上的边缘分布

        • $D_{KL}$:对 p(y|x) 和 p(y) 求 KL 散度。KL 散度离散形式的公式如下：$D_{KL}(P||Q)={\sum }_{i}P(i)log\frac{P(i)}{Q(i)}$。

    • Fréchet Inception Distance（FID）

      • 计算 IS 时只考虑了生成样本，没有考虑真实数据，即 IS 无法反映真实数据和样本之间的距离，IS 判断数据真实性的依据，源于 Inception V3 的训练集

      • FID距离计算真实样本，生成样本在特征空间之间的距离。首先利用Inception网络来提取特征，然后使用高斯模型对特征空间进行建模，再去求解两个特征之间的距离，较低的FID意味着较高图片的质量和多样性。

      • 相比较IS来说，FID对噪声有更好的鲁棒性。因为FID只是把 Inception V3 作为特征提取器，并不依赖它判断图片的具体类别，因此不必担心 Inception V3 的训练数据和生成模型的训练数据不同。同时，由于直接衡量生成数据和真实数据的分布之间的距离，也不必担心每个类别内部只产生一模一样的图片这种形式的 mode collapse。

      • GAN的论文中经常使用FID作为IS的补充，特别是在多样性和mode collapse问题上，FID有更好地评价表现，但也有和IS同样的缺陷，比如不适合在内部差异较大的数据集上使用，无法区分过拟合等。

      • $$FID(x,g)=||{\mu }_x-{\mu }_g|{|}_2^2+Tr({\Sigma }_x+{\Sigma }_g-2({\Sigma }_x{\Sigma }_g{)}^{\frac{1}{2}})$$

        • Tr 表示矩阵对角线上元素的总和，矩阵论中俗称“迹”（trace）。均值为 μ 协方差为 Σ 。此外x表示真实的图片，g 是生成的图片。

      • 较低的FID意味着两个分布之间更接近，也就意味着生成图片的质量较高、多样性较好。

      • FID更适合描述GAN网络的多样性。同样的，FID和IS都是基于特征提取，也就是依赖于某些特征的出现或者不出现。但是他们都无法描述这些特征的空间关系。

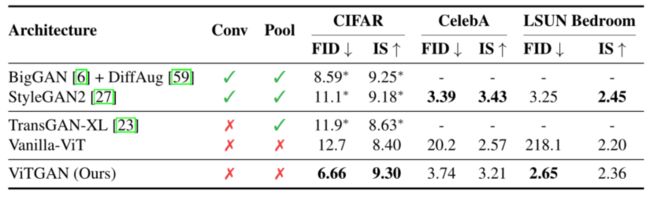
• Main Results

  • 下表显示了图像合成的三个标准基准的主要结果。本文的方法与以下基线架构进行了比较。TransGAN是唯一一款完全基于transformer架构的现有无卷积GAN。
    • 
    • Comparison to representative GAN architectures on unconditional image generation benchmarks.
    • 在无条件图像生成基准上与代表性GAN架构进行比较。*表示原始论文的结果。所有其他结果都是我们的复制。“Conv”和“Pool”分别代表卷积和池化(即下采样)。↓表示越低越好。↑表示越高越好。
  • 比较了其最佳变体TransGAN-XL。Vanilla-ViT是一种基于ViT的GAN，采用上图 (A)所示的生成和普通ViT判别器。**为了公平比较，该基线使用了 R1 penalty和bCR + DiffAug。**在Generator Ablation Studies.表中单独比较了具有上图 (B)中所示的发生器的架构。此外，BigGAN和StyleGAN2也是基于CNN的最新GAN模型。
  • 本文的ViTGAN模型远远优于其他基于transformer的GAN模型。这是由于transformer架构上的改进的稳定GAN训练，如图下所示。
    • 
    • (a-c)ViT鉴别器的梯度幅度(所有参数的L2范数)和(d-f) FID分数(越低越好),作为训练迭代的函数。
    • ViTGAN与Vanilla ViT鉴别器的两个基线进行了比较，这两个基线具有R1惩罚和谱范数(SN)。其余的架构对于所有方法都是相同的。
    • 本文的方法克服了梯度幅度的尖峰，并实现了显著更低的FID(即在CIFAR和CelebA上)或相当的FID(即在LSUN上)。这里的所有实验都是在6块ViTGAN发生器网络上进行的，分辨率为32×32。
  • **它实现了与最先进的基于CNN的模型相当的性能。**这个结果提供了一个经验证据，transformer架构可能在生成对抗训练中与卷积网络竞争。
  • 如下图所示，最佳transformer基线(中间一行)的图像保真度已经被所提出的ViTGAN模型(最后一行)显著提高。即使与StyleGAN2相比，ViTGAN生成的图像也具有相当的质量和多样性。
    • 
  • 请注意，transformer和CNN生成的图像之间似乎存在可察觉的差异，例如在CelebA图像的背景中。定量结果和定性比较证实了所提出的ViTGAN作为基于transformer的GAN模型的有效性。
    • 
    • Qualitative Comparison.在CIFAR-10 32 × 32、CelebA 64 × 64和LSUN Bedroom 64 × 64数据集上将ViTGAN与StyleGAN2以及我们的最佳transformer基线(一对普通ViT生成器和鉴别器)进行了比较。
      • 

• Ablation Studies

  • 本文在CIFAR数据集上进行消融实验，以研究关键技术的贡献并验证VitGAN模型中的设计选择。

  • Compatibility with CNN-based GAN

    • 混合搭配了ViTGAN和领先的基于CNN的GAN: StyleGAN2的生成器和鉴别器。借助StyleGAN2发生器，ViTGAN鉴别器的性能优于普通ViT鉴频器。此外，ViTGAN发生器仍然与StyleGAN2鉴别器一起工作。结果表明所提出的技术与基于transformer和基于CNN的发生器和鉴别器都兼容。
      • 
      • Comparison of transformer-based GANs on CIFAR-10.即使与CNN发生器或鉴别器配对，混合ViTGAN仍然可以在CIFAR-10上获得相当的性能。所有模型都用bCR + DiffAug 训练。

  • Generator architecture

    • 表3a显示了三种不同生成器架构下的GAN性能，如下图所示。图(B)的表现不如其他架构。
      • 
      • Generator Architectures.上图显示了本文考虑的三种生成器架构:(A)将中间潜在嵌入w添加到每个位置嵌入中，(B)将w预先添加到序列中，以及©用通过学习仿射变换(图中表示为A)从w计算的自调制层形式(SLN)替换归一化。在右侧，显示了在transformer模块中应用的self-modulation operation 的细节。
    • 本文发现图 (A)工作得很好，但是由于其不稳定性而落后于图2 ©。关于小块嵌入和像素之间的映射，使用隐式神经表示(在表3a中表示为NeurRep)似乎总是比线性映射更好。这一实验证实了本文的主张，即隐式神经表征有利于用基于ViT的发生器训练gan。

  • Discriminator regularization

    • 下表验证了技术的必要性。首先，本文比较了不同正则化方法下GAN的性能。在R1惩罚下用ViT鉴别器训练GANs非常不稳定，有时会导致完全训练失败(如下表第1行IS=NaN所示)。谱归一化优于R1惩罚。
    • 但是SN仍然表现出高方差梯度，因此遭受低质量分数。本文的L2+ISN正则化显著提高了稳定性并因此获得最好的IS和FID分数。另一方面，重叠贴片是一个简单的技巧，可以进一步改进L2+ISN方法。然而，重叠补片本身并不能很好地工作。上述结果验证了这些技术在实现ViTGAN模型的最终性能中的重要作用。
      • 
      • Discriminator Ablation Studies.‘Aug.’, ‘Reg.’, and ‘Overlap’ 分别代表DiffAug + bCR、正则化方法和重叠图像补片。

Conclusion

• 本文引入了ViTGAN，利用了GANs中的视觉transformer(vit),并提出了确保其训练稳定性和改善其收敛性的基本技术。
• 在标准基准(CIFAR-10、CelebA和LSUN bedroom)上的实验表明，所提出的模型实现了与最先进的基于CNN的GANs相当的性能。关于限制，ViTGAN是一种新的通用GAN模型，构建在vanilla ViT架构上。
• 它仍然无法击败最好的基于CNN的GAN模型，该模型采用了多年来开发的复杂技术。这可以通过将先进的训练技术(例如[22，45])纳入ViTGAN框架来改善。
• 希望ViTGAN可以促进该领域的未来研究，并可以扩展到其他图像[Image-to-image translation with conditional adversarial networks.，Dual contradistinctive generative autoencoder]和视频[Train sparsely, generate densely: Memory-efficient unsupervised training of high-resolution temporal gan.，Regularizing generative adversarial networks under limited data.]合成任务。