A Gentle Introduction to Graph Neural Networks
本文是跟李沐读论文的笔记,这篇介绍了A Gentle Intorduction to Graph Neural Netoworks这篇文章。
文章目录
-
-
- 1.引言
- 2.什么是图
-
- 举例
- 3.与图结构相关的一些问题
-
- graph-level task
- Node-level task
- Edge-level task
- 图在机器学习中的挑战
- 4.Graph Neural Networks
- 5.GNN PlayGround
- 6.相关知识
-
- Other types of graphs (multigraphs, hypergraphs, hypernodes, hierarchical graphs)
- Sampling Graphs and Batching in GNNS
- Comparing aggregation operations
- GCN as subgraph function approximators
- Edges and Graph Dual
- Graph convolutions as matrix multiplications, and matrix multiplications as walks on a graph
- Graph Attention Networks
- Graph explanations and attributions
- Generative modelling
-
1.引言
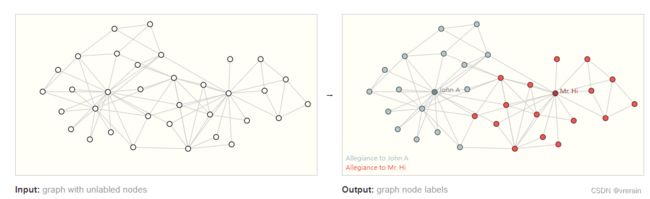
本文介绍了GNN,GNN已经有了很多领域的应用,例如:antibacterial discovery(抗生素发现) , physics simulations(物理模拟), fake news detection(假新闻检测), traffic prediction(流量预测) 和推荐系统等领域。
如下图所示,图神经网络可以表示很多的信息。

本文共分为四部分,首先介绍了哪些数据更容易表示成图数据,讲了一些例子。其次我们探索了图结构数据和其它类型数据的不同,以及使用图数据时,我们不得不做的一些选择。然后我们介绍了一个GNN的模型。最后我们提供了一个GNN playground,可以在上面进行一些实验。
2.什么是图

从上图中可以看出,图代表了节点之间的关系,由三部分组成分别是V、E、U,VE分别代表点和边,U表示整个图的信息。无向图和有向图的区别。
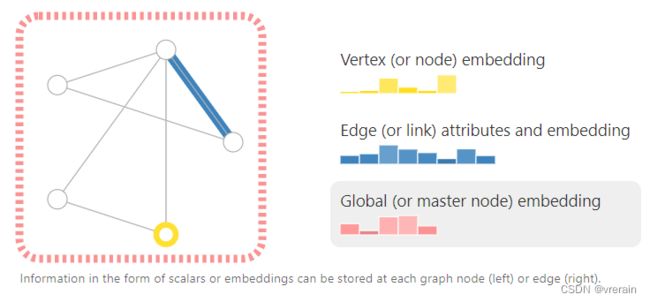
我们可以在VEG上存储不同的信息,例如上图所示,利用embedding来表示信息。
举例
image as graphs

从上图可以看出,image由一些像素点组成,每个像素点的位置用xy坐标表示,我们用邻接矩阵来表示这个结构,如果有有颜色,就代表有连接。
social network as graphs

citation network as graph
Machine learning models, programming code and math equations同样可以表示成图。
3.与图结构相关的一些问题
在图上的预测任务中有三种类型,分别是graph-level、edge-level、node-level。
在图级任务中,我们预测整个图的单个属性。对于节点级任务,我们预测图中每个节点的某些属性。对于边级任务,我们希望预测图形中边的属性或存在。
graph-level task
Node-level task
Edge-level task

边级推理的一个例子是图像场景理解。除了识别图像中的对象之外,深度学习模型还可用于预测它们之间的关系。我们可以将其表述为边级分类:给定表示图像中对象的节点,我们希望预测这些节点中的哪些节点共享一条边或该边的值是什么。如果我们希望发现实体之间的联系,我们可以考虑完全连接的图,并根据它们的预测值修剪边以得到稀疏图。
图在机器学习中的挑战
图大概有四类信息,节点信息、边信息、图信息和连接信息。对于前三种信息很容易表示,对于连接信息,有多种表示方式一种就是邻接矩阵,矩阵也很方便进行计算,但是邻接矩阵是个系数矩阵,占用的空间较大,并且当变换点的排列顺序时(如AB,BA),相同的图会产生不同的邻接矩阵,这不能保证深度学习会有相同的输出。另一种表示方式是邻接链表。表示如下图所示。Nodes表示节点的信息,Edges表示边的信息。Adjacency List表示连接的信息。Global表示图的信息。

4.Graph Neural Networks
GNN 是对图的所有属性(节点、边、全局上下文)的可优化转换,可保留图形对称性(排列不变性)。
以MLP为例,图之间通过MLP进行连接,利用MLP对图的UVE进行更新。由于GNN不会更新输入图的连通性,因此我们可以使用与输入图相同的邻接列表和相同数量的特征向量来描述GNN的输出图。但是,输出图已更新embedding,因为GNN已更新每个节点,边缘和全局上下文表示。
对于预测任务,GNN采用Pooling information来实现预测,二分类、回归任务、多分类任务都可以实现。

例如,图形中的信息可能存储在边缘中,但节点中没有信息,但仍需要在节点上进行预测。我们需要一种方法从边缘收集信息,并将其提供给节点进行预测。我们可以通过池化来做到这一点。池化过程分为两个步骤:
- 对于要合并的每个项目,收集其每个嵌入并将其连接到矩阵中。
- 然后,通常通过求和运算聚合收集的嵌入。
.
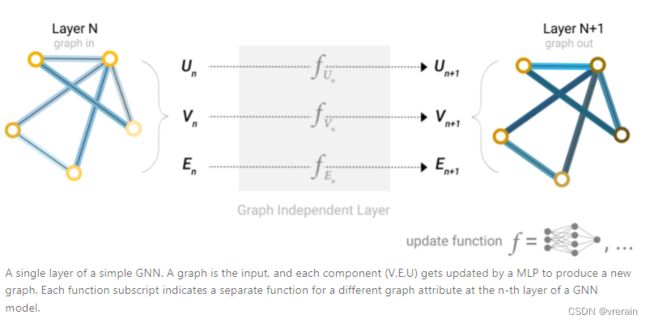
只有边的信息,做节点的预测

只有节点的信息,做边的预测
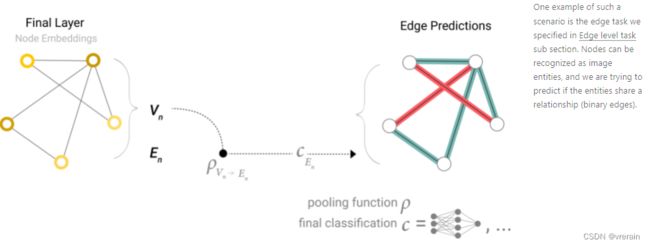
只有节点信息,对图进行预测
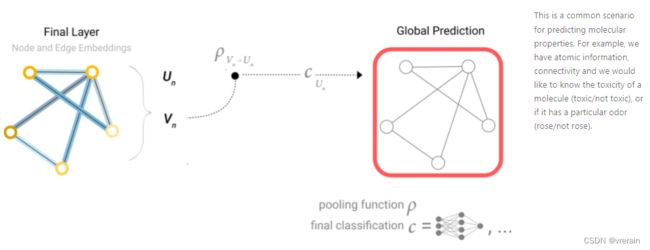
在我们的示例中,分类模型c可以很容易地用任何可微分模型替换,或者使用广义线性模型适应多类分类。下图是最简单的GNN的完整示意图。请注意,在这个最简单的GNN公式中,我们根本没有在GNN层内使用图形的连通性。每个节点都是独立处理的,每个边以及全局上下文也是如此。我们仅在汇集信息进行预测时使用连接。
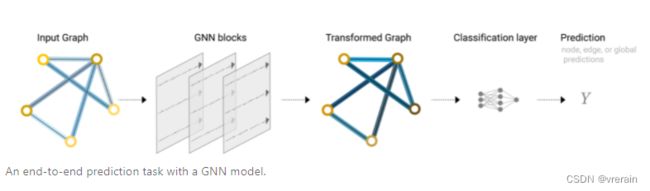
消息传递分为三个步骤:
- 对于图中的每个节点,收集所有相邻节点嵌入(或消息),即g。
- 通过聚合函数(如 sum)聚合所有消息。
- 所有池化消息都通过更新函数传递,通常是学习的神经网络。
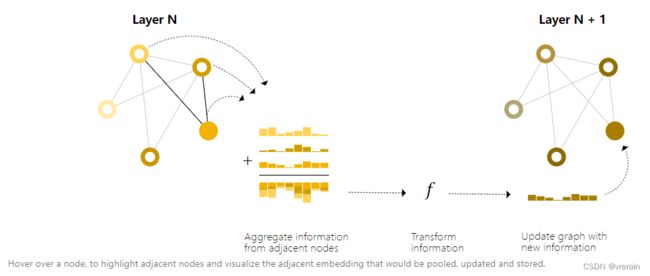
这让人想起标准卷积:从本质上讲,消息传递和卷积是聚合和处理元素邻居的信息以更新元素值的操作。在图形中,元素是一个节点,在图像中,元素是一个像素。但是,图形中相邻节点的数量可以是可变的,这与图像中不同,在图像中,每个像素都有一定数量的相邻元素。
通过将消息传递GNN层的消息堆叠在一起,节点最终可以合并整个图形中的信息:在三层之后,节点具有距离它三步之遥的节点的信息。更新过程如下图所示(只有边的信息时,信息从边传到节点)。

同理,只有节点的信息时,我们也可以将信息从节点传到边。
下面是一些其它的更新方式
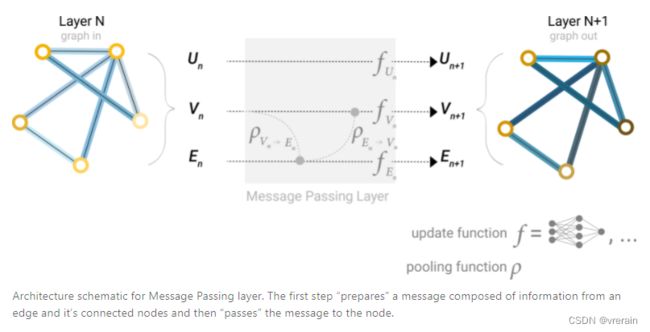

到目前为止,我们描述的网络存在一个缺陷:图中彼此相距较远的节点可能永远无法有效地将信息相互传输,即使我们多次应用消息传递。对于一个节点,如果我们有 k 层,信息最多会传播 k 步远。如果预测任务依赖于相距很远的节点或节点组,则这可能是一个问题。一种解决方案是让所有节点都能够相互传递信息。不幸的是,对于大型图形,这很快就会变得计算昂贵。
此问题的一种解决方案是使用图 (U) 的全局表示形式,该图有时称为主节点或上下文向量。这个全局上下文向量连接到网络中的所有其他节点和边缘,并且可以充当它们之间的桥梁来传递信息,从而为整个图形构建表示。这创建了比本来可以学习的更丰富,更复杂的图形表示形式。
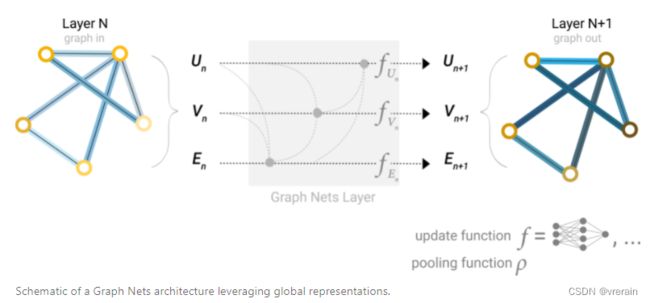
5.GNN PlayGround
详见原文。
也介绍了一些参数低于模型的影响。
6.相关知识
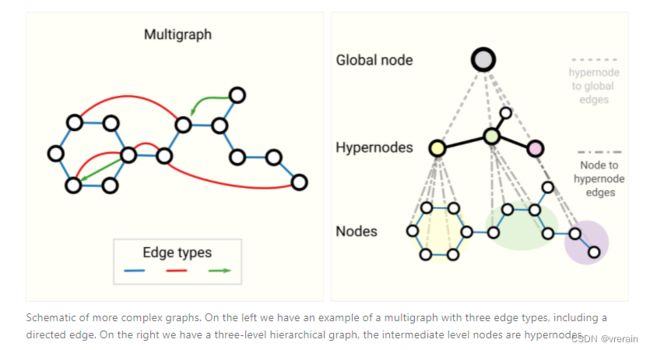
Other types of graphs (multigraphs, hypergraphs, hypernodes, hierarchical graphs)
Sampling Graphs and Batching in GNNS
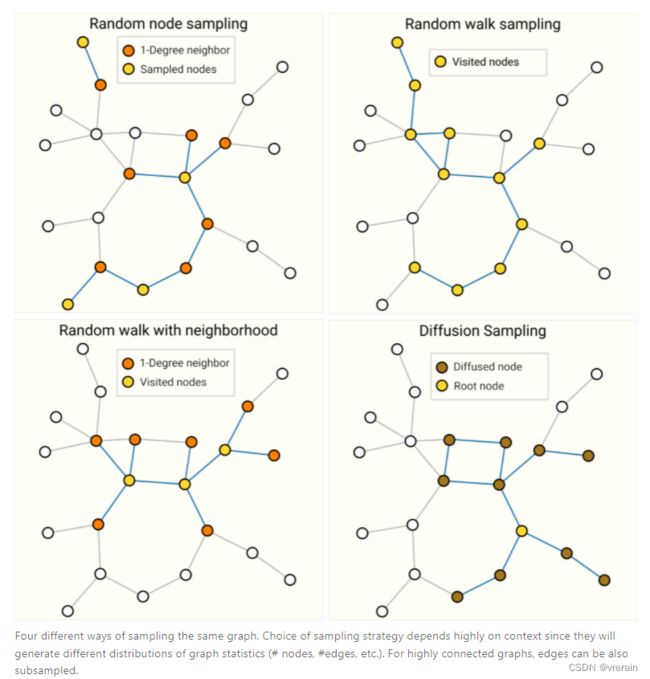
训练神经网络的常见做法是使用根据训练数据的随机常数大小(批大小)子集(小批量)计算的梯度来更新网络参数。这种做法对图形提出了挑战,因为彼此相邻的节点和边的数量存在差异,这意味着我们不能具有恒定的批大小。使用图形进行批处理的主要思想是创建子图,以保留较大图形的基本属性。此图形采样操作高度依赖于上下文,并涉及从图形中子选择节点和边缘。这些操作在某些上下文中(引用网络)可能是有意义的,而在另一些上下文中,这些操作可能太强了(分子,其中子图仅表示新的,较小的分子)。如何对图形进行采样是一个开放的研究问题。如果我们关心在邻域级别保留结构,一种方法是随机抽样一个统一数量的节点,即我们的节点集。然后添加与节点集相邻的距离为 k 的相邻节点,包括它们的边。每个邻域都可以被视为一个单独的图形,并且GNN可以在这些子图的批次上进行训练。可以屏蔽损失以仅考虑节点集,因为所有相邻节点都具有不完整的邻域。更有效的策略可能是首先随机抽样单个节点,将其邻域扩展到距离k,然后在扩展集中选择另一个节点。一旦构建了一定数量的节点、边或子图,就可以终止这些操作。如果上下文允许,我们可以通过选择初始节点集,然后对恒定数量的节点进行子采样(例如随机,或通过随机游走或Metropolis算法)来构建恒定大小的邻域。
Comparing aggregation operations
聚合方式有多种,例如Max, Mean, Sum。没有最佳方式。设计聚合是一个开放性的研究问题。
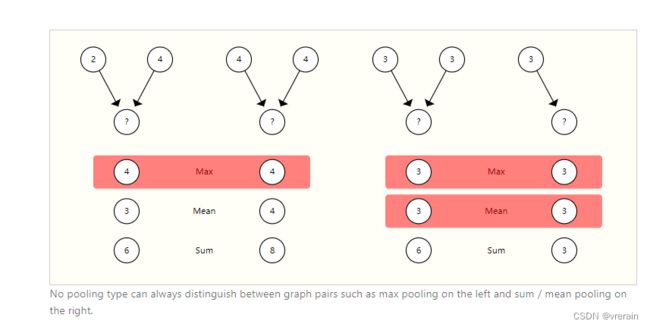
GCN as subgraph function approximators
当聚焦于一个节点时,在 k 层之后,更新的节点制图表达具有所有相邻要素的有限视点,直至 k 距离,本质上是子图表示。边缘表示也是如此。
因此,GCN正在收集大小为k的所有可能的子图,并从一个节点或边缘的有利位置学习向量表示。可能的子图的数量可以组合增长,因此从头开始枚举这些子图,而不是像GCN那样动态构建它们,可能会令人望而却步。

Edges and Graph Dual
需要注意的一件事是,边缘预测和节点预测虽然看似不同,但通常归结为同一个问题:图形上的边缘预测任务。G可以表述为节点级预测G的双重。
获取G的对偶,我们可以将节点转换为边缘(并将边缘转换为节点)。图及其对偶包含相同的信息,只是以不同的方式表示。有时,此属性使得在一种表示中解决问题比在另一种表示中更容易,例如傅里叶空间中的频率。简而言之,要解决边缘分类问题G,我们可以考虑在 上做图卷积G的对偶(这与学习上的边缘表示相同)G),这个想法是用双原始图卷积网络开发的
CNN的假设是:空间变换的不变性
RNN的假设是:时序的延续性
GNN的假设是:图的对称性