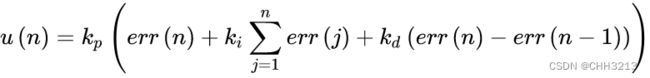模型预测控制(MPC)
文章目录
- 参考资料
- 1. 基本概念
-
- MPC vs PID
- MPC vs optimal control
- MPC优点
- 2. MPC整体流程
-
- 预测区间与控制区间
- 约束
- MPC流程
- 3. MPC设计
- 4. MPC应用——无人车轨迹跟踪
-
- 无人车轨迹跟踪建模
- python实现(待续。。)
- 5. MPC开源库/程序
参考资料
- bilibili的DR_CAN讲解的MPC模型预测控制器
- 知乎上一个比较通俗易懂的解释
- 模型预测控制
- 轨迹跟踪模型预测控制(MPC)原理与python实现
- DR_CAN笔记MPC
- MPC控制笔记
1. 基本概念
-
模型预测控制(MPC)的核心思想就是以优化方法求解最优控制器,其中优化方法大多时候采用二次规划(Quadratic Programming)。
-
MPC控制器优化得到的控制输出也是系统在未来有限时间步的控制序列。 当然,由于理论构建的模型与系统真实模型都有误差,所以,实际上更远未来的控制输出对系统控制的价值很低,故MPC仅执行输出序列中的第一个控制输出。
模型
分为机理模型和基于数据的模型(例如用神经网络训练的一个model)使用基于数据的模型的MPC可以结合model based RL使用。
预测
模型就是用来预测的,预测的目的是为了更好的决策
控制
控制即决策,根据预测来作出决策。
MPC vs PID
我们都明白,PID是万能的(手动狗头),现在工业用得最广的控制器也是PID。
PID控制器分为位置式和增量式,位置式控制律一般可以写为:
从该控制律中我们可以看到PID的两个问题:
-
PID控制器不具有“前瞻性”:参与计算的各个量,有当前的 err ,上个控制周期的 err,以及之前所有的err累计和,但没有未来的 err。
-
PID属于无模型控制。仅通过err控制进行控制器设计
反观MPC,它利用一个已有的模型、系统当前的状态和未来的控制量,来预测系统未来的输出,然后与我们期望的系统输出做比较,得到一个损失函数(代价函数),即:
损 失 函 数 = ( 未 来 输 出 ( 模 型 , 当 前 状 态 , 未 来 控 制 量 ) − 期 望 输 出 ) 2 损失函数 = (未来输出(模型,当前状态,未来控制量)-期望输出)^2 损失函数=(未来输出(模型,当前状态,未来控制量)−期望输出)2
由于上式中模型、当前状态、期望输出都是已知的,因此只有未来控制量一个自变量。采用二次规划的方法求解出某个未来控制量,使得损失函数最小,前面提到,这个未来控制量的第一个元素就是当前控制周期的控制量。
MPC vs optimal control
最优控制(optimal control)指的是在一定的约束情况下达到最优状态的系统表现,其中约束情况通常是实际环境所带来的限制,例如汽车中的油门不能无限大等。
最优控制强调的是“最优”,一般最优控制需要在整个时间域上进行求优化(从0时刻到正无穷时刻的积分),这样才能保证最优性,这是一种很贪婪的行为,需要消耗大量算力。同时,系统如果是一个时变系统,或者面临扰动的话,前一时刻得到的最优并不一定是下一时刻的最优值。
J = ∫ 0 ∞ E T Q E + U T R U d t J=\int_{0}^{\infty} E^{T} Q E+U^{T} R U d t J=∫0∞ETQE+UTRUdt
最优控制常用解法有: 变分法,极大值原理,动态规划。
MPC仅考虑未来几个时间步,一定程度上牺牲了最优性。
MPC优点
-
模型预测控制善于处理多输入多输出系统(MIMO);
对于MIMO系统,PID需要为每个子系统单独设计PID控制器,由于存在耦合对于较大的系统难以实现
-
模型预测控制可以处理约束,如安全性约束,上下阈值;
-
模型预测控制是一种向前考虑未来时间步的有限时域优化方法(一定的预测能力)
最优控制要求在整个时间优化
实际上模型预测控制采用了一个折中的策略,既不是像最优控制那样考虑整个时域,也不是仅仅考虑当前,而是考虑未来的有限时间域。
2. MPC整体流程
预测区间与控制区间
对于一般的离散化系统(因为实际计算机实现的控制系统都是离散的系统,连续系统可以进行离散化操作),在k时刻,我们可以测量出系统的当前状态 y ( k ) y(k) y(k),再通过计算得到的 u ( k ) , u ( k + 1 ) , u ( k + 2 ) . . . u ( k + j ) u(k),u(k+1),u(k+2)...u(k+j) u(k),u(k+1),u(k+2)...u(k+j)得到系统未来状态的估计值 y ( k + 1 ) , y ( k + 2 ) . . . y ( k + j ) y(k+1),y(k+2)...y(k+j) y(k+1),y(k+2)...y(k+j);
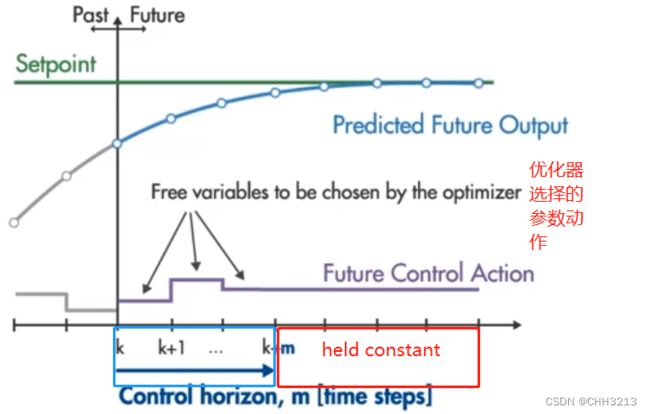
将预测状态估计的部分称为预测区间(Predictive Horizon),指的是一次优化后预测未来输出的时间步的个数。
将控制估计的部分称为控制区间(Control Horizon),在得到最优输入之后,我们只施加当前时刻的输入u(k),即控制区间的第一位控制输入。
如下图 [ k , k + m ] [k, k+m] [k,k+m]范围为控制区间,之后的红色部分称为 held constant,其中控制区间是要通过优化器来进行优化的参数。
过小的控制区间,可能无法做到较好的控制,而较大的控制区间,比如与预测区间相等,则会导致只有前一部分的控制范围才会有较好的效果,而后一部分的控制范围则收效甚微,而且将带来大量的计算开销。
约束
对于约束,一般分为Hard约束和Soft约束,Hard约束是不可违背必须遵守的,在控制系统中,输入输出都可能会有约束限制,但是在设计时不建议将输入输出都给予Hard约束,因为这两部的约束有可能是有重叠的,导致优化器会产生不可行解。
Hard约束不能违反,Soft约束可以;比如Hard约束是刹车踩的幅度;Soft约束是速度
建议输出采用Soft约束,而输入的话建议输入和输入参数变化率二者之间不要同时为Hard约束,可以一个Hard一个Soft。
MPC流程
模型预测控制在k时刻共需三步;
-
第一步:获取系统的当前状态;
-
第二步:基于 u ( k ) , u ( k + 1 ) , u ( k + 2 ) . . . u ( k + j ) u(k),u(k+1),u(k+2)...u(k+j) u(k),u(k+1),u(k+2)...u(k+j)进行最优化处理;
离散系统的代价函数可以参考
J = ∑ k j − 1 E k T Q E k + u k T R u k + E N T F E N J=\sum_{k}^{j-1}E_k^TQE_k+u_k^TRu_k+E_N^TFE_N J=k∑j−1EkTQEk+ukTRuk+ENTFEN
其中 E N E_N EN表示误差的终值,也是衡量优劣的一种标准。
-
第三步:只取 u ( k ) u(k) u(k)作为控制输入施加在系统上。
在下一时刻重复以上三步,在下一步进行预测时使用的就是下一步的状态值,我们将这样的方案称为滚动优化控制(Receding Horizon Control)。
3. MPC设计
当模型是线性的时候(非线性系统可以线性化),MPC的设计求解一般使用二次规划方法。
设线性模型为以下形式:
x k + 1 = A x k + B u k + C (1) x_{k+1}=Ax_k+Bu_k+C \tag{1} xk+1=Axk+Buk+C(1)
假定未来 T T T步的控制输入已知,为 u k , u k + 1 , u k + 2 , . . . , u k + T u_k, u_{k+1}, u_{k+2}, ..., u_{k+T} uk,uk+1,uk+2,...,uk+T,根据以上模型与输入,我们可以计算未来 T T T步的状态:
x k + 1 = A x k + B u k + C x_{k+1}=Ax_k+Bu_k+C xk+1=Axk+Buk+C
x k + 2 = A x k + 1 + B u k + 1 + C = A ( A x k + B u k + C ) + B u k + 1 + C = A 2 x k + 1 + A B u k + B u k + 1 + A C + C x_{k+2}=Ax_{k+1}+Bu_{k+1}+C=A(Ax_k+Bu_k+C)+Bu_{k+1}+C=A^2x_{k+1}+ABu_k+Bu_{k+1}+AC+C xk+2=Axk+1+Buk+1+C=A(Axk+Buk+C)+Buk+1+C=A2xk+1+ABuk+Buk+1+AC+C
x k + 3 = A 3 x k + A 2 B u k + A B k + 1 + B u k + 2 + A 2 C + A C + C . . . x_{k+3}=A^3x_k+A^2Bu_{k}+AB_{k+1}+Bu_{k+2}+A^2C+AC+C\\ ... xk+3=A3xk+A2Buk+ABk+1+Buk+2+A2C+AC+C...
x k + T = A T x k + A T − 1 B u k + A T − 2 B u k + 1 + . . . + A T − i B u k + i − 1 + . . . + B u k + T − 1 + A T − 1 C + A T − 2 C + . . . + C x_{k+T}=A^{T}x_{k}+A^{T-1}Bu_k+A^{T-2}Bu_{k+1}+...+A^{T-i}Bu_{k+i-1}+...+Bu_{k+T-1}+A^{T-1}C+A^{T-2}C+...+C xk+T=ATxk+AT−1Buk+AT−2Buk+1+...+AT−iBuk+i−1+...+Buk+T−1+AT−1C+AT−2C+...+C
将上面 T T T步写成矩阵向量形式:
X = A x k + B u + C (2) \mathcal{X}=\mathcal{A}x_k+\mathcal{B}\mathbf{u}+\mathcal{C} \tag{2} X=Axk+Bu+C(2)
其中,
X = [ x k + 1 , x k + 2 , x k + 3 , . . . x k + T ] T \mathcal{X}=\left[x_{k+1}, x_{k+2}, x_{k+3},...x_{k+T}\right]^T X=[xk+1,xk+2,xk+3,...xk+T]T
u = [ u k , u k + 1 , u k + 2 , . . . , u k + T − 1 ] T \mathbf{u}=\left[u_k,u_{k+1},u_{k+2},...,u_{k+T-1}\right]^T u=[uk,uk+1,uk+2,...,uk+T−1]T
A = [ A , A 2 , A 3 , . . . , A T ] T \mathcal{A}=\left[A, A^2 ,A^3 ,... ,A^T\right]^T A=[A,A2,A3,...,AT]T
B = ( 0 0 . . . 0 B 0 . . . 0 A B B . . . 0 . . . . . . . . . . . . A T − 1 B A T − 2 B . . . B ) \mathcal{B}=\begin{pmatrix}0&0&...&0\\ B&0&...&0\\ AB&B&...&0\\ ...&...&...&...\\ A^{T-1}B&A^{T-2}B&...&B\end{pmatrix} B=⎝⎜⎜⎜⎜⎛0BAB...AT−1B00B...AT−2B...............000...B⎠⎟⎟⎟⎟⎞
C = [ C A C + C A 2 C + A C + C … A k + T − 1 C + … + C ] \mathcal{C}=\left[\begin{array}{c} C \\ A C+C \\ A^{2} C+A C+C \\ \ldots \\ A^{k+T-1} C+\ldots+C \end{array}\right] C=⎣⎢⎢⎢⎢⎡CAC+CA2C+AC+C…Ak+T−1C+…+C⎦⎥⎥⎥⎥⎤
上式 B \mathcal{B} B中的下三角形式,直接反映了系统在时间上的因果关系,即 k + 1 k+1 k+1时刻的输入对 k k k 时刻的输出没有影响, k + 2 k+2 k+2 时刻的输入对 k k k 和 k + 1 k+1 k+1 时刻没有影响,等等。
假定参考轨迹为 X ‾ = [ x ˉ k + 1 x ˉ k + 2 x ˉ k + 3 … x ˉ k + T ] T \overline{\mathcal{X}}=\left[\begin{array}{lllll}\bar{x}_{k+1} & \bar{x}_{k+2} & \bar{x}_{k+3} & \ldots & \bar{x}_{k+T}\end{array}\right]^{T} X=[xˉk+1xˉk+2xˉk+3…xˉk+T]T,则MPC的一个简单的目标代价函数如下:
min J = E T Q E + u T R u s.t. u m i n ≤ u ≤ u m a x (3) \min \mathcal{J}=\mathcal{E}^T Q \mathcal{E}+\mathbf{u}^T R \mathbf{u} \\ \text{s.t. } u_{min}\leq \mathbf{u}\leq u_{max} \tag{3} minJ=ETQE+uTRus.t. umin≤u≤umax(3)
其中, E = X − X ‾ = [ x k + 1 − x ˉ k + 1 x k + 2 − x ˉ k + 2 … x k + T − x ˉ k + T ] T \mathcal{E}=\mathcal{X}-\overline{\mathcal{X}}=\left[\begin{array}{llll}x_{k+1}-\bar{x}_{k+1} & x_{k+2}-\bar{x}_{k+2} & \ldots & x_{k+T}-\bar{x}_{k+T}\end{array}\right]^{T} E=X−X=[xk+1−xˉk+1xk+2−xˉk+2…xk+T−xˉk+T]T
u T R u \mathbf{u}^T R \mathbf{u} uTRu这一项是为了让控制输入不会太大,因此代价函数中添加了一项对控制量的约束。
将式(2)代入式(3),则优化变量仅剩 u \mathbf{u} u。以上最优化问题可用二次规划方法求解,得到满足目标代价函数的最优控制序列 u = { u k , u k + 1 , u k + 2 . . . u k + T − 1 } \mathbf{u}=\left\{u_k,u_{k+1},u_{k+2}...u_{k+T−1}\right\} u={uk,uk+1,uk+2...uk+T−1}。
当转换成式(3)后,可以利用凸优化库进行求解,例如python的cvxopt,OSQP: An Operator Splitting Solver for Quadratic Programs,Casdi等。
4. MPC应用——无人车轨迹跟踪
此部分来源于博客 轨迹跟踪模型预测控制(MPC)原理与python实现
无人车轨迹跟踪建模
无人车几何运动学模型如下:
x ˙ = v cos ( θ ) y ˙ = v sin ( θ ) θ ˙ = v tan ( δ ) L v ˙ = a (1) \begin{gathered} \tag{1} \dot{x}=v \cos (\theta) \\ \dot{y}=v \sin (\theta) \\ \dot{\theta}=v \frac{\tan (\delta)}{L} \\ \dot{v}=a \end{gathered} x˙=vcos(θ)y˙=vsin(θ)θ˙=vLtan(δ)v˙=a(1)
其中:
v v v为无人车的速度;
x ˙ \dot{x} x˙为无人车在世界坐标系中X轴方向上的分速度,记为 v x v_{x} vx;
y ˙ \dot{y} y˙为无人车在世界坐标系中Y轴方向上的分速度,记为 v y v_{y} vy;
θ \theta θ为无人车在世界坐标中的航向角;
θ ˙ \dot{\theta} θ˙则为无人车的角速度,可记为 ω \omega ω。
为了突显两个主要控制对象[速度 v v v与角速度 ω \omega ω],对以上无人车运动学模型进行变形,得以下形式:
[ x ˙ y ˙ θ ˙ ] = [ cos θ sin θ 0 ] v + [ 0 0 1 ] w \left[\begin{array}{l} \dot{x} \\ \dot{y} \\ \dot{\theta} \end{array}\right]=\left[\begin{array}{c} \cos \theta \\ \sin \theta \\ 0 \end{array}\right] v+\left[\begin{array}{l} 0 \\ 0 \\ 1 \end{array}\right] w ⎣⎡x˙y˙θ˙⎦⎤=⎣⎡cosθsinθ0⎦⎤v+⎣⎡001⎦⎤w
将以上连续的微分模型离散化成差分模型(假设差分间隔为 d t d_t dt):
x k + 1 = x k + v k cos ( θ k ) d t y k + 1 = y k + v k sin ( θ k ) d t θ k + 1 = θ k + v k tan ( δ k ) L d t v k + 1 = v k + a k d t cte k + 1 = c t e k + v k sin ( θ k ) d t epsi k + 1 = e p s i k + v k tan ( δ k ) L d t (2) \begin{gathered} \tag{2} x_{k+1}=x_{k}+v_{k} \cos \left(\theta_{k}\right) d_{t} \\ y_{k+1}=y_{k}+v_{k} \sin \left(\theta_{k}\right) d_{t} \\ \theta_{k+1}=\theta_{k}+v_{k} \frac{\tan \left(\delta_{k}\right)}{L} d_{t} \\ v_{k+1}=v_{k}+a_{k} d_{t} \\ \text { cte }_{k+1}=\mathrm{cte}_{k}+v_{k} \sin \left(\theta_{k}\right) d_{t} \\ \text { epsi }_{k+1}=\mathrm{epsi}_{k}+v_{k} \frac{\tan \left(\delta_{k}\right)}{L} d_{t} \end{gathered} xk+1=xk+vkcos(θk)dtyk+1=yk+vksin(θk)dtθk+1=θk+vkLtan(δk)dtvk+1=vk+akdt cte k+1=ctek+vksin(θk)dt epsi k+1=epsik+vkLtan(δk)dt(2)
假定无人车需要跟踪的轨迹是由离散点 { ( x ‾ 1 , y ‾ 1 ) , ( x ‾ 2 , y ‾ 2 ) , . . . , ( x ‾ M , y ‾ M ) } \{(\overline{x}_1, \overline{y}_1), (\overline{x}_2, \overline{y}_2),...,(\overline{x}_M, \overline{y}_{M})\} {(x1,y1),(x2,y2),...,(xM,yM)}通过三次曲线拟合而成,可表示成由 x x x为自变量的函数: y = f ( x ) = c 0 x 3 + c 1 x 2 + c 2 x + c 3 y=f(x)=c_0 x^3+c_1 x^2+c_2 x+c_3 y=f(x)=c0x3+c1x2+c2x+c3。值得说明的是,表示轨迹的离散点需要转换到车本体坐标系下。
因此,在每一预测步,我们可以根据无人车的 x k x_k xk与 y k y_k yk值计算横向跟踪误差 cte k \text{cte}_{k} ctek与航向偏差 epsi k \text{epsi}_k epsik。具体计算公式如下:
cte k = f ( x k ) − y k e p s i k = arc tan ( f ′ ( x k ) ) − θ (3) \begin{gathered} \tag{3} \operatorname{cte}_{k}=f\left(x_{k}\right)-y_{k} \\ \mathrm{epsi}_{k}=\operatorname{arc} \tan \left(f^{\prime}\left(x_{k}\right)\right)-\theta \end{gathered} ctek=f(xk)−ykepsik=arctan(f′(xk))−θ(3)
假设给定预测步长为 N N N,可以设计以下优化目标函数:
min J = ∑ k = 1 N ( ω cte ∥ cte t ∥ 2 + ω epsi ∥ epsi k ∥ 2 + ω v ∥ v k − v ref ∥ 2 ) + ∑ k = 1 N − 1 ( ω δ ∥ δ k ∥ 2 + ω a ∥ a k ∥ 2 ) + ∑ k = 1 N − 2 ( ω rate δ ∥ δ k + 1 − δ k ∥ 2 + ω rate a ∥ a k + 1 − a k ∥ 2 ) (4) \begin{aligned} \tag{4} &\min \mathcal{J}=\sum_{k=1}^{N}\left(\omega_{\text {cte }} \| \text { cte }_{t}\left\|^{2}+\omega_{\text {epsi }}\right\| \operatorname{epsi}_{k}\left\|^{2}+\omega_{v}\right\| v_{k}-v_{\text {ref }} \|^{2}\right)\\ &+\sum_{k=1}^{N-1}\left(\omega_{\delta}\left\|\delta_{k}\right\|^{2}+\omega_{a}\left\|a_{k}\right\|^{2}\right)\\ &+\sum_{k=1}^{N-2}\left(\omega_{\text {rate }_{\delta}}\left\|\delta_{k+1}-\delta_{k}\right\|^{2}+\omega_{\text {rate }_{a}}\left\|a_{k+1}-a_{k}\right\|^{2}\right) \end{aligned} minJ=k=1∑N(ωcte ∥ cte t∥∥2+ωepsi ∥∥epsik∥∥2+ωv∥∥vk−vref ∥2)+k=1∑N−1(ωδ∥δk∥2+ωa∥ak∥2)+k=1∑N−2(ωrate δ∥δk+1−δk∥2+ωrate a∥ak+1−ak∥2)(4)
满足:
动态模型约束:
s.t. x k + 1 = x k + v k cos ( θ k ) d t , k = 1 , 2 , … , N − 1 y k + 1 = y k + v k sin ( θ k ) d t , k = 1 , 2 , … , N − 1 θ k + 1 = θ k + v k tan ( δ k ) L d t , k = 1 , 2 , … , N − 1 v k + 1 = v k + a k d t , k = 1 , 2 , … , N − 1 c t e k + 1 = f ( x k ) − y k + v k sin ( θ k ) d t epsi k + 1 = arctan ( f ′ ( x k ) ) − θ + v k tan ( δ k ) L d t (5) \begin{array}{cc} \tag{5} \text { s.t. } & x_{k+1}=x_{k}+v_{k} \cos \left(\theta_{k}\right) d_{t}, k=1,2, \ldots, N-1 \\ & y_{k+1}=y_{k}+v_{k} \sin \left(\theta_{k}\right) d_{t}, k=1,2, \ldots, N-1 \\ & \theta_{k+1}=\theta_{k}+v_{k} \frac{\tan \left(\delta_{k}\right)}{L} d_{t}, k=1,2, \ldots, N-1 \\ & v_{k+1}=v_{k}+a_{k} d_{t}, k=1,2, \ldots, N-1 \\ & { }^{c t e_{k+1}}=f\left(x_{k}\right)-y_{k}+v_{k} \sin \left(\theta_{k}\right) d_{t} \\ &\text { epsi }_{k+1}=\arctan \left(f^{\prime}\left(x_{k}\right)\right)-\theta+v_{k} \frac{\tan \left(\delta_{k}\right)}{L} d_{t} \end{array} s.t. xk+1=xk+vkcos(θk)dt,k=1,2,…,N−1yk+1=yk+vksin(θk)dt,k=1,2,…,N−1θk+1=θk+vkLtan(δk)dt,k=1,2,…,N−1vk+1=vk+akdt,k=1,2,…,N−1ctek+1=f(xk)−yk+vksin(θk)dt epsi k+1=arctan(f′(xk))−θ+vkLtan(δk)dt(5)
执行器约束:
δ ∈ [ δ min , δ max ] a ∈ [ a min , a max ] (6) \begin{aligned} \tag{6} &\delta \in\left[\delta_{\min }, \delta_{\max }\right] \\ &a \in\left[a_{\min }, a_{\max }\right] \end{aligned} δ∈[δmin,δmax]a∈[amin,amax](6)
式(4)、(5)、(6)构成无人车轨迹跟踪的完整控制问题。
python实现(待续。。)
5. MPC开源库/程序
- do-mpc
- mpc.pytorch