Pytorch学习笔记（二）——自动微分

一、前言

在神经网络中，最常用到的算法就是反向传播了。我们通常需要计算损失函数相对于各个参数的梯度。如果手动去计算这些梯度项的数学表达式再用numpy去一个个实现无疑是非常麻烦的，好在pytorch提供了自动微分这一功能，使用时只需要按部就班的计算损失函数的值，再调用 backward() 方法即可计算各个参数的梯度。

考虑最简单的情形：一元线性回归，最终的模型应具有 $y=wx+b$ 的形式。不妨假设 $w=2,b=1$，我们先使用如下代码生成具有噪声的数据集，这样方便之后使用pytorch的自动微分功能来实现线性回归：

def make_regression_data(num=1000):
    x = torch.linspace(-1, 1, num)
    y = 2 * x + 1 + 0.2 * torch.randn(num)
    return x, y

回归问题的损失函数通常为均方误差，即 $\frac{1}{2}{\sum }_{i=1}^n(y_i-{\hat{y}}_i{)}^2$，代码实现如下：

def loss_func(y, y_pred):
    return torch.norm(y - y_pred, 2) ** 2 / 2

注意到我们要求的参数是 $w,b$，即每次更新参数时需要计算 $w,b$ 的梯度。我们当然可以使用链式求导法则求出 $w,b$ 梯度项的数学表达式，但接下来我们将用自动微分来更简洁地实现这一操作。

二、计算图

pytorch使用如下的计算图来计算参数的梯度项：

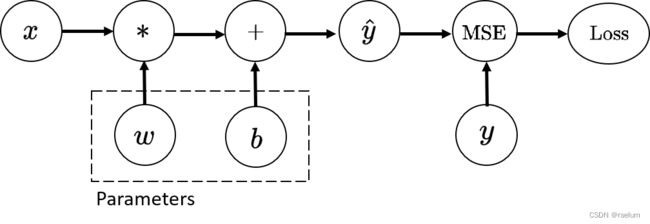
在优化过程中，我们需要求 $Loss$ 相对于 $w,b$ 的梯度，因此初始化时，我们需要将 $w,b$ 的 requires_grad 属性设置为 True。

在正向计算过程中，与 requires.grad=True 节点相关联的父节点的 requires_grad 属性都会被自动设置为 True：

torch.manual_seed(42)
x, y = make_regression_data(1000)
w = torch.rand(1, requires_grad=True)
b = torch.rand(1, requires_grad=True)
y_pred = w * x + b  # 利用广播机制
loss = loss_func(y, y_pred)

x.requires_grad
# False
y.requires_grad
# False
w.requires_grad
# True
b.requires_grad
# True
y_pred.requires_grad
# True
loss.requires_grad
# True

正向计算过后，我们可对损失函数调用 backward() 方法来反向传播计算各个梯度项，使用 grad 属性来查看各个参数的梯度：

# 计算梯度
loss.backward()
# 查看梯度
w.grad
# tensor([-614.0020])
b.grad
# tensor([-341.2478])

---

计算图实际上是一个有向无环图（DAG），所有需要更新的参数均位于叶子节点。每次执行完 backward() 后，叶子节点上的梯度会进行累加，而非叶子节点上的梯度会释放。因此每次进行参数更新后，我们需要把参数的梯度全部置为0，只需对相应的梯度项使用 zero_() 方法即可。

三、关闭梯度跟踪

默认情况下，所有设置 requires_grad=True 的张量都会跟踪它们的计算历史并且支持梯度计算。但某些情况下我们不需要这么做，例如当我们训练好了一个模型并且只想将其应用于某些输入数据时，即我们只想进行正向计算，我们可以使用 torch.no_grad() 来包住我们的计算代码以关闭梯度跟踪：

with torch.no_grad():
	# Your code...

例如，当线性回归求出 $w,b$ 后，接下来的任务就是对给定的新数据做出相应的预测，而该操作与梯度无关，因此可以关闭梯度跟踪以加快计算速度：

with torch.no_grad():
	y_pred = w * x + b

当然，我们也可以使用 detach 方法：

y_pred = w * x + b
y_pred_det = y_pred.detach()

效果是等同的。

---

一个很显然的事实是，当我们在进行参数更新时，无需跟踪梯度，因此完整的参数更新框架如下：

with torch.no_grad():
	# 参数更新
# 将参数的梯度项置为0

四、求解线性回归

# 初始化
torch.manual_seed(42)  # 设置随机种子方便复现
x, y = make_regression_data()
w = torch.rand(1, requires_grad=True)
b = torch.rand(1, requires_grad=True)
lr = 0.001  # 学习率，即步长

# 迭代2000次
for _ in range(2000):
    # 计算损失函数
    y_pred = w * x + b
    loss = loss_func(y, y_pred)
    # 计算梯度
    loss.backward()
    # 更新参数
    with torch.no_grad():
        w -= lr * w.grad
        b -= lr * b.grad
    w.grad.zero_()
    b.grad.zero_()
print(w, b)
# tensor([1.9871], requires_grad=True) tensor([1.0008], requires_grad=True)

从结果可以看出，$w=1.9871,b=1.0008$，和真实情况非常接近。