高频算法题冒险之旅精讲(一)之LeetCode小牛试刀五道题
导读:
本篇博文是LeetCode算法题讲解篇,对高频算法题进行详细而深入的讲解,解题语言选择的是Java。
更多算法专栏如下:
⛳️ 排序算法
⛳️ 分治法
⛳️ LeetCode高频算法题讲解
⛳️ 数据结构
目录
-
- ⛳️ 1.只出现一次的数字(第136题)
-
- 1.1题目:
- 1.2解题思路及完整Java代码
-
- 1.2.1用map
- 1.2.2用set
- 1.2.3用位运算
- ⛳️ 2.多数元素(第169题)
-
- 2.1题目:
- 2.2解题思路及完整Java代码
-
- 2.2.1使用map去存储元素出现的次数
- 2.2.2排序后直接输出
- 2.2.3摩尔投票法
- ⛳️ 3.搜索二维矩阵 II(第240题)
-
- 3.1题目:
- 3.2解题思路及完整Java代码
-
- 3.2.1暴力解法
- 3.2.2一般解题思路
- 3.2.3看成一棵排序二叉树
- ⛳️ 4.合并两个有序数组(第88题)
-
- 4.1题目:
- 4.2解题思路及完整Java代码
-
- 4.2.1 归并排序思想,一个新数组,两个指针,简单明了
- ⛳️ 5.鸡蛋掉落(第887题)
-
- 5.1题目
- 5.2解题思路及完整Java代码
-
- 5.2.1动态规划(二维背包)
前言:
本次算法冒险之旅将围绕LeetCode上面的算法面试题汇总进行讲解,该部分的题型在面试或笔试中出现的频率很高。
如下是本次冒险之旅的目录:
本篇文章讲解冒险之旅开始前的五道题,让大家感受一下算法的魅力,之后笔者会逐一进行讲解如下的每一章节,每一个大标题都会写一篇文章,算是对其进行剖析和详细汇总。
在进入正题之前,不妨先让我们回顾几个有意思的经典互联网公司的面试题目,热热身。
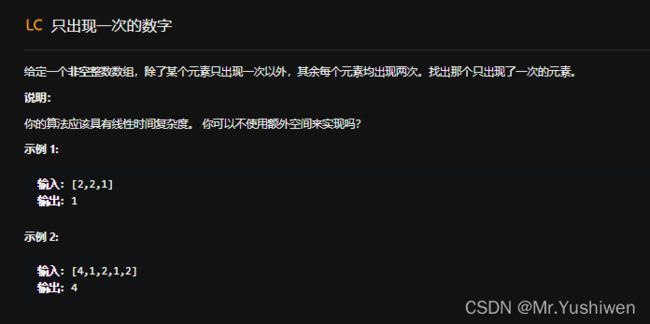
⛳️ 1.只出现一次的数字(第136题)
1.1题目:
1.2解题思路及完整Java代码
根据题目所给出的信息,我想到的map或者set去解决,因为题目中很明确说明了有且只有一个元素会出现一次,其他的都是两次。
- 用map,我们可以在第一次的时候把元素的值作为key,下标为value存进map中,然后在进行判断下一个元素是否在map中,用key去判断,containsKey方法的时间复杂度很低,原因是key被存储到hash表中,查找时是在hash表上进行查找,其时间复杂度为:最好情况便是O(1),最坏情况是O(lgn)。如果存在就从map中移除,因为重复的话只会出现两次,题目中已经明确说明了,那么最后map中所剩的最后一个元素就是唯一出现一次的元素。
- 不重复的话,我们也会考虑到用set去解决,这个我们也很容易想到,只要是添加失败的情况,就证明之前已经向set集合中添加过该元素了,我们把之前的也删掉即可,最后剩下的哪一个也是唯一出现一次的元素。
- 用位运算中的异或,如果a、b两个值不相同,则异或结果为1。如果a、b两个值相同,异或结果为0,把所有的数字都进行异或操作就能得到结果了。
1.2.1用map
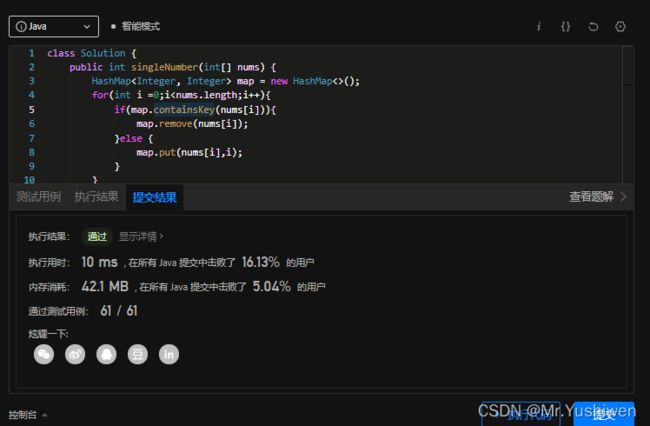
用map,我们可以在第一次的时候把元素的值作为key,下标为value存进map中,然后在进行判断下一个元素是否在map中,用key去判断,containsKey方法的时间复杂度很低,原因是key被存储到hash表中,查找时是在hash表上进行查找,其时间复杂度为:最好情况便是O(1),最坏情况是O(lgn)。如果存在就从map中移除,因为重复的话只会出现两次,题目中已经明确说明了,那么最后map中所剩的最后一个元素就是唯一出现一次的元素。
代码:
public class SingleNumber01 {
public int singleNumber(int[] nums) {
HashMap<Integer, Integer> map = new HashMap<>();
for(int i =0;i<nums.length;i++){
if(map.containsKey(nums[i])){
map.remove(nums[i]);
}else {
map.put(nums[i],i);
}
}
Object[] arr = map.keySet().toArray();
return (int) arr[0];
}
public static void main(String[] args) {
System.out.println(new SingleNumber01().singleNumber(new int[]{4, 1, 2, 1, 2}));
}
}
1.2.2用set
不重复的话,我们也会考虑到用set去解决,这个我们也很容易想到,只要是添加失败的情况,就证明之前已经向set集合中添加过该元素了,我们把之前的也删掉即可,最后剩下的哪一个也是唯一出现一次的元素。
代码:
public class SingleNumber02 {
public int singleNumber(int[] nums) {
HashSet<Integer> set = new HashSet<>();
for (int num : nums) {
if(!set.add(num))
set.remove(num);
}
Object[] arr = set.toArray();
return (int) arr[0];
}
public static void main(String[] args) {
System.out.println(new SingleNumber02().singleNumber(new int[]{4, 1, 2, 1, 2}));
}
}
执行时间:
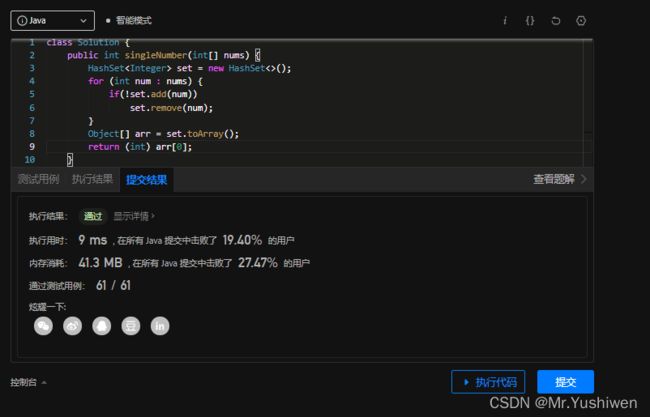
可以看到相比于第一个用map只提高了1ms,那么我们是否有更快的方法呢,此时我们i想到了用位运算。
1.2.3用位运算
用位运算中的异或,如果a、b两个值不相同,则异或结果为1。如果a、b两个值相同,异或结果为0(按位bit进行异或运算),把所有的数字都进行异或操作就能得到结果了。
代码:
public class SingleNumber03 {
public int singleNumber(int[] nums) {
int result = nums[0];
for (int i =1;i<nums.length;i++){
result=result ^ nums[i];
}
return result;
}
public static void main(String[] args) {
System.out.println(new SingleNumber03().singleNumber(new int[]{4, 1, 2, 1, 2}));
}
}
执行时间:
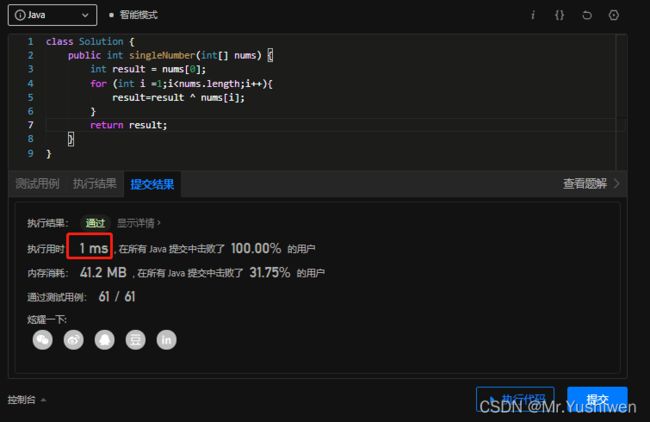
可以看到只需要1ms就执行完了,相比与前两种方法,这种方法有质的提升。
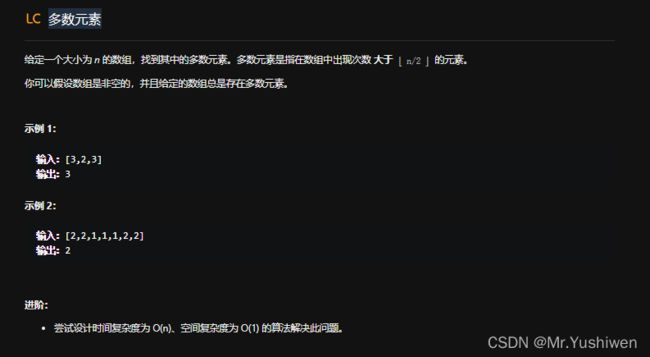
⛳️ 2.多数元素(第169题)
2.1题目:
2.2解题思路及完整Java代码
2.2.1使用map去存储元素出现的次数
- 题目中已经说明了我们可以假设数组是非空的,并且数组中总是存在多数元素,所以数组为空或者不存在多数元素的情况我们不考虑。
- 题目中对于多数元素的定义为出现次数大于n/2的元素,在元素为n的数组中,大于n/2的情况肯定只有一个数,所以我们可以断定多数元素只有一个。
- 分析到这里我们就很容易想到利用map中的key去存储元素的值,利用value进行存储元素出现的次数。
- 由于只存在一个大于n/2的数,所以我们可以在循环的过程中对map的value进行判断,如果存在大于n/2的数字那么我们把它返回即可。
代码:
public class MostElements {
public int majorityElement(int[] nums) {
HashMap<Integer, Integer> map = new HashMap<>();
for (int num : nums) {
int count = map.containsKey(num) ? map.get(num) : 0;
map.put(num,++count);
if(count>nums.length/2){
return num;
}
}
throw new RuntimeException("传入数组不符合要求!");
}
public static void main(String[] args) {
System.out.println(new MostElements().majorityElement(new int[]{2,2,1,1,1,2,2}));
}
}
执行时间:
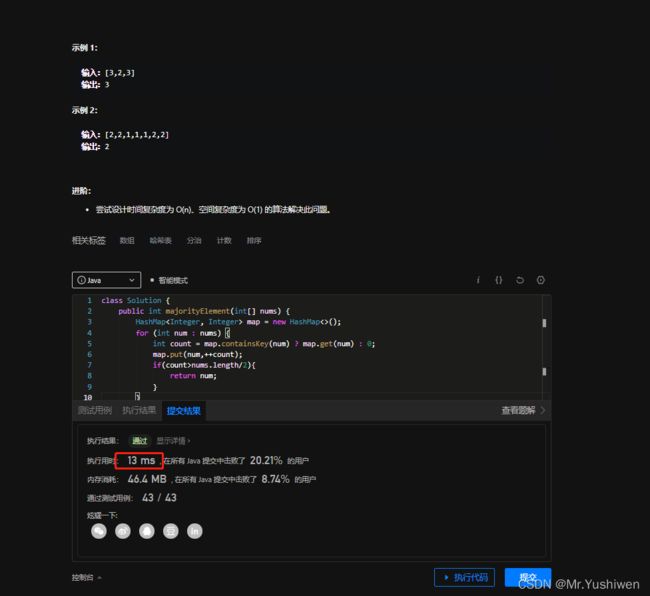
可以看到时间还是挺长的,下面我们用另外一种方法。
2.2.2排序后直接输出
我们要善于根据题意解答问题,根据题意,多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素,出现次数大于n/2,不论这个数字是最大还是最小,经过排序后,数组中间的那个元素一定是多数元素。
代码:
public class MostElements01 {
public int majorityElement(int []nums){
Arrays.parallelSort(nums);
return nums[nums.length/2];
}
public static void main(String[] args) {
System.out.println(new MostElements01().majorityElement(new int[]{2,2,1,1,1,2,2}));
}
}
执行时间:
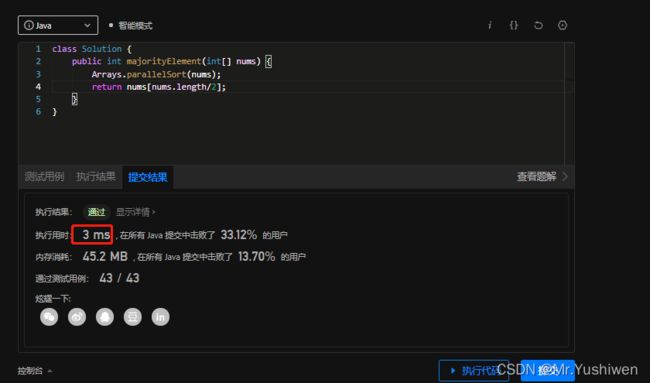
可以看到相较于之前用map进行统计,该方法所需的时间又得到了提升。那么还有其他方法使之得到进一步的提升嘛,答案是有的,我们接着看。
2.2.3摩尔投票法
理解:随机选取两个不同的数进行相消,最坏情况是,所有非多数元素于多数元素相消,因为多数元素是大于n/2的数,所以最后留下的绝对也是多数元素。
- 题目中已经说到了,数组中存在大于n/2的数;
- 定义count=0,我们可以采取刚开始选择数组中的第一个元素,count赋值等于1,然后判断数组中接下来的数是否与其相同,相同count加1,不同count减1;
- 当count等于0时,我们就选择数组中的下一个数,count赋值等于1,重复2的操作。
- 数组遍历一遍后,最后剩下的数就是多数元素了。
Java代码:
public class MostElements02 {
public int majorityElement(int[] nums) {
int major = nums[0];
for (int i = 1, count = 1; i < nums.length; i++) {
if (count == 0) {
major = nums[i];
count++;
} else if (nums[i] == major)
count++;
else
count--;
}
return major;
}
public static void main(String[] args) {
System.out.println(new MostElements02().majorityElement(new int[]{2, 2, 1, 1, 1, 2, 2}));
}
}
执行时间:
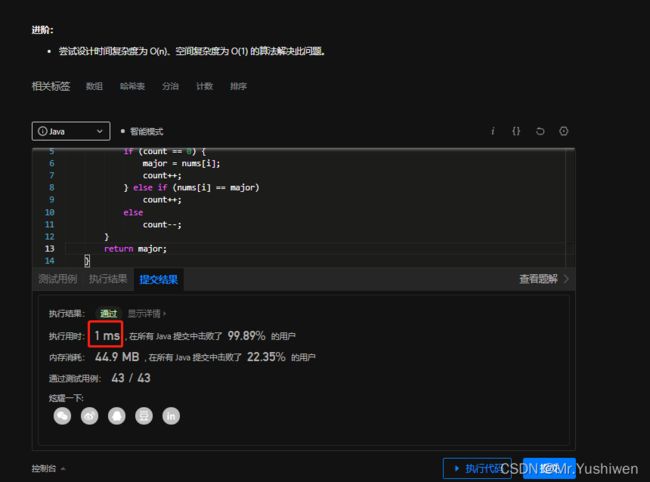
可以看到只需要1ms就执行完了,相比与前两种方法,这种方法也有质的提升,且时间复杂度是O(n)。
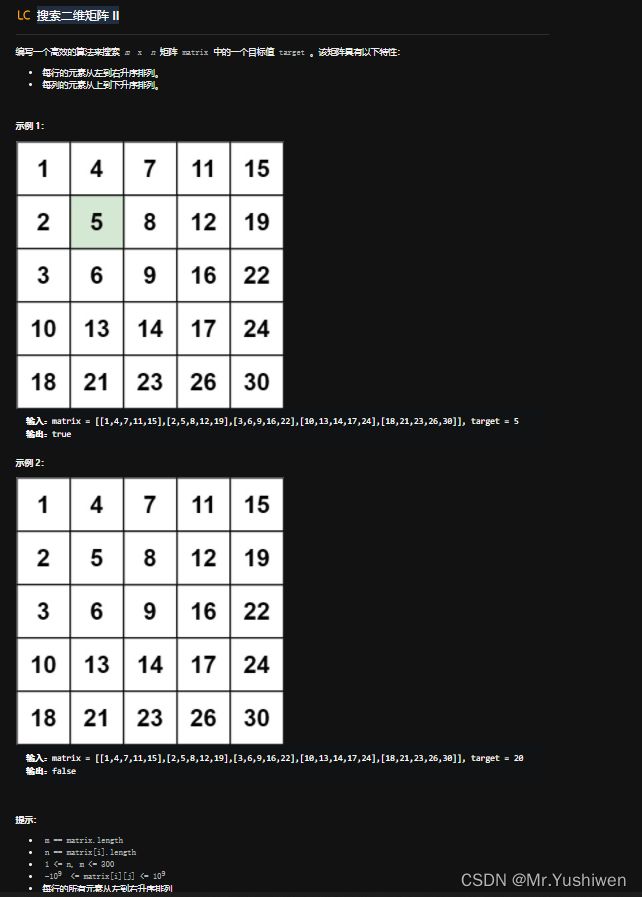
⛳️ 3.搜索二维矩阵 II(第240题)
3.1题目:
3.2解题思路及完整Java代码
3.2.1暴力解法
Java代码:
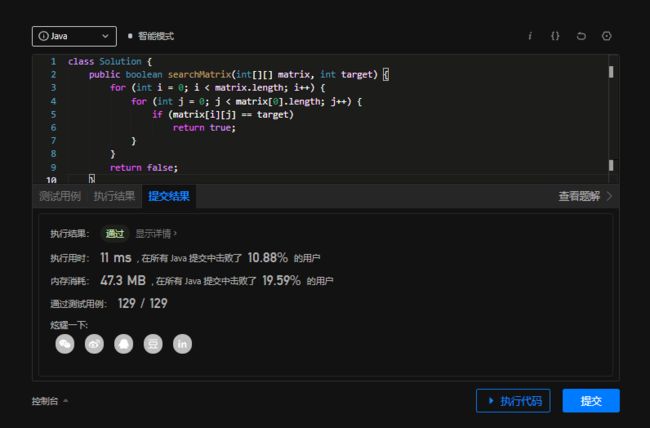
public boolean searchMatrix(int[][] matrix, int target) {
for (int i = 0; i < matrix.length; i++) {
for (int j = 0; j < matrix[0].length; j++) {
if (matrix[i][j] == target)
return true;
}
}
return false;
}
3.2.2一般解题思路
因矩阵有如下特征:
- 每行的元素从左到右升序排列。
- 每列的元素从上到下升序排列。
固很容易会想到如下解题思路;
可以看到矩阵每行的元素从左到右升序排列,
- 我们可以首先取矩阵中的第一行第一列的元素进行判断,如果矩阵当前元素比目标值小,就继续读取矩阵该行的下一个元素,然后继续和目标值作比较。如果读取到该行末尾,就读取下一行的第一个元素,直到出现2中的情况。
- 矩阵从按行读取变成按列读取:
当矩阵当前元素大于目标元素,我们就读取矩阵当前元素所在行的前一列元素,我们称之为X,读取X列的下一个元素,然后与目标值做比较,如果小于目标元素,就继续按照列读取,直到找到相等的,如果没有相等的,就把列再向前移动一位,如此循环,直到找到相等的值,当列的值等于0时,证明矩阵中不存在该元素。
Java代码:
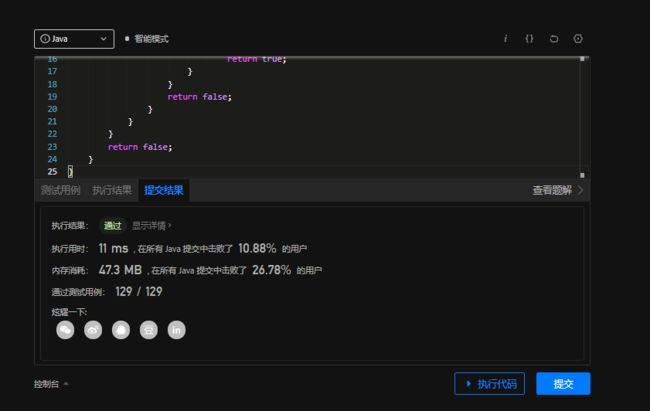
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
// 第一行先从左到右进行比较
for (int i = 0; i < matrix.length; i++) {
// 然后从上到下
for (int j = 0; j < matrix[i].length; j++) {
if (target == matrix[i][j])
return true;
if (target < matrix[i][j]) {
// 否则列减一,然后固定减一后的列,行累加进行查找,如果找到该列的行尾或者有笔目标值大的元素,就把列再向前移动一位
//当列的值等于0时,证明矩阵中不存在该元素
j--;
for(;j>=0;j--){
for (int k = i;++k < matrix.length && matrix[k][j] <= target;) {
if (matrix[k][j] == target)
return true;
}
}
return false;
}
}
}
return false;
}
}
解题时间:
3.2.3看成一棵排序二叉树
- 从矩阵的左下角开始比较(该二维数组类似于一棵排序二叉树,对于每个数来说,上方的数都小于它,右方的数都大于它,所以把左下角作为根节点开始比较)。
- 也可以从矩阵的右上角开始比较,把矩阵的右上角的元素作为二叉树的根节点。
如下以矩阵右上角为排序二叉树的根节点来举例:
Java代码:
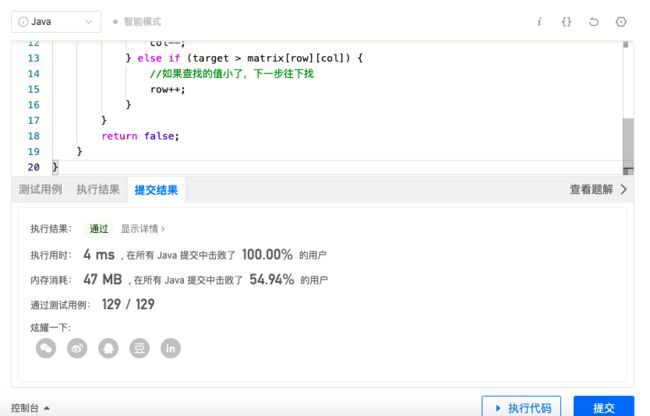
class Solution {
public boolean searchMatrix(int[][] matrix, int target) {
//从矩阵右上角开始搜索
int col = matrix[0].length - 1;
int row = 0;
while (col >= 0 && row <= matrix.length - 1) {
if (target == matrix[row][col]) {
//如果找到就直接返回
return true;
} else if (target < matrix[row][col]) {
//如果查找的值大了,下一步往左找
col--;
} else if (target > matrix[row][col]) {
//如果查找的值小了,下一步往下找
row++;
}
}
return false;
}
}
⛳️ 4.合并两个有序数组(第88题)
4.1题目:
4.2解题思路及完整Java代码
4.2.1 归并排序思想,一个新数组,两个指针,简单明了
Java代码:
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
// 题目中已说,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。
// 所以nums1足够长了
int [] arr = nums1.clone();
int index1 = 0, index2 = 0;
while (index1 + index2 < m + n) {
if(index1>=m){
nums1[index1+index2] = nums2[index2];
index2++;
}else if(index2>=n){
nums1[index1+index2] = arr[index1];
index1++;
}else if (arr[index1] <= nums2[index2]) {
nums1[index1+index2] = arr[index1];
index1++;
}else {
nums1[index1+index2] = nums2[index2];
index2++;
}
}
}
}
执行时间:
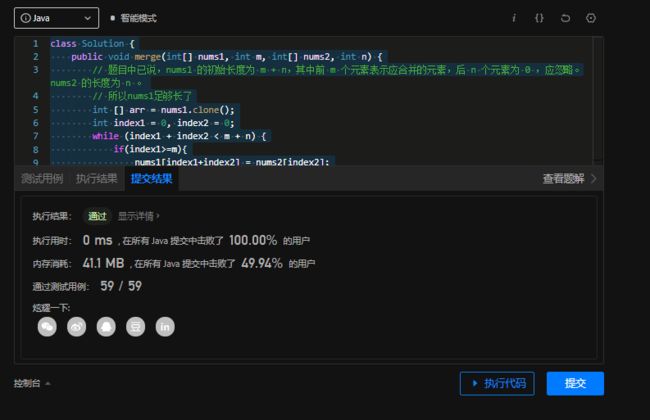
第一次就0s,就很行,哈哈哈,虽然世界效率达到了,O(m+n),但是我们还是要说一下归并排序的思路。
具体的归并排序思想可以参考笔者该篇博文:归并排序 (分而治之算法) java代码实现(java完整代码)java递归实现(分而治之)MergeSort(分治法)
⛳️ 5.鸡蛋掉落(第887题)
5.1题目
5.2解题思路及完整Java代码
这道题有点难,我们慢慢分析,
先看一个鸡蛋的时候:
- 如果你手上只有一个鸡蛋,只能从一楼开始,逐层往上试,
- 比如总共10层楼。1楼试了没碎,试2楼,直到第5层碎了,那 F=5。如果第10层还没碎,那 F=10。
- 如果非要从第7层开始试,扔下去碎了,这时只能知道 F<= 6,具体是几,因为没鸡蛋,没法试了。
- 所有一个鸡蛋的情况下,要确认F是第几层,10次一定可以试出来。即一个鸡蛋的情况下,最小次数=楼层数。
- 也就是说要考虑最坏情况
5.2.1动态规划(二维背包)
Java代码:
class Solution {
/**
01背包问题
*/
public int superEggDrop(int k, int n) {
if(n==1){
return 1;
}
//背包:鸡蛋数(k个); 物品:操作数(n个);价值:确定楼层
int[][] dp = new int[k+1][n+1];
// 有人问了,为什么不是鸡蛋作为物品,操作数作为背包?
// 背包问题往往物品与价值有正相关关系。
// 鸡蛋有k个,但实际不一定全都用上,限制一定的最小操作数,鸡蛋增加,确定楼层(价值)不一定增加
// 而取一定的鸡蛋,操作数每增加1,确定楼层(价值)就会一定增加
int count=0;
// 先遍历物品,再遍历背包
for(;dp[k][count]<n;){ // 遍历物品,这里直到价值为n就结束
count++;
for (int i = k; i >=1; i--) { // 遍历背包,二维数组可以正序或倒叙
//当前价值 = 鸡蛋碎了的价值 + 鸡蛋没碎的价值 + 确定当前层的价值1
dp[i][count] = dp[i-1][count-1]+dp[i][count-1]+1;
}
}
return count;
}
}