pytorch_lesson12 手动实现和模型实现线性回归、逻辑回归（本质是二分类）、多分类预测

提示：仅仅是学习记录笔记，搬运了学习课程的ppt内容，本意不是抄袭！望大家不要误解！纯属学习记录笔记！！！！！！

---

前言

本节课程主要内容是：手动实现回归数据、二分类数据和多分类数据的创建、神经网络的定义和反向传播，以及tensorboardX的使用。目的是为了从更深层次了解神经网络的原理。关于在item里面激活虚拟环境的命令：conda activate 项目名；查看虚拟环境的项目：conda env list；删除虚拟环境的项目：conda remove -项目名 env_name --all；退出虚拟环境命令：conda deactivate。使用pycharm的话不需要这些命令，pycharm会自动激活虚拟环境。

---

一、深度学习建模实验中数据集创建函数的创建与使用

1、 创建回归类数据函数

生成线性相关数据y=2x1- x2 + b + 扰动项

#手动生成数据
num_inputs = 2         #特征个数
num_examples = 1000    #样本个数

torch.manual_seed(420) #设置随机种子
#线性方程系数
w_true = torch.tensor([2, -1.]).reshape(2, 1)
b_true = torch.tensor(1.)
#生成特征值和标签值
features = torch.randn(num_examples, num_inputs)
labels_true = torch.mm(features, w_true) + b_true
#生成了一个y=2x_1 - x_2 + b的正相关函数
#为我们的标签增加扰动项
lables = labels_true + torch.randn(size=labels_true.shape) * 0.01

plt.subplot(121) #从左往右数的第一个1表示生成一行图片，第二个数2表示生成两列图，第三个数1表示生成第一张图
plt.scatter(features[:, 0], lables)  #查看第一个特征与标签之间的关系
plt.subplot(122)
plt.scatter(features[:, 1], lables)  #查看第二个特征与标签之间的关系
print("finish")
plt.show()

不难看出，两个特征和标签都存在一定的线性关系，并且跟特征的系数绝对值有很大关系。当然，若要增加线性模型的建模难度，可以增加扰动项的数值比例，从而削弱线性关系。

torch.manual_seed(420)
#修改因变量
lables1 = labels_true + torch.randn(size=labels_true.shape) * 2
#可视化展示
plt.subplot(221) #从左往右数的第一个1表示生成一行图片，第二个数2表示生成两列图，第三个数1表示生成第一张图
plt.scatter(features[:, 0], lables)  #查看第一个特征与标签之间的关系
plt.subplot(222)
plt.plot(features[:, 1], lables, 'ro')  #查看第二个特征与标签之间的关系

plt.subplot(223)
plt.scatter(features[:, 0], lables1)
plt.subplot(224)
plt.plot(features[:, 1], lables1, 'yo')
plt.show()

明显可以看出，当我们扰动项比较大的时候，我们的点分布得更加分散。

生成非线性的数据集，y =w x ** 2 + b +扰动项

torch.manual_seed(420)
num_inputs = 2         #特征个数
num_examples = 1000    #样本个数
w_true = torch.tensor(2.)
b_true = torch.tensor(1.)
features = torch.randn(num_examples, num_inputs)
labels_true = torch.pow(features, 2) * w_true + b_true
lables2 = labels_true + torch.randn(size=labels_true.shape) * 0.1
plt.scatter(features, lables2)
plt.show()

创建回归数据生成函数

#创建生成数据的函数
def tensorGenReg(num_examples = 1000, w = [2, -1, 1], bias = True, delta = 0.01, deg = 1):
    """回归类数据集创建函数。

    :param num_examples: 创建数据集的数据量
    :param w: 包括截距的（如果存在）特征系数向量
    :param bias：是否需要截距
    :param delta：扰动项取值
    :param deg：方程次数
    :return: 生成的特征张和标签张量
    """

    if bias == True:
        num_inputs = len(w) - 1
        features_true = torch.randn(num_examples, num_inputs)
        w_true = torch.tensor(w[:-1]).reshape(-1, 1).float()  # 自变量系数
        b_true = torch.tensor(w[-1]).float()
        if num_inputs == 1:
            lable_true = torch.pow(features_true, deg) * w_true + b_true
        else:
            lable_true = torch.mm(torch.pow(features_true, deg), w_true) + b_true
        l = torch.ones(len(features_true)).reshape(-1, 1)
        features_true = torch.cat([features_true, l], dim=1)
        labels = lable_true + torch.randn(size=(num_examples, 1)) * delta

    else:
        num_inputs = len(w)
        features_true = torch.randn(num_examples, num_inputs)
        w_true = torch.tensor(w).reshape(-1, 1).float()
        if num_inputs == 1:
            lable_true = torch.pow(features_true, deg) * w_true
        else:
            lable_true = torch.mm(torch.pow(features_true, deg), w_true)
        labels = lable_true + torch.randn(size=(num_examples, 1)) * delta
    return features_true, labels

torch.manual_seed(420)
f, l = tensorGenReg(delta=0.8)
print(f)

注：上述函数无法创建带有交叉项的方程

2、分类数据集创建方法

手动实现一个三分类数据集

torch.manual_seed(420)
num_input = 2
num_examples = 1000
#创建自变量簇
data0 = torch.normal(4, 2, size=(num_examples, num_input))  #生成均值为4，标准差为2的正太分布
data1 = torch.normal(-2, 2, size=(num_examples, num_input))
data2 = torch.normal(-6, 2, size=(num_examples, num_input))

#创建标签
label0 = torch.zeros(num_examples)
label1 = torch.ones(num_examples)
label2 = torch.full_like(label0, 2)

#合并生成最终数据
features = torch.cat((data0, data1, data2)).float()
labels = torch.cat((label0, label1, label2)).float()

plt.scatter(features[:, 0], features[:, 1], c = labels)
plt.show()

torch.manual_seed(420)
num_input = 2
num_examples = 1000
#创建自变量簇
data0 = torch.normal(4, 2, size=(num_examples, num_input))  #生成均值为4，标准差为2的正太分布
data1 = torch.normal(-2, 2, size=(num_examples, num_input))
data2 = torch.normal(-6, 2, size=(num_examples, num_input))

#创建标签
label0 = torch.zeros(num_examples)
label1 = torch.ones(num_examples)
label2 = torch.full_like(label0, 2)

# 创建自变量簇
data3 = torch.normal(3, 2, size=(num_examples, num_input))
data4 = torch.normal(0, 2, size=(num_examples, num_input))
data5 = torch.normal(-3, 2, size=(num_examples, num_input))

#合并生成最终数据
features = torch.cat((data0, data1, data2)).float()
labels = torch.cat((label0, label1, label2)).float()
features1 = torch.cat((data3, data4, data5)).float()
labels1 = torch.cat((label1, label2, label2)).long().reshape(-1, 1)

# 可视化展示
plt.subplot(121)
plt.scatter(features[:, 0], features[:, 1], c = labels)
plt.subplot(122)
plt.scatter(features1[:, 0], features1[:, 1], c = labels1)
plt.show()

创建分类数据生成函数

def tensorGenCla(num_example=500, num_input=2, num_class=3, deg_dispersion=[4, 2], bias=True):
    """分类数据集创建函数。

    :param num_examples: 每个类别的数据数量
    :param num_inputs: 数据集特征数量
    :param num_class：数据集标签类别总数
    :param deg_dispersion：数据分布离散程度参数，需要输入一个列表，其中第一个参数表示每个类别数组均值的参考、第二个参数表示随机数组标准差。
    :param bias：建立模型逻辑回归模型时是否带入截距
    :return: 生成的特征张量和标签张量，其中特征张量是浮点型二维数组，标签张量是长正型二维数组。
    """
    cluster_l = torch.empty(num_example, 1)
    mean_ = deg_dispersion[0]
    std_ = deg_dispersion[1]
    k = mean_ * (num_class-1)/2
    lf = []
    ll = []

    for i in range(num_class):
        data_temp = torch.normal(i * mean_ -k, std_, size=(num_example, num_input))
        lf.append(data_temp)
        labels_temp = torch.full_like(cluster_l, i)
        ll.append(labels_temp)

    features = torch.cat(lf).float()
    labels = torch.cat(ll).float()

    if bias == True:
        l = torch.ones(len(features)).reshape(-1, 1)
        features = torch.cat([features, l], dim=1)
    return features, labels

3、创建小批量切分函数

def data_iter(batch_size, features, labels):
    """
    数据切分函数

    :param batch_size: 每个子数据集包含多少数据
    :param featurs: 输入的特征张量
    :param labels：输入的标签张量
    :return l：包含batch_size个列表，每个列表切分后的特征和标签所组成
    """
    num_examples = len(features)
    indices = list(range(num_examples))
    random.shuffle(indices)
    l = []
    for i in range(0, num_examples, batch_size):
        j = torch.tensor(indices[i: min(i + batch_size, num_examples)])
        l.append([torch.index_select(features, 0, j), torch.index_select(labels, 0, j)])
    return l

二、PyTorch深度学习建模可视化工具TensorBoard的安装与使用

在终端输入pip install tensorboard，因为Mac的tensorboard为pytorch版本做了优化，所以不需要下载tensorboardX，接下来要进行实例化和写入数据： writer = SummaryWriter(log_dir=‘reg_loss’)，然后在epoch循环的每一批数据下面写下writer.add_scalar(‘mul’, train_l, epoch)，这样就可以查看每一轮的epoch的误差平方和的变化

writer = SummaryWriter(log_dir='reg_loss')

#训练过程
for epoch in range(num_epochs):
    for X,y in data_iter(batch_size,features,labels):
        l = loss(net(X, w), y)
        l.backward()
        sgd(w, lr)
    train_l = loss(net(features, w), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l))
    writer.add_scalar('mul', train_l, epoch)

三、深度学习基础模型建模实验

1、线性回归建模实验

手动创建实现线性回归

import random

# 绘图模块
import matplotlib as mpl
import matplotlib.pyplot as plt

# numpy
import numpy as np

# pytorch
import torch
from torch import nn,optim
import torch.nn.functional as F
from torch.utils.data import Dataset,TensorDataset,DataLoader
from torch.utils.tensorboard import SummaryWriter
from torchLearning import *

torch.manual_seed(420)
features, labels = tensorGenReg()

#建模流程
def linreg(X, w):
    return torch.mm(X, w)

#确定目标函数
def squared_loss(y_hat, y):
    num_ = y.numel()
    sse = torch.sum((y_hat.reshape(-1, 1) - y.reshape(-1, 1)) ** 2)
    return sse/ num_

#定义优化算法
def sgd(params, lr):
    params.data -= lr * params.grad
    params.grad.zero_()

#这里需要注意的是，params.data可以将参数矩阵提取出来，并在其原本结果上进行操作改变其原来的值。
#因为只要进行了backward(),w就被当作叶子节点来看待，不能在其本来的数值上进行操作，因为这会让pytorch分不清w到底是叶子节点还是中间节点

# 设置随机数种子
torch.manual_seed(420)
batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
num_epochs = 3                                 # 训练过程遍历几次数据
w = torch.zeros(3, 1, requires_grad = True)    # 随机设置初始权重

net = linreg
loss = squared_loss
writer = SummaryWriter(log_dir='reg_loss')
#训练过程
for epoch in range(num_epochs):
    for X,y in data_iter(batch_size,features,labels):
        l = loss(net(X, w), y)
        l.backward()
        sgd(w, lr)
    train_l = loss(net(features, w), labels)
    print('epoch %d, loss %f' % (epoch + 1, train_l))
    writer.add_scalar('mul', train_l, epoch)

老师的图

我的图···

线性回归的快速实现

import random
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import torch
from torch import nn,optim
import torch.nn.functional as F
from torch.utils.data import Dataset,TensorDataset,DataLoader
from torch.utils.tensorboard import SummaryWriter
from torchLearning import *

batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
num_epochs = 3

# 设置随机数种子
torch.manual_seed(420)

# 创建数据集
features, labels = tensorGenReg()
features = features[:, :-1]                                  # 剔除最后全是1的列
data = TensorDataset(features, labels)                       # 数据封装
batchData = DataLoader(data, batch_size = batch_size, shuffle = True)      # 数据加载


class LR(nn.Module):
    def __init__(self, in_features=2, out_features=1):  # 定义模型的点线结构
        super(LR, self).__init__()
        self.linear = nn.Linear(in_features, out_features)

    def forward(self, x):  # 定义模型的正向传播规则
        out = self.linear(x)
        return out

# 实例化模型
LR_model = LR()
#Stage 2.定义损失函数
criterion = nn.MSELoss()
#- Stage 3.定义优化方法
optimizer = optim.SGD(LR_model.parameters(), lr = 0.03)
#- Stage 4.模型训练

writer = SummaryWriter(log_dir='reg_loss')
def fit(net, criterion, optimizer, batchdata, epochs):
    for epoch in range(epochs):
        for X, y in batchdata:
            yhat = net.forward(X)
            loss = criterion(yhat, y)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
        print('epoch %d, loss %f' % (epoch + 1, loss))
        writer.add_scalar('loss', loss, global_step=epoch)

torch.manual_seed(420)
fit(net = LR_model,
    criterion = criterion,
    optimizer = optimizer,
    batchdata = batchData,
    epochs = num_epochs)

2、逻辑回归建模实验

手动实现逻辑回归

import random
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import torch
from torch import nn,optim
import torch.nn.functional as F
from torch.utils.data import Dataset,TensorDataset,DataLoader
from torch.utils.tensorboard import SummaryWriter
from torchLearning import *

#生成随机种子
torch.manual_seed(420)
#创建数据集
features, labels = tensorGenCla(num_class=2, bias=True)

#可视化展示
plt.scatter(features[:,0], features[:, 1], c=labels)
plt.show()

#激活函数
def sigmoid(z):
    return 1/(1+torch.exp(-z))

#逻辑回归模型
def logistic(X,w):
    return sigmoid(torch.mm(X, w))

#辅助函数
def cal(sigma, p=0.5):
    return((sigma >= p).float())

def accuracy(sigma, y):
    acc_bool = cal(sigma).flatten() == y.flatten()
    acc = torch.mean(acc_bool.float())
    return(acc)

def cross_entropy(sigma, y):
    return(-(1/y.numel())*torch.sum((1-y)*torch.log(1-sigma)+y*torch.log(sigma)))

#定义优化方法
def sgd(params, lr):
    params.data -= lr * params.grad
    params.grad.zero_()

#- Stage 4.训练模型
# 设置随机数种子
torch.manual_seed(420)

# 初始化核心参数
batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
num_epochs = 3                                 # 训练过程遍历几次数据
w = torch.ones(3, 1, requires_grad = True)     # 随机设置初始权重

# 参与训练的模型方程
net = logistic                                 # 使用逻辑回归方程
loss = cross_entropy                           # 交叉熵损失函数

# 训练过程
for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w), y)
        l.backward()
        sgd(w, lr)
    train_acc = accuracy(net(features, w), labels)
    print('epoch %d, accuracy %f' % (epoch + 1, train_acc))

快速实现逻辑回归

import random
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import torch
from torch import nn,optim
import torch.nn.functional as F
from torch.utils.data import Dataset,TensorDataset,DataLoader
from torch.utils.tensorboard import SummaryWriter
from torchLearning import *

batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
num_epochs = 3

torch.manual_seed(420)
# 创建数据集
features, labels = tensorGenCla(num_class=2)
features = features[:, :-1]
labels = labels.float()                                 # 损失函数要求标签也必须是浮点型
data = TensorDataset(features, labels)
batchData = DataLoader(data, batch_size = batch_size, shuffle = True)
#print(features)

class logisticR(nn.Module):
    def __init__(self, in_features=2, out_features=1):  # 定义模型的点线结构
        super(logisticR, self).__init__()
        self.linear = nn.Linear(in_features, out_features)

    def forward(self, x):  # 定义模型的正向传播规则
        out = self.linear(x)
        return out


# 实例化模型和
logic_model = logisticR()

#Stage 2.定义损失函数
criterion = nn.BCEWithLogitsLoss()
#Stage 3.定义优化方法
optimizer = optim.SGD(logic_model.parameters(), lr = lr)
#- Stage 4.模型训练
def fit(net, criterion, optimizer, batchdata, epochs):
    for epoch in range(epochs):
        for X, y in batchdata:
            zhat = net.forward(X)
            loss = criterion(zhat, y)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

# 设置随机数种子
torch.manual_seed(420)

fit(net = logic_model,
    criterion = criterion,
    optimizer = optimizer,
    batchdata = batchData,
    epochs = num_epochs)


def sigmoid(z):
    return 1/(1+torch.exp(-z))

#逻辑回归模型
def logistic(X,w):
    return sigmoid(torch.mm(X, w))

#辅助函数
def cal(sigma, p=0.5):
    return((sigma >= p).float())

def accuracy(sigma, y):
    acc_bool = cal(sigma).flatten() == y.flatten()
    acc = torch.mean(acc_bool.float())
    return(acc)

def acc_zhat(zhat, y):
    """输入为线性方程计算结果，输出为逻辑回归准确率的函数

    :param zhat：线性方程输出结果
    :param y: 数据集标签张量
    :return：准确率
    """
    sigma = sigmoid(zhat)
    return accuracy(sigma, y)

# 初始化核心参数
num_epochs = 20
LR1 = logisticR()
cr1 = nn.BCEWithLogitsLoss()
op1 = optim.SGD(LR1.parameters(), lr = lr)

# 创建列表容器
train_acc = []

# 执行建模
for epochs in range(num_epochs):
    fit(net = LR1,
        criterion = cr1,
        optimizer = op1,
        batchdata = batchData,
        epochs = epochs)
    epoch_acc = acc_zhat(LR1(features), labels)
    train_acc.append(epoch_acc)

# 绘制图像查看准确率变化情况
plt.plot(list(range(num_epochs)), train_acc)
plt.show()

3、softmax回归建模实验

手动实现

# 自定义模块
from torchLearning import *

from matplotlib import pyplot

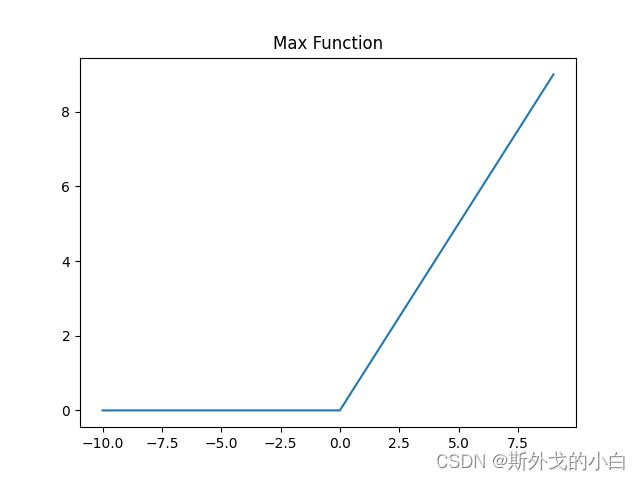
def max_x(x, delta=0.):
    x = np.array(x)
    negative_idx = x < delta
    x[negative_idx] = 0.
    return x
x = np.array(range(-10, 10))
s_j = np.array(x)

hinge_loss = max_x(s_j, delta=1.)

pyplot.plot(s_j, hinge_loss)
pyplot.title("Max Function")
pyplot.show()

def cross_entropy_test(s_k, s_j):
    soft_max = 1/(1+np.exp(s_k - s_j))
    cross_entropy_loss = -np.log(soft_max)
    return cross_entropy_loss
s_i = 0
s_k = np.array(range(-10, 10))

soft_x = cross_entropy_test(s_k, s_i)

pyplot.plot(x, hinge_loss)
pyplot.plot(range(-10, 10), soft_x)
pyplot.title("softmax vs Max")
pyplot.show()

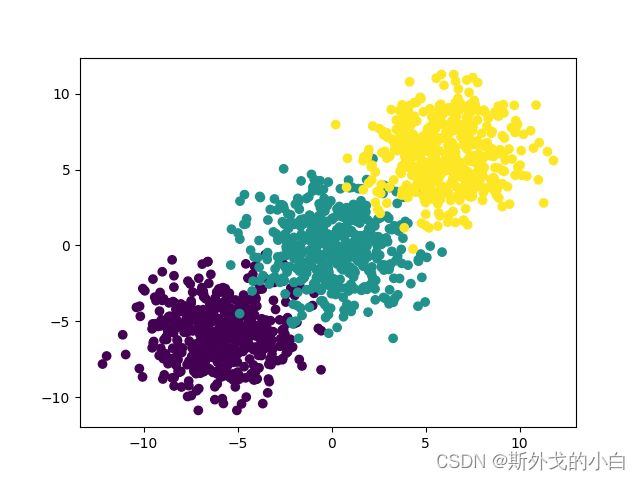
#1.生成数据集
# 设置随机数种子
torch.manual_seed(420)

features, labels = tensorGenCla(bias=True, deg_dispersion=[6, 2])
plt.scatter(features[:, 0], features[:, 1], c = labels)
plt.show()

def softmax(X, w):
    m = torch.exp(torch.mm(X, w))
    sp = torch.sum(m, 1).reshape(-1, 1)
    return m / sp

def m_cross_entropy(soft_z, y):
    y = y.long()
    prob_real = torch.gather(soft_z, 1, y)
    return (-(1/y.numel()) * torch.log(prob_real).sum())

def m_accuracy(soft_z, y):
    acc_bool = torch.argmax(soft_z, 1).flatten() == y.flatten()
    acc = torch.mean(acc_bool.float())
    return(acc)

def sgd(params, lr):
    params.data -= lr * params.grad
    params.grad.zero_()

# 设置随机数种子
torch.manual_seed(420)

# 数值创建
features, labels = tensorGenCla(bias = True, deg_dispersion = [6, 2])
plt.scatter(features[:, 0], features[:, 1], c = labels)
#plt.show()

# 设置随机数种子
torch.manual_seed(420)

# 初始化核心参数
batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
num_epochs = 3                                 # 训练过程遍历几次数据
w = torch.randn(3, 3, requires_grad = True)    # 随机设置初始权重

# 参与训练的模型方程
net = softmax                                     # 使用回归方程
loss = m_cross_entropy                            # 交叉熵损失函数

train_acc = []

# 模型训练过程
for epoch in range(num_epochs):
    for X, y in data_iter(batch_size, features, labels):
        l = loss(net(X, w), y)
        l.backward()
        sgd(w, lr)
    train_acc = m_accuracy(net(features, w), labels)
    print('epoch %d, acc %f' % (epoch + 1, train_acc))

快速实现

# 设置随机数种子
torch.manual_seed(420)

batch_size = 10                                # 每一个小批的数量
lr = 0.03                                      # 学习率
num_epochs = 3
# 创建数据集
features, labels = tensorGenCla(deg_dispersion = [6, 2])
labels = labels.float()    # 损失函数要求标签也必须是浮点型
features = features[:, :-1]
data = TensorDataset(features, labels)
batchData = DataLoader(data, batch_size = batch_size, shuffle = True)
#print(features)

class softmaxR(nn.Module):
    def __init__(self, in_features=2, out_features=3, bias=False):  # 定义模型的点线结构
        super(softmaxR, self).__init__()
        self.linear = nn.Linear(in_features, out_features)

    def forward(self, x):  # 定义模型的正向传播规则
        out = self.linear(x)
        return out


# 实例化模型和
softmax_model = softmaxR()
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(softmax_model.parameters(), lr = lr)
def fit(net, criterion, optimizer, batchdata, epochs):
    for epoch in range(epochs):
        for X, y in batchdata:
            zhat = net.forward(X)
            y = y.flatten().long()       # 损失函数计算要求转化为整数
            loss = criterion(zhat, y)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

fit(net = softmax_model,
    criterion = criterion,
    optimizer = optimizer,
    batchdata = batchData,
    epochs = num_epochs)

#print(softmax_model)

# 设置随机数种子
torch.manual_seed(420)

def m_accuracy(soft_z, y):
    acc_bool = torch.argmax(soft_z, 1).flatten() == y.flatten()
    acc = torch.mean(acc_bool.float())
    return(acc)

# 初始化核心参数
num_epochs = 20
SF1 = softmaxR()
cr1 = nn.CrossEntropyLoss()
op1 = optim.SGD(SF1.parameters(), lr = lr)

# 创建列表容器
train_acc = []

# 执行建模
for epochs in range(num_epochs):
    fit(net = SF1,
        criterion = cr1,
        optimizer = op1,
        batchdata = batchData,
        epochs = epochs)
    epoch_acc = m_accuracy(F.softmax(SF1(features), 1), labels)
    train_acc.append(epoch_acc)

# 绘制图像查看准确率变化情况
plt.plot(list(range(num_epochs)), train_acc)
plt.show()