李宏毅机器学习笔记06-卷积神经网络
为什么用CNN
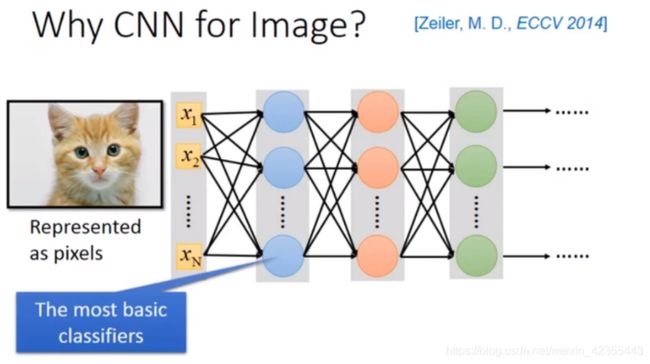
我们都知道CNN常常被用在影像处理上,如果你今天用CNN来做影像处理,当然也可以用一般的neural network来做影像处理,不一定要用CNN。比如说你想要做影像的分类,那么你就是training一个neural network,input一张图片,那么你就把这张图片表示成里面的pixel,也就是很长很长的vector。output就是(假如你有1000个类别,output就是1000个dimension)dimension。那我相信根据刚才那堂课内容,若给你一组training data你都可以描作出来。

但是呢,我们现在会遇到的问题是这样的,实际上我们在training neural network时,我们会期待说:在network的structure里面,每一个neural就是代表了一个最基本的classifier,事实在文件上根据训练的结果,你有可能会得到很多这样的结论。举例来说:第一层的neural是最简单的classifier,它做的事情就是detain有没有绿色出现,有没有黄色出现,有没有斜的条纹。
第二个layer是做比这个更复杂的东西,根据第一个layer的output,它看到直线横线就是窗框的一部分,看到棕色纹就是木纹,看到斜条纹+灰色可能是很多的东西(轮胎的一部分等等)
再根据第二个hidden layer的outpost,第三个hidden layer会做更加复杂的事情。
但现在的问题是这样的,当我们一般直接用fully connect feedforward network来做影像处理的时候,往往我们会需要太多的参数,举例来说,假设这是一张100 *100的彩色图(一张很小的imgage),你把这个拉成一个vector,(它有多少个pixel),它有100 *100 3的pixel。
如果是彩色图的话,每个pixel需要三个value来描述它,就是30000维(30000 dimension),那input vector假如是30000dimension,那这个hidden layer假设是1000个neural,那么这个hidden layer的参数就是有30000 *1000,那这样就太多了。那么CNN做的事就是简化neural network的架构。我们把这里面一些根据人的知识,我们根据我们对影像就知道,某些weight用不上的,我们一开始就把它滤掉。不是用fully connect feedforward network,而是用比较少的参数来做影像处理这件事。所以CNN比一般的DNN还要简单的。
等一下我们讲完会觉得发现说:你可能觉得CNN运作很复杂,但事实上它的模型是要比DNN还要更简单的。我们就是用power-knowledge 去把原来fully connect layer中一些参数拿掉就成了CNN。
Small region
我们先来讲一下,为什么我们有可能把一些参数拿掉(为什么可以用比较少的参数可以来做影像处理这件事情)
这里有几个观察,第一个是在影像处理里面,我们说第一层的 hidden layer那些neural要做的事就是侦测某一种pattern,有没有某一种patter出现。大部分的pattern其实要比整张的image还要小,对一个neural来说,假设它要知道一个image里面有没有某一个pattern出现,它其实是不需要看整张image,它只要看image的一小部分。
举例来说,假设我们现在有一张图片,第一个hidden layer的某一种neural的工作就是要侦测有没有鸟嘴的存在(有一些neural侦测有没有爪子的存在,有没有一些neural侦测有没有翅膀的存在,有没有尾巴的存在,合起来就可以侦测图片中某一只鸟)。假设有一个neural的工作是要侦测有没有鸟嘴的存在,那并不需要看整张图,其实我们只需要给neural看着一小红色方框的区域(鸟嘴),它其实就可以知道说,它是不是一个鸟嘴。对人来说也是一样,看这一小块区域这是鸟嘴,不需要去看整张图才知道这件事情。所以,每一个neural连接到每一个小块的区域就好了,不需要连接到整张完整的图。
Same Patterns
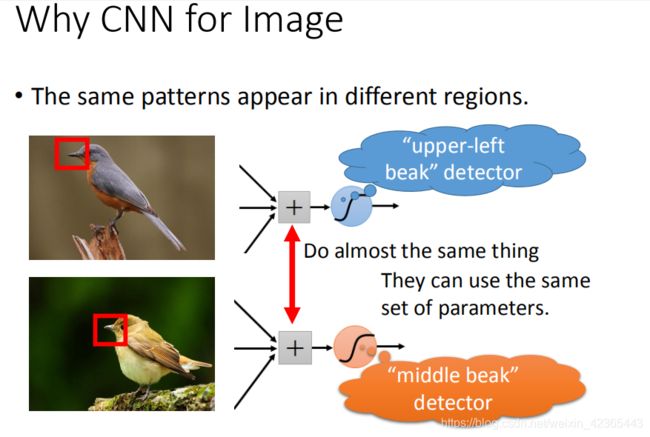
第二个观察是这样子,同样的pattern在image里面,可能会出现在image不同的部分,但是代表的是同样的含义,它们有同样的形状,可以用同样的neural,同样的参数就可以把patter侦测出来。
比如说,这张图里面有一张在左上角的鸟嘴,在这张图里面有一个在中央的鸟嘴,但是你并不需要说:我们不需要去训练两个不同的detector,一个专门去侦测左上角的鸟嘴,一个去侦测中央有没有鸟嘴。如果这样做的话,这样就太冗了。我们不需要太多的冗源,这个nerual侦测左上角的鸟嘴跟侦测中央有没有鸟嘴做的事情是一样的。我们并不需要两个neural去做两组参数,我们就要求这两个neural用同一组参数,就样就可以减少你需要参数的量
Subsampling
第三个是:我们知道一个image你可以做subsampling,你把一个image的奇数行,偶数列的pixel拿掉,变成原来十分之一的大小,它其实不会影响人对这张image的理解。对你来说:这张image跟这张image看起来可能没有太大的差别。是没有太大的影响的,所以我们就可以用这样的概念把image变小,这样就可以减少你需要的参数。
CNN架构
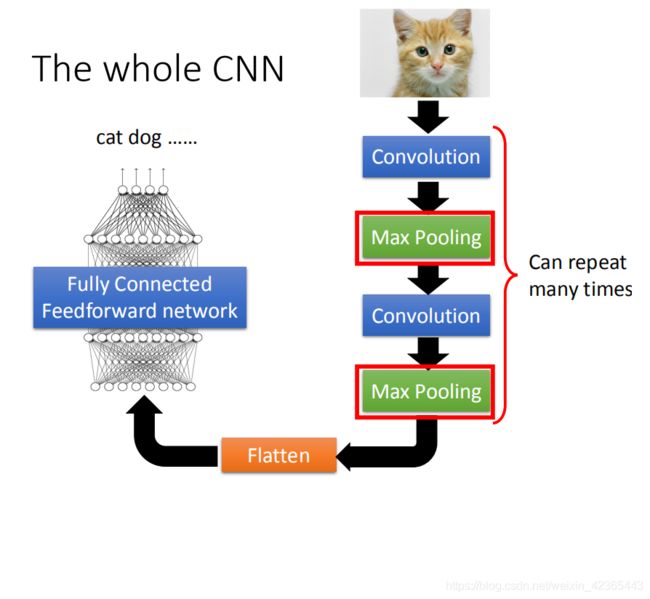
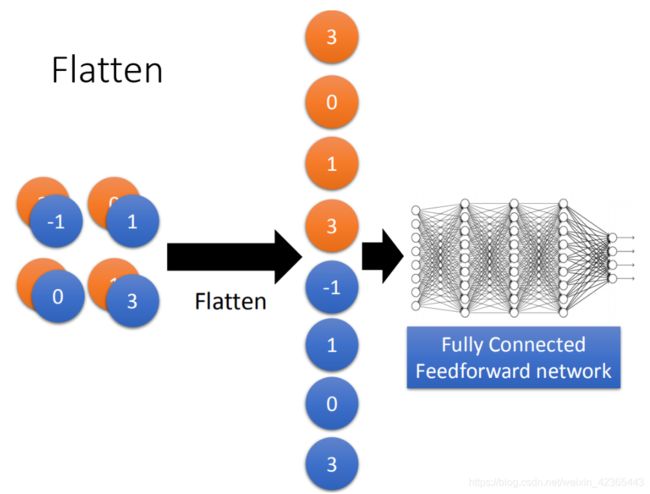
所以整个CNN的架构是这样的,首先input一张image以后,这张image会通过convolution layer,接下里做max pooling这件事,然后在做convolution,再做max pooling这件事。这个process可以反复无数次,反复的次数你觉得够多之后,(但是反复多少次你是要事先决定的,它就是network的架构(就像你的neural有几层一样),你要做几层的convolution,做几层的Max Pooling,你再定neural架构的时候,你要事先决定好)。你做完决定要做的convolution和Max Pooling以后,你要做另外一件事,这件事情叫做flatten,再把flatten的output丢到一般fully connected feedforward network,然后得到影像辨识的结果。

我们刚才讲基于三个对影像处理的观察,所以设计了CNN这样的架构。
第一个观察是,要生成一个pattern,不要看整张的image,你只需要看image的一小部分。第二是,通用的pattern会出现在一张图片的不同的区域。第三个是,我们可以做subsampling
前面的两个property可以用convolution来处理掉,最后的property可以用Max Pooling这件事来处理。等一下我们要介绍每一个layer再做的事情,我们就先从convolution开始看起。
Convolution
Propetry1
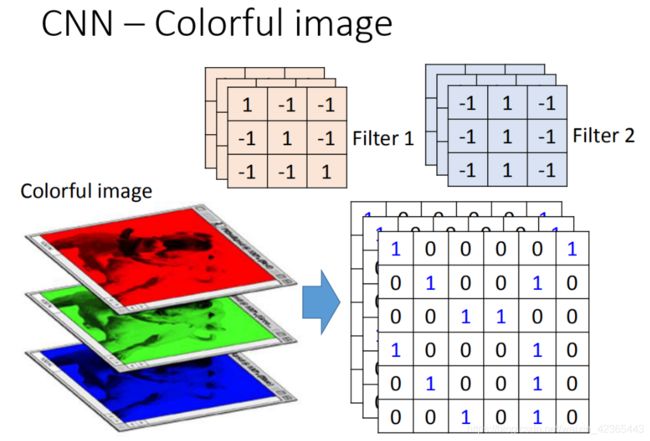
假设现在我们的network的input是一张6*6的Image,如果是黑白的,一个pixel就只需要用一个value去描述它,1就代表有涂墨水,0就代表没有涂到墨水。那在convolution layer里面,它由一组的filter,(其中每一个filter其实就等同于是fully connect layer里面的一个neuron),每一个filter其实就是一个matrix(3 *3),这每个filter里面的参数(matrix里面每一个element值)就是network的parameter(这些parameter是要学习出来的,并不是需要人去设计的)
每个filter如果是3* 3的detects意味着它就是再侦测一个3 *3的pattern(看3 *3的一个范围)。在侦测pattern的时候不看整张image,只看一个3 *3的范围内就可以决定有没有某一个pattern的出现。这个就是我们考虑的第一个Property
Propetry2
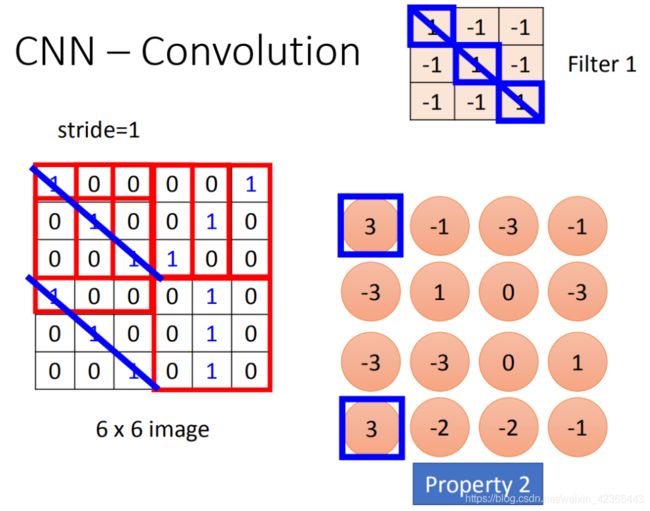
这个filter咋样跟这个image运作呢?首先第一个filter是一个3* 3的matrix,把这个filter放在image的左上角,把filter的9个值和image的9个值做内积,两边都是1,1,1(斜对角),内积的结果就得到3。(移动多少是事先决定的),移动的距离叫做stride(stride等于多少,自己来设计),内积等于-1。stride等于2,内积等于-3。我们先设stride等于1。
你把filter往右移动一格得到-1,再往右移一格得到-3,再往右移动一格得到-1。接下里往下移动一格,得到-3。以此类推(每次都移动一格),直到你把filter移到右下角的时候,得到-1(得到的值如图所示)
经过这件事情以后,本来是6 *6的matrix,经过convolution process就得到4 *4的matrix。如果你看filter的值,斜对角的值是1,1,1。所以它的工作就是detain1有没有1,1,1(连续左上到右下的出现在这个image里面)。比如说:出现在这里(如图所示蓝色的直线),所以这个filter就会告诉你:左上跟左下出现最大的值
就代表说这个filter要侦测的pattern,出现在这张image的左上角和左下角,这件事情就考虑了propetry2。同一个pattern出现在了左上角的位置跟左下角的位置,我们就可以用filter 1侦测出来,并不需要不同的filter来做这件事。
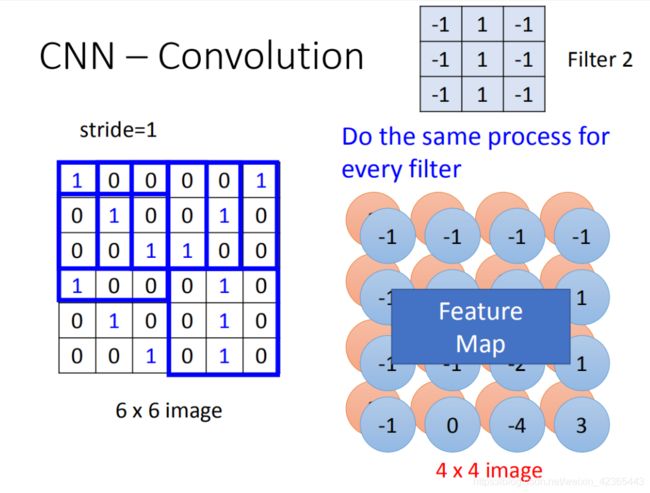
在一个convolution layer 里面会有很多的filter(刚才只是一个filter的结果),那另外的filter会有不同的参数(图中显示的filter2),它也做跟filter1一模一样的事情,在filter放到左上角再内积得到结果-1,依次类推。你把filter2跟 input image做完convolution之后,你就得到了另一个4*4的matrix,红色4 *4的matrix跟蓝色的matrix合起来就叫做feature map,看你有几个filter,你就得到多少个image(你有100个filter,你就得到100个4 *4的image)
刚才举的例子是一张黑白的image,所以input是一个matrix。若今天换成彩色的image,彩色的image是由RGB组成的,所以,一个彩色的image就是好几个matrix叠在一起,就是一个立方体。如果要处理彩色image,这时候filter不是一个matrix,filter而是一个立方体。如果今天是RGB表示一个pixel的话,那input就是3*6 *6,那filter就是3 *3 *3。
在做convolution的话,就是将filter的9个值和image的9个值做内积(不是把每一个channel分开来算,而是合在一起来算,一个filter就考虑了不同颜色所代表的channel)
convolution和fully connected之间的关系
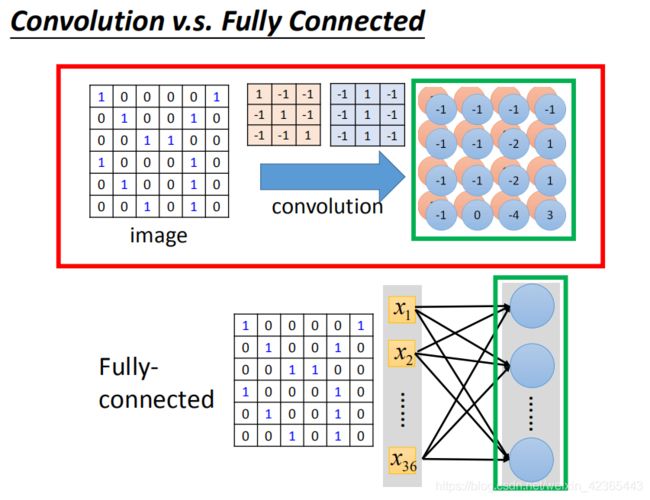
convolution就是fully connected layer把一些weight拿掉了。经过convolution的output其实就是一个hidden layer的neural的output。如果把这两个link在一起的话,convolution就是fully connected拿掉一些weight的结果。
我们在做convolution的时候,我们filter1放到左上角(先考虑filter1),然后做inner product,得到内积为3,这件事情就等同于把6* 6的image拉直(变成如图所示)。然后你有一个neural的output是3,这个neural的output考虑了9个pixel,这9个pixel分别就是编号(1,2,3,7,8,9,13,14,15)的pixel。这个filter做inner product以后的output 3就是某个neuron output 3时,就代表这个neuron的weight只连接到(1,2,3,7,8,9,13,14,15)。这9个weight就是filter matrix里面的9个weight(同样的颜色)
在fully connected中,一个neural应该是连接在所有的input(有36个pixel当做input,这个neuron应连接在36个input上),但是现在只连接了9个input(detain一个pattern,不需要看整张image,看9个input就好),这样做就是用了比较少的参数了。

将stride=1(移动一格)做内积得到另外一个值-1,假设这个-1是另外一个neural的output,这个neural连接到input的(2,3,4,8,9,10,14,15,16),同样的weight代表同样的颜色。在9个matrix
当我们做这件事情就意味说:这两个neuron本来就在fully connect里面这两个neural本来是有自己的weight,当我们在做convolution时,首先把每一个neural连接的wight减少,强迫这两个neural共用一个weight。这件事就叫做shared weight,当我们做这件事情的时候,我们用的这个参数就比原来的更少。
Max pooling
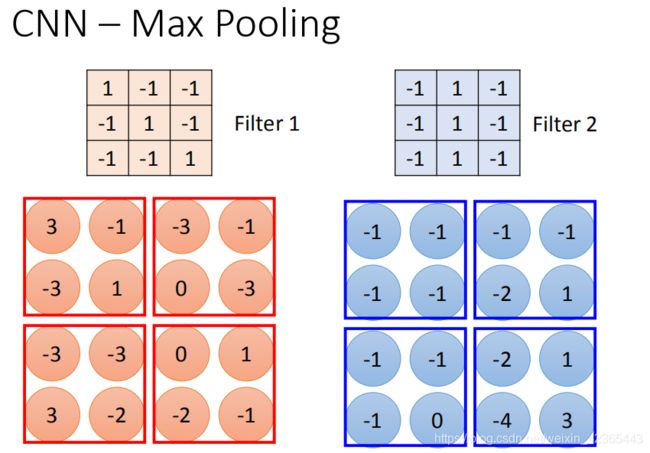
相对于convolution来说,Max Pooling是比较简单的。我们根据filter 1得到4*4的maxtrix,根据filter2得到另一个4 *4的matrix,接下来把output ,4个一组。每一组里面可以选择它们的平均或者选最大的都可以,就是把四个value合成一个value。这个可以让你的image缩小。
假设我们选择四个里面的max vlaue保留下来,这样可能会有个问题,把这个放到neuron里面,这样就不能够微分了,但是可以用微分的办法来处理的
做完一个convolution和一次max pooling,就将原来6 * 6的image变成了一个2 *2的image。这个2 *2的pixel的深度depend你有几个filter(你有50个filter你就有50维),得到结果就是一个new image but smaller,一个filter就代表了一个channel。
这件事可以repeat很多次,通过一个convolution + max pooling就得到新的 image。它是一个比较小的image,可以把这个小的image,做同样的事情,再次通过convolution + max pooling,将得到一个更小的image。
这边有一个问题:第一次有25个filter,得到25个feature map,第二个也是由25个filter,那将其做完是不是要得到$25^2$的feature map。其实不是这样的!
假设第一层filter有2个,第二层的filter在考虑这个imput时是会考虑深度的,并不是每个channel分开考虑,而是一次考虑所有的channel。所以convolution有多少个filter,output就有多少个filter(convolution有25个filter,output就有25个filter。只不过,这25个filter都是一个立方体)
Flatten
flatten就是feature map拉直,拉直之后就可以丢到fully connected feedforward netwwork,然后就结束了。
CNN in Keras
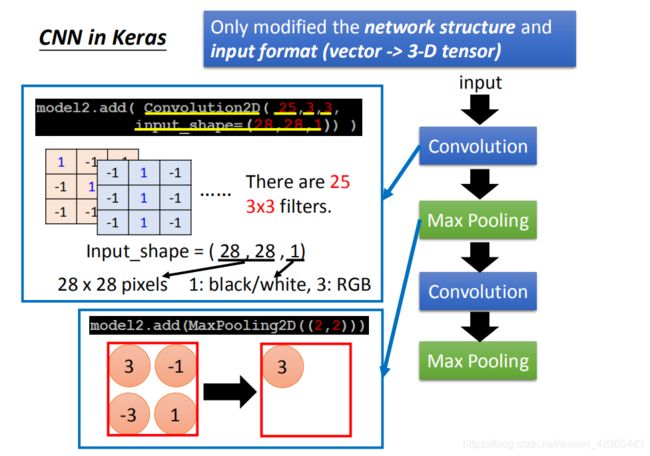
唯一要改的是:network structure和input format,本来在DNN中input是一个vector,现在是CNN的话,会考虑 input image的几何空间的,所以不能给它一个vector。应该input一个tensor(高维的vector)。为什么要给三维的vector?因为image的长宽高各是一维,若是彩色的话就是第三维。所以要给三维的tensor
model.add(Convolution2D( 25, 3, 3)
25代表有25个filter,3 *3代表filter是一个3 *3的matrix
Input_shape=(28,28,1)
假设我要做手写数字辨识,input是28 *28的image,每个pixel都是单一颜色。所以input_shape是(1,28,28)。如果是黑白图为1(blacj/white),如果是彩色的图时为3(每个pixel用三个值来表述)。
MaxPooling2D(( 2, 2 ))
2,2表示把2*2的feature map里面的pixel拿出来,选择max value

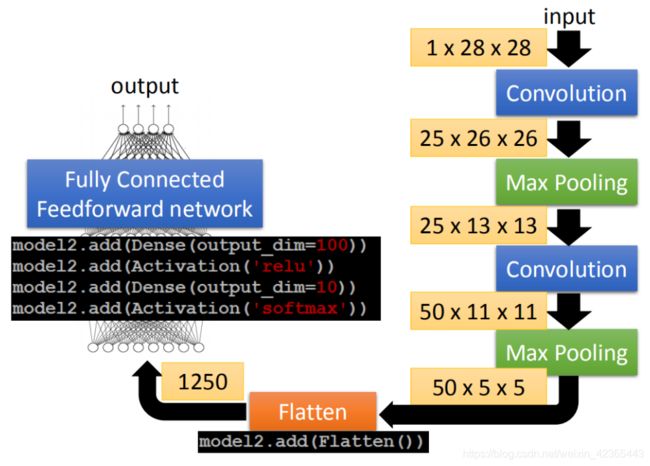
假设我们input一个1 *28 * 28的image,你就可以写model.add(Convolution2D( 25, 3, 3, Input_shape=(28,28,1)))。通过convplution以后得到output是25 *26 26(25个filter,通过3 *3得到26 * 26)。然后做max pooling,2 *2一组选择 max value得到 25 *13 * 13
然后在做一次convolution,假设我在这选50个filter,每一个filter是3 *3时,那么现在的channel就是50。13 *13的image通过3 *3的filter,就成11 *11,然后通过2 *2的Max Pooling,变成了50 *5 *5
在第一个convolution layer里面,每一个filter有9个参数,在第二个convolution layer里面,虽然每一个filter都是3 *3,但不是3 *3个参数,因为它input channel 是25个,所以它的参数是3 *3 *25(225)。
通过两次convolution,两次Max Pooling,原来是1 *28 *28变为50 *5 *5。flatten的目的就是把50 *5 *5拉直,拉直之后就成了1250维的vector,然后把1250维的vector丢到fully connected。
CNN学到了什么?
很多人常会说:deep learning就是一个黑盒子,然后你learn以后你不知道它得到了什么,所以有很多人不喜欢用这种方法。但还有很多的方法分析的,比如说我们今天来示范一下咋样分析CNN,它到底学到了什么。
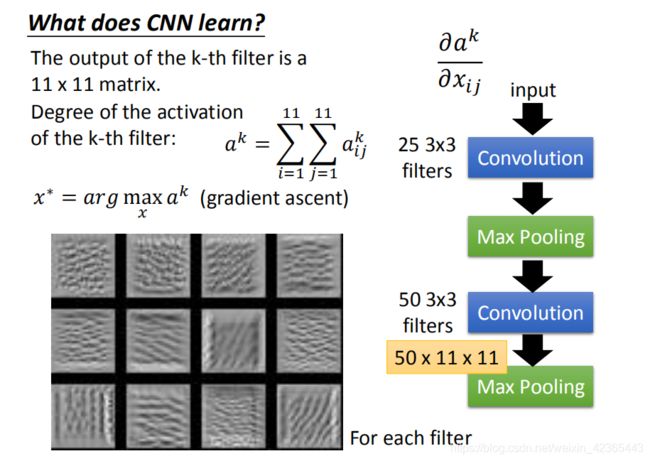
分析input第一个filter是比较容易的,因为一个layer每一个filter就是一个3*3的mmatrix,对应到3 *3的范围内的9个pixel。所以你只要看到这个filter的值就可以知道说:它在detain什么东西,所以第一层的filter是很容易理解的,但是你没有办法想要它在做什么事情的是第二层的filter。在第二层我们也是3 *3的filter有50个,但是这些filter的input并不是pixel(3 *3的9个input不是pixel)。而是做完convolution再做Max Pooling的结果。所以这个3 *3的filter就算你把它的weight拿出来,你也不知道它在做什么。另外这个3 *3的filter它考虑的范围并不是3 *3的pixel(9个pixel),而是比9个pxiel更大的范围。不要这3 *3的element的 input是做完convolution再加Max Pooling的结果。所以它实际上在image上看到的范围,是比3 *3还要更大的。那我们咋样来分析一个filter做的事情是什么呢,以下是一个方法。
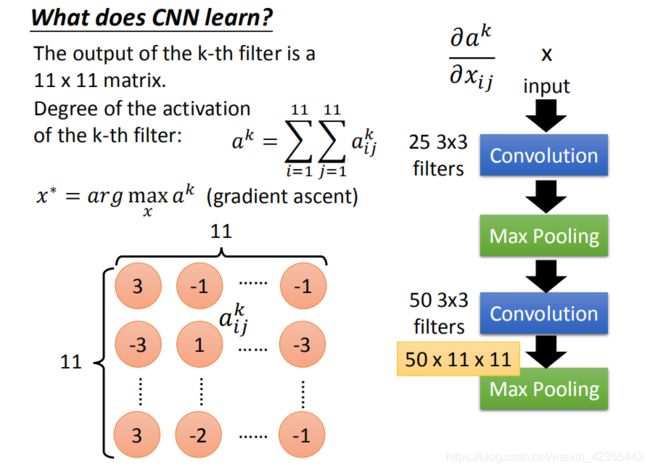
我们知道现在做第二个convolution layer里面的50个filter,每一个filter的output就是一个matrix(11*11的matrix)。假设我们现在把第k个filter拿出来,它可能是这样子的(如图),每一个element我们就叫做$a_{ij}^k$(上标是说这是第k个filter,i,j代表在这个matrix里面的第i row和第j column)。
接下来我们定义一个东西叫做:“Degree of the activation of the k-th filter”,我们定义一个值代表说:现在第k个filter有多被active(现在的input跟第k个filter有多match),第k个filter被启动的Degree定义成:这个11*11的 matrix里面全部的 element的summation。(input一张image,然后看这个filter output的这个11 *11的值全部加起来,当做是这个filter被active的程度)
截下来我们要做的事情是这样子的:我们想知道第k个filter的作用是什么,所以我们想要找一张image,这张image它可以让第k个filter被active的程度最大。
假设input一张image,我们称之为X,那我们现在要解的问题就是:找一个x,它可以让我们现在定义的activation Degree $a^k$最大,这件事情要咋样做到呢?其实是用gradient ascent你就可以做到这件事(minimize使用gradient descent,maximize使用gradient ascent)
这是事还是蛮神妙的,我们现在是把X当做我们要找的参数用gradient ascent做update,原来在train CNN network neural的时候,input是固定的,model的参数是你需要用gradient descent找出来的,用gradient descent找参数可以让loss被 minimize。但是现在立场是反过来的,现在在这个task里面,model的参数是固定的,我们要让gradient descent 去update这个X,可以让这个activation function的Degree of the activation是最大的。
这个是得到的结果,如果我们随便取12个filter出来,每一个filter都去找一张image,这个image可以让那个filter的activation最大。现在有50个filter,你就要去找50张image,它可以让这些filter的activation最大。我就随便取了前12个filter,可以让它最active的image出来(如图)。
这些image有一个共同的特征就是:某种纹路在图上不断的反复。比如说第三张image,上面是有小小的斜条纹,意味着第三个filter的工作就是detain图上有没有斜的条纹。那不要忘了每一个filter考虑的范围都只是图上一个小小的范围。所以今天一个图上如果出现小小的斜的条纹的话,这个filter就会被active,这个output的值就会比较大。那今天如果让图上所有的范围通通都出现这个小小的斜条纹的话,那这个时候它的Degree activation会是最大的。(因为它的工作就是侦测有没有斜的条纹,所以你给它一个完整的数字的时候,它不会最兴奋。你给它都是斜的条纹的时候,它是最兴奋的)
所以你就会发现:每一个filter的工作就是detain某一张pattern。比如说:第三图detain斜的线条,第四图是detain短的直线条,等等。每一个filter所做的事情就是detain不同角度的线条,如果今天input有不同角度的线条,你就会让某一个activation function,某一个filter的output值最大
分析全连接层
在做完convolution和Max Pooling以后,要做一件事情叫做flatten,把flatten的结果丢到neural network里面去。那我们想要知道:在这个neural network里面,每一个neural的工作是什么。
我们要做的事情是这样的:定义第j个neural,它的output叫做$a_j$。接下来我们要做事情就是:找一张image(用gradient ascent的方法找一张X),这个image X你把它丢到neural network里面去,它可以让$a_j$的值被maximize。找到的结果就是这样的(如图)
如图是随便取前9个neural出来,什么样的图丢到CNN里面可以让这9个neural最被active output的值最大,就是这9张图(如图)
这些图跟刚才所观察到图不太一样,在刚在的filter观察到的是类似纹路的图案,在整张图上反复这样的纹路,那是因为每个filter考虑是图上一个小小的range(图上一部分range)。现在每一个neural,在你做flatten以后,每个neural的工作就是去看整张图,而不是是去看图的一小部分。
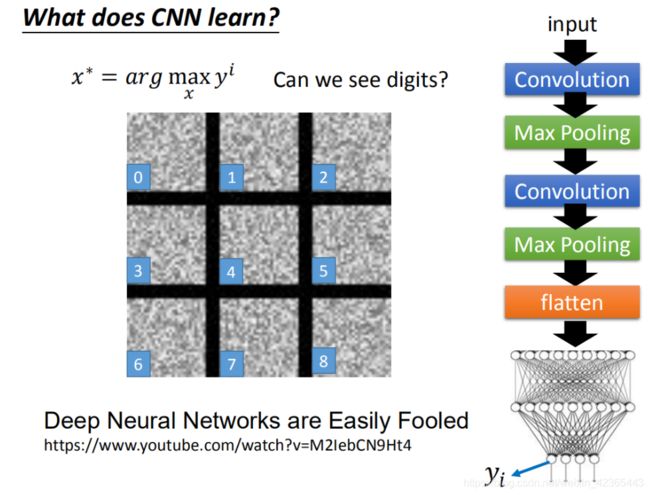
那今天我们考虑是output呢?(output就是10维,每一维对应一个digit)我们把某一维拿出来,找一张image让那个维度output最大。那我们会得到咋样的image呢?你可以想象说:每一个output,每一个dimension对应到某一个数字。
现在我们找一张image,它可以让对应在数字1的output 最大,那么那张image显然就像看起来是数字1。你可以期待说:我们可以用这个方法让machine自动画出数字。
但是实际上我们得到的结果是这样子的,每一张图分别代表数字0-9。也就是说:我们到output layer对应到0那个neuron,其实是这样的(如图),以此类推。你可能会有疑惑,为什么是这样子的,是不是程序有bug。为了确定程序没有bug,再做了一个实验是:我把每张image(如图)都丢到CNN里面,然后看它classifier的结果是什么。CNN确定就说:这个是1,这个是,…,这个是8。CNN就觉得说:你若拿这张image train出来正确率有98的话,就说:这个就是8。所以就很神奇
这个结果在很多的地方有已经被观察到了,今天的这个neuron network它所学到东西跟我们人类是不太一样的(它所学到的东西跟我们人类想象和认知不一样的)。你可以查看这个链接的paper(如图)
相关的paper
让图更像数字
我们有没有办法让这个图看起来更像数字呢?想法是这样的:一张图是不是数字我们有一些基本的假设,比如说:这些就算你不知道它是什么数字(显然它不是digit),人类手写出来的就不是这个样子。所以我们应该对x做constraint,我们告诉machine,有些x可能会使y很大但不是数字。我们根据人的power-knowledge就知道,这些x不可能是一些数字。那么我们可以加上咋样的constraint呢?(图中白色的亮点代表的是有墨水的,对一个digit来说,图白的部分其实是有限的,对于一个数字来说,一整张图的某一个小部分会有笔画,所以我们应该对这个x做一些限制)
假设image里面的每一个pixel用$x_{ij}$来表示,(每一个image有28 *28的pixel)我们把所有image上$i,j$的值取绝对值后加起来。如果你熟悉machine learning的话,这一项就是L1-regularization。然后我们希望说:在找一个x可以让$y^i$最大的同时让$|x_{ij}|$的summation越小越好。也就是我们希望找出的image,大部分的地方是没有涂颜色的,只有非常少的部分是有涂颜色的。如果我们加上constraint以后我们得到的结果是这样的(如右图所示),跟左边的图比起来,隐约可以看出来它是一个数字(得到的结果看起来像数字)
你可能会有一个问题,绝对值咋样去微分,下堂课会讲到
你如果加上一些额外的constraint,比如说:你希望相邻的pixel
是同样的颜色等等,你应该可以得到更好的结果。不过其实有更多很好的方法可以让machine generate数字
Deep Dream
其实上述的想法就是Deep Dream的精神,Deep Dream是说:如果你给machine一张image,它会在这张image里加上它看到的东西。咋样做这件事情呢?你先找一张image,然后将这张image丢到CNN中,把它的某一个hidden layer拿出来(vector),它是一个vector(假设这里是:[3.9, -1.5, 2.3…])。接下来把postitive dimension值调大,把negative dimension值调小(正的变的更正,负的变得更负)。你把这个(调节之后的vector)当做是新的image的目标(把3.9的值变大,把-1.5的值变得更负,2.3的值变得更大。然后找一张image(modify image)用GD方法,让它在hidden layer output是你设下的target)。这样做的话就是让CNN夸大化它所看到的东西,本来它已经看到某一个东西了,你让它看起来更像它原来看到的东西。本来看起来是有一点像东西,它让某一个filter有被active,但是你让它被active的更剧烈(夸大化看到的东西)。

如果你把这张image拿去做Deep Dream的话,你看到的结果是这样子的。右边有一只熊,这个熊原来是一个石头(对机器来说,这个石头有点像熊,它就会强化这件事情,所以它就真的变成了一只熊)。Deep Dream还有一个进阶的版本,叫做Deep Style
Deep style
今天input一张image,input一张image,让machine去修改这张图,让它有另外一张图的风格 (类似于风格迁移)
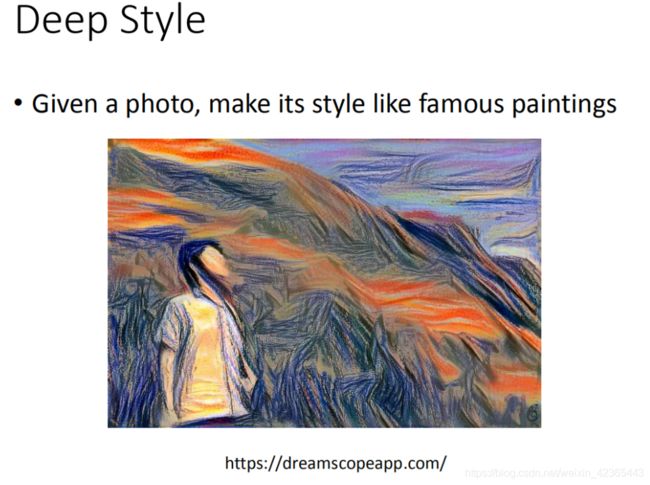
这里给一个reference给参考
其中做法的精神是这样的:原来的image丢给CNN,然后得到CNN的filter的output,CNN的filter的output代表这张image有什么content。接下来你把呐喊这张图也丢到CNN里面,也得到filter的output。我们并不在意一个filter ,而是在意filter和filter之间
的convolution,这个convolution代表了这张image的style。
接下来你用同一个CNN找一张image,这张image它的content像左边这张相片,但同时这张image的style像右边这张相片。你找一张image同时可以maximize左边的图,也可以maximize右边的图。那你得到的结果就是像最底下的这张图。用的就是刚才讲的gradient ascent的方法找一张image,然后maximize这两张图,得到就是底下的这张图。
CNN的应用
围棋
我们现在CNN已经在很多不同的应用上,而不是只有影像处理上。比如:CNN现在有一个很知名的应用,就用用在下围棋上面。为什么CNN可以用来下围棋上面呢?
我们知道如果让machine来下围棋,你不见得需要用CNN。其实一般的topic neuron network也可以帮我们做到这件事情。你只要learn一个network(也就是找一个function),它的input是棋盘,output是棋盘上的位置。也就是说:你根据这个棋盘的盘式,如果你下一步要落子的话,你落子的位置其实就可以让machine学会。
所以你用Fully-connected feedforward network也可以帮我们做到让machine下围棋这件事情。也就是你只要告诉input是一个19 *19的vector,每一个vector的dimension对应到棋盘上面的每一个位置。machine就可以学会下围棋了。
如果那个位置有一个黑子的话就是1,如果有一个白子的话就是-1,反之就是0。
但是我们这边采用CNN的话,我们会得到更好的performance。我们之前举的例子是把CNN用在影像上面,也就是input是matrix(也就是把19*19的vector表示成19 *19的matrix),然后当做一个image来看,然后让它output 下一步落子的位置就结束了。
告诉machine说:看到落子在“5之五”,CNN的output就是在“天元”的地方是1,其他地方是0。看到“5之五”和“天元”都有子,CNN的output就是在“五之5”的地方是1,其他地方是0。这个是supervised部分

现在大家都说“AlphaGo”,都是懂懂的样子。但是自从“AlphaGo”用了CNN以后,大家都觉得说:CNN应该很厉害。所以如果你没有用CNN来处理你的问题,别人就会问你为什么不用CNN来处理问题(比如说:面试的时候),CNN不是比较强吗
什么时候应该用CNN呢?image必须有该有的那些特性,在CNN开头就有说:根据那三个观察,所以设计出了CNN这样的架构。在处理image时是特别有效的。为什么这样的架构也同样可以用在围棋上面(因为围棋有一些特性跟影像处理是非常相似的)
第一个是:在image上面,有一些pattern是要比整张image还要小的多的(比如:鸟喙是要比整张的image要小的多),只需要看那一小的部分就知道那是不是鸟喙。在围棋上也有同样的现象,如图所示,一个白子被三个黑子围住(这就是一个pattern),你现在只需要看这一小小的范围,就可以知道白子是不是没“气”了,不需要看整个棋盘才能够知道这件事情,这跟image是有同样的性质。
在“AlphaGo”里面它的第一个layer filter其实就是用5*5的filter,显然做这个设计的人觉得说:围棋最基本的pattern可能都是在5 *5的范围内就可以被侦测出来,不需要看整个棋牌才能知道这件事情。
接下来我们说image还有一个特性:同样的pattern会出现在不同的regions,而他们代表的是同样的意义,在围棋上可能也会有同样的现象。像如图这个pattern可以出现在左上角,也可以出现在右下角,它们都代表了同样的意义。所以你可以用同一个pattern来处理在不同位置的同样的pattern。所以对围棋来说,是有这两个特性的。
AlphaGo
但是没有办法让我想通的地方就是第三点,我们可以对一个image做subsampling,把image变为原来的1/4的大小,但是也不会影响你看这张图的样子。因为基于这个观察,所以有Max Pooling这个layer。但是对围棋来说,你可以做这件事情吗?你可以丢到奇数行偶数类,这样它还是同一个盘式吗,显然不是的,这个让我相当的困扰。
“AlphaGo”里面有用了Max Pooling这个架构,或许这是一个弱点。可以针对这个弱点去攻击它,击败它。但是“AlphaGo”(比李世石还强),没有这个显而易见的弱点
有一天我突然领悟到“AlphaGo”的CNN架构里面有什么特别的地方(“AlphaGo”Paper的附录),在“AlphaGo”Paper里面只说了一句:用CNN架构,但它没有在正文里仔细描述CNN的架构,会不会实际上CNN架构里有什么特别的玄机呢?
在“AlphaGo”Paper的附录里面,描述了neuron network structure,它的input是一个19 *19 *48的image。19 *1是可以理解,因为棋盘就是19 *19。48是咋样来的呢?对于“AlphaGo”来说,它把每一个位置都用48个value来描述。这里面的value包括:我们只要在一个位置来描述有没有白子,有没有黑子;还加上了domain-knowledge(不只是说:有没有黑子或者白子,还会看这个位置是不是出于没“气”的状态,等等)
如果读完这段你会发现:第一个layer有做 zero pads。也就是说:把原来19*19的image外围补上更多的0,让它变成23 *23的image。
第一个hidden layer用的是5*5 filter(总共有k个filter),k的值在Paper中用的是192(k=192);stride设为1;使用RLU activation function等等。
然后你就会发现“AlphaGo”是没有用Max Pooling,所以这个neuron network的架构设计就是“运用之妙,存乎一心”。虽然在image里面我们都会用Max Pooling这个架构,但是针对围棋的特性来设计neuron network的时候,我们是不需要Max Pooling这个架构的,所以在“AlphaGo”里面没有这个架构.
语音
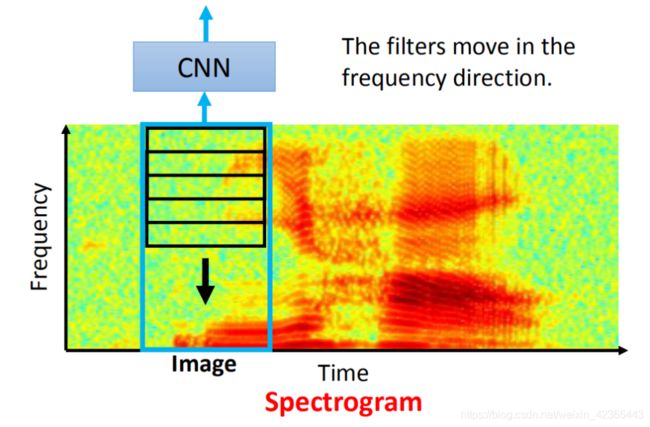
CNN也可以用在其它的task里面,比如说:CNN也用在影像处理上。如图是一段声音,你可以把一段声音表示成Spectrogram(横轴是时间,纵轴是那段时间里面声音的频率),红色代表:在那段时间里那一频率的energy比较大。
这张image其实是我说“你好”,然后看到的Spectrogram。有通过训练的人,看这张image,就知道这句话的内容是什么。
人既然可以看这个image就可以知道是什么样的声音讯号,那我们也可以让机器把这个Spectrogram当做一张image。然后用CNN来判断:input一张image,它是对应什么样的声音讯号(单位可能是phone)。但是神奇的地方是:CNN里面的时候,在语音上,我们通常只考虑在frequency方向上移动的filter。也就是说:我们的filter是长方形的,其中宽是跟image的宽是一样的,我们在移动filter的时候,我们移这个方向(如图所示)
如果把filter向时间的方向移动的话,结果是没有太大的帮助。这样的原因是:在语音里面,CNN的output还会接其他的东西(比如:LSTM),所以在向时间方向移动是没有太多的帮助。
为什么在频率上的filter会有帮助呢?我们用filter的目的是:为了detain同样的pattern出现在不同的range,我们都可以用同一个的filter detain出来。那在声音讯号上面,男生跟女生发同样的声音(同样说“你好”),Spectrogram看起来是非常不一样的,它们的不同可能只是频率的区别而已(男生的“你好”跟女生的“你好”,它们的pattern其实是一样的)
所以今天我们把filter在frequency direction移动是有效的。当我们把CNN用在application时,你永远要想一想,这个application的特性是什么,根据那个application的特性来design network的structure
文本
相关的paper
我们知道CNN耶可以用在文字处理上面,这个是从paper截下来的图。在文字处理上面,假设你要做的是:让machine侦测这个word sequence代表的是positive还是negative。首先input一个word sequence,你把word sequence里面的每一个word都用一个vector来表示。这边的每一个vector代表word本身的sementic,如果两个word含义越接近的话,那它们的vector在高维的空间上就越接近,这个就叫做“wordembedding”(每一个word用vector来表示)。
当你把每一个word用vector来表示的时候,你把sentence所有的word排在一起,它就变成一张image。你可以把CNN套用在这个image上面。
当我们把CNN用在文字处理上的时候,你的filter其实是这个样子的(如图所示)。它的高跟image是一样的,你把filter沿着句子里面词汇的顺序来移动,然后你就会得到一个vector。不同的filter就会得到不同的vector,然后Max Pooling,然后把Max Pooling的结果丢到fully connect里面,就会得到最后的结果。在文字处理上,filter只在时间的序列上移动,不会在“embedding dimension”这个方向上移动。如果你有做过类似的task(文字处理),知道“embedding dimension”指的是什么,你就会知道在“embedding dimension”反向上移动是没有帮助的,因为在word embedding里面每一个dimension的含义其实是独立的。所以当我们如果使用CNN的时候,你会假设说:第二个dimension跟第一个dimension有某种特别的关系;第四个dimension跟第五个dimension有某种特别的关系。这个关系是重复的(这个pattern出现在不同的位置是同样的意思)。但是在word embedding里面,不同dimension是独立的(independent)。所以在embedding dimension移动是没有意义的,所以你在做文字处理的时候,你只会在sentence顺序上移动filter,这个是另外的例子。
Reference

如果你想知道更多visualization事情的话,以上是一些reference。

如果你想要用Degree的方法来让machine自动产生一个digit,这件事是不太成功的,但是有很多其它的方法,可以让machine画出非常清晰的图。这里列了几个方法,比如说:PixelRNN,VAE,GAN来給参考.