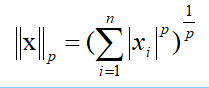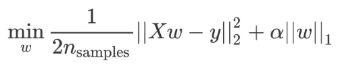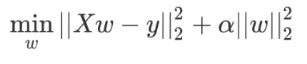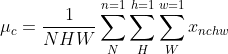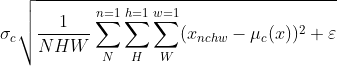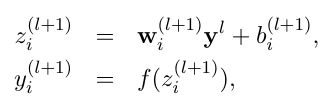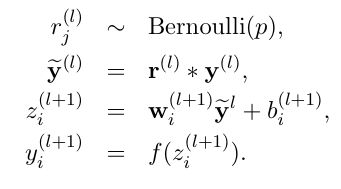【深度学习】正则化：L1正则化、L2正则化、Batch Normal与Dropout
目录
正则化
0 正则化介绍
0.0 什么是正则化？
0.1 正则化解决什么问题？
0.2 正则化常用手段
1 L1、L2正则化
1.0 范数定义
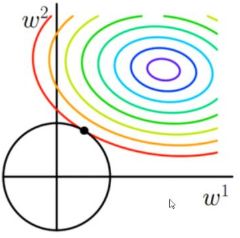
1.1 L1正则化（Ridge回归）
1.2 L2正则化（LASSO回归）
1.3 弹性网络
1.4 参考文献
2 Batch Normalization
2.0 BN介绍
2.1 Batch Normalization优缺点（作用）
2.2 BN的添加位置及限定
2.3 Pytorch框架中的具体实现
2.4 参考文献
3 Dropout
3.0 Dropout介绍
3.1 Dropout作用
3.2 Dropout率的设定
3.3 Dropout添加位置
3.4 Pytorch框架中的Dropout
3.5 参考文献
4 论文阅读
4.1 BN论文阅读
4.2 Dropout论文阅读
正则化
0 正则化介绍
0.0 什么是正则化？
《Deep Learning》书中定义正则化为“对学习算法的修改——旨在减少泛化误差而不是训练误差” 模型可以看成是一个高维函数，对于不同的模型参数，能得到千千万万个不同的模型，我们将这所有的可能得到的模型称之为假设空间。我们只需要通过训练将生成真实数据的一组模型参数找出来即可。从已有的假设空间中通过训练找到一个泛化能力优秀的拟合模型。正则化可以帮助我们从假设空间中找到这样一个模型：训练误差较低，测试误差较低，而且模型复杂度也较小。所以正则化是一种优化模型的方法。
就我目前的理解正则化其实就是能够正确指引网络学习方向的方法。比如说L1正则化、L2正则化，甚至损失函数都可以认为是正则化的一种手段。
0.1 正则化解决什么问题？
过拟合。
过拟合造成原因（导致方差过大）：
- 训练集和测试集的噪声数据分布不一致：训练集噪声和测试集噪声分布不一致。模型学到了训练集的噪声，但无法识别测试集的噪声。（Hinton在Dropout中提出的）
训练数据不足，参数量过大。
0.2 正则化常用手段
1）参数惩罚：L1称为lasso回归 L2称为Ridge回归
2）增强数据集：镜像，缩放，旋转
3）提前终止
4）多任务学习：MTCNN 增加任务（引入置信度）增加损失函数
5）dropout：理论上网络较深时，不会出现无任何神经元连接输出层
6）标准化：LRN、BN（Batch Normalization）等
1 L1、L2正则化
1.0 范数定义
范数是衡量某个向量空间（或矩阵）中的每个向量以长度或大小。范数的一般化定义：对实数p>=1， 范数定义如下：
当p=1时，是L1范数，其表示某个向量中所有元素绝对值的和。
当p=2时，是L2范数， 表示某个向量中所有元素平方和再开根， 也就是欧几里得距离公式。
什么是稀疏化？稀疏化指的是神经元的权重为0。
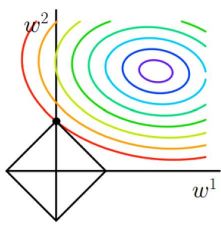
1.1 L1正则化（Ridge回归）
- 使用方式：
损失函数中加入L1正则项对W进行惩罚，抑制W，会使W抑制为0。 在剪枝时常用，平时训练时使用很可能导致网络稀疏化（退化）。
1.2 L2正则化（LASSO回归）
-
使用方式：
损失函数中加入L2正则项对W进行惩罚，抑制W。
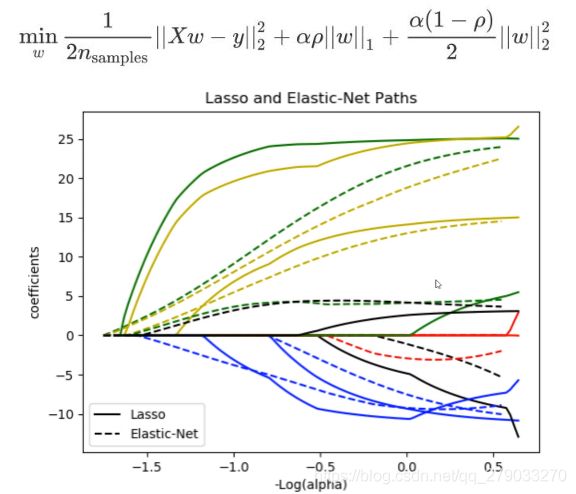
1.3 弹性网络
- 综合L1、L2正则化对网络优化。
1.4 参考文献
【博客 — L1、L2正则化详解】
【博客 — 机器学习中正则化项L1和L2的直观理解】
【博客 — 带约束的最优化问题】
2 Batch Normalization
2.0 BN介绍
Batch normalization是一种用于通过重新居中和重新缩放来对输入层进行规范化，从而使神经网络更快，更稳定的方法。
【Batch Normalization From Wikipedia】
通过减少隐藏层内部的变量偏移来加速网络的学习
论文： 【Batch Normalization】
2.1 Batch Normalization优缺点（作用）
优点：
1）对参数初始化的不敏感：在某些情况下可以取消 dropout 和 L2 正则项参数,或者采取更小的惩罚力度。由于BN会使隐藏层的输入维持在正太分布即输入都在[-1， 1]之间，即使当前层给予较大的w经过BN层后也会将数据拉回正太分布避免了梯度爆炸，避免梯度消失也同理。
2）对权重的尺度不再敏感：尺度同一由滑动系数γ决定。
3）减少了对学习率的要求：现在我们可以使用初始很大的学习率（或者选择了较小的学习率，算法也能够快速训练收敛——不知道是否正确）。
4）可以将bias置为0：因为标准化过程会移除直流分量，所以不再需要bias.
5）深度网络可以使用Sigmoid和tanh了：由于标准化和滑动系数，BN抑制了梯度消失。
< 破坏原来的数据分布，一定程度上缓解过拟合 >
缺点：
1）需要计算均值与方差，不适合动态网络或者RNN。
2）计算均值方差依赖每批次和大量的数据，批次较小时使用GN更好。
3）对于不符合正太分布的数据不适用。
2.2 BN的添加位置及限定
BN一般放在ReLU系列激活函数之前，Sigmoid和tanh激活含放在之后。但在实际使用中无太大区别。
BN和DropOut存在冲突，建议将其放在Dropout之前，并将Dropout率减小。（L2正则化与BN配合使用是否存在限制？）或者使用高斯Dropout的进阶版均值Dropout。
在使用时需要调net.eval()函数。
2.3 Pytorch框架中的具体实现
Pytorch框架在训练时，会统计所有批次的均值和方差；在测试时，会使用训练时统计的均值和方差对数据进行标准化，因为测试时很可能当前输入的batch_size为1，对于BN来说这是无法统计均值和方差的。所有批次的初始均值running_mean = 0、初始方差为running_var = 0，计算方式如下：
running_mean为以往样本加权求出的均值；running_var为以往样本加权求出的方差；momentum是一个参数为加权权重，默认值为0.1； μ为使用当前批次的所有样本求得的均值；σ为使用当前批次的所有样本求得的方差。
对于BN层测试的均值和方差是通过统计训练集的时候所有的batch的均值和方差的加权平均值。
-
-
-
对4D输入（具有可选附加通道尺寸的2D输入的小批量）应用Batch Normalization：
-
![y=\frac{x-E[x]}{\sqrt{Var[x]+\epsilon }}\ast \gamma +\beta](http://img.e-com-net.com/image/info8/585cc1d2a5264b8c85481936ef268071.gif)
-
在微型批次上按维度计算均值和方差，并且γ和β是维度大小为C的可学习参数向量（其中C为输入大小）。默认情况下，γ的元素设置为1，β的元素设置为0。通过有偏估计量计算标准差，相当于torch.var（input，unbiased = False）。
-
同样默认情况下，在训练过程中，该层会继续对其计算的均值和方差进行累加估算，然后将其用于推理阶段的标准化。 保持动态估算，默认动量momentum 为0.1。
-
如果track_running_stats设置为False，则此层将不保留运行时对均值和方差估计，而是在推理期间也只使用当前批的处理统计信息。
-
NOTE：
This
momentumargument is different from one used in optimizer classes and the conventional notion of momentum. Mathematically, the update rule for running statistics here is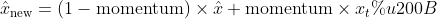
, where 
is the estimated statistic and 
is the new observed value.
-
-
参数：
-
-
num_features - 来自预期输入形状为（N，C，H, W)中的C
-
eps - 为分母增加数值的稳定性。默认值：1e-5
-
momentum – 用于动态计算训练时的均值和方差。可以设置
None只计算当前批次样本的均值和方差。默认值：0.1 -
affine – 一个布尔值，当设置
True为时，此模块具有可学习的仿射参数。若False则γ=1，β=0，gamma=1，beta=0，并且不能学习被更新。默认：True -
track_running_stats – 一个布尔值，设置为时
True，表示跟踪整个训练过程中所有batch的均值和方差统计信息，而不只是仅仅依赖与当前输入的batch的均值和方差；设置为时False，此模块不跟踪此模型所有样本的均值和方差统计信息，就只是计算当前输入的batch的均值和方差了了，且running_mean和running_var为None。当在推理阶段的时候，如果值为False，此时如果batch_size比较小，那么其均值和方差就会和全局均值和方差有着较大偏差。默认：True
-
-
形状：
-
-
输入: (N，C, H, W)
-
输出: 输出和输入同形状 (N，C, H, W)
-
2.4 参考文献
【博客 — 深入理解Batch Normalization批标准化】
【博客 — Pytorch-BN层详细解读】
【博客 — PyTorch中的Batch Normalization】
【知乎 — Batch Normalization原理与实战】
【pytorch框架 — torch.nn.BatchNorm2d】
3 Dropout
3.0 Dropout介绍
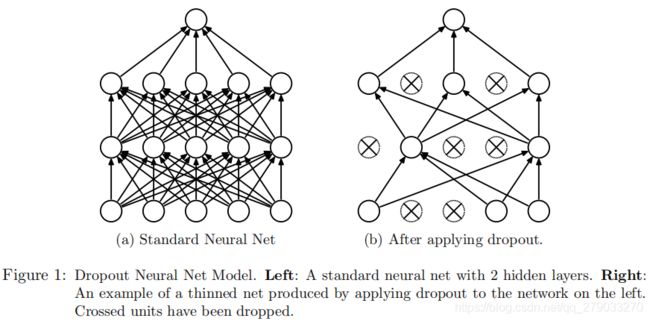
Dropout是Google提出的一种正则化技术，用以在人工神经网络中对抗过拟合。Dropout有效的原因，是它能够避免在训练数据上产生复杂的相互适应。Dropout这个术语代指在神经网络中丢弃部分神经元（包括隐藏神经元和可见神经元）。在训练阶段，dropout使得每次只有部分网络结构的参数得到更新，因而是一种高效的神经网络模型平均化的方法。维基百科Dropout
论文： 【Dropout: a simple way to prevent neural networks from overfitting】
3.1 Dropout作用
（1）取平均的作用： 先回到标准的模型即没有dropout，我们用相同的训练数据去训练5个不同的神经网络，一般会得到5个不同的结果，此时我们可以采用 “5个结果取均值”或者“多数取胜的投票策略”去决定最终结果。例如3个网络判断结果为数字9,那么很有可能真正的结果就是数字9，其它两个网络给出了错误结果。这种“综合起来取平均”的策略通常可以有效防止过拟合问题。因为不同的网络可能产生不同的过拟合，取平均则有可能让一些“相反的”拟合互相抵消。dropout掉不同的隐藏神经元就类似在训练不同的网络，随机删掉一半隐藏神经元导致网络结构已经不同，整个dropout过程就相当于对很多个不同的神经网络取平均。而不同的网络产生不同的过拟合，一些互为“反向”的拟合相互抵消就可以达到整体上减少过拟合。
（2）减少神经元之间复杂的共适应关系： 因为dropout程序导致两个神经元不一定每次都在一个dropout网络中出现。这样权值的更新不再依赖于有固定关系的隐含节点的共同作用，阻止了某些特征仅仅在其它特定特征下才有效果的情况 。迫使网络去学习更加鲁棒的特征 ，这些特征在其它的神经元的随机子集中也存在。换句话说假如我们的神经网络是在做出某种预测，它不应该对一些特定的线索片段太过敏感，即使丢失特定的线索，它也应该可以从众多其它线索中学习一些共同的特征。从这个角度看dropout就有点像L1，L2正则，减少权重使得网络对丢失特定神经元连接的鲁棒性提高。
（3）Dropout类似于性别在生物进化中的角色：物种为了生存往往会倾向于适应现存环境，环境突变则会导致物种难以做出及时反应，有性繁殖的出现可以繁衍出适应新环境的变种，单个基因组内部的协作被打破了，每个基因不仅要试着依靠自己来独立的控制各种生理功能，而且还要能与来自其他随机个体的基因一起协作，这两个要求使得每个基因都变得鲁棒，可以有效的阻止过拟合，即避免环境改变时物种可能面临的灭绝。
3.2 Dropout率的设定
Pytorch框架中dropout率越大惩罚力度越大。依据实际情况进行调整。
博客：隐藏层dropout率等于0.5的时候效果最好，原因是0.5的时候dropout随机生成的网络结构最多。
3.3 Dropout添加位置
网络层之后，激活函数之前。BN之后（和BN存在冲突 会使方差变得不一样，但现在一般只使用BN）。都在于添加噪声。（为什么是添加噪声？Dropout会剔除部分数据，起到遮挡的作用。）
3.4 Pytorch框架中的Dropout
-
Dropout2d
-
-
随机将整个通道置零（一个通道是一个二维的特征图，例如在一批输入的第个样本的第j个通道是一个二维张量输入[i, j]）。在每个前向调用过程中每个通道会按照从伯努利分布中采样的概率p独立地置零。
-
通常Dropout2d的输入来自于nn.Conv2d模块。
-
如论文Efficient Object Localization Using Convolutional Networks中提到的，如果特征图中的相邻像素是强相关的（浅层的卷积层通常是这样的），那么Dropout将不会使激活函数正则化而是仅仅导致学习率的有效降低。这种情况下，使用nn.Dropout2d()可以有效地提升特征图之间的独立性。
-
此外，再训练过程中输出被
因子进行了缩放。这意味着在评估过程中，该单元只是简单的计算了一个恒等函数。 -
参数
-
-
p - 元素置零的概率，默认为0.5
-
inplace - 如果设置为True，将会就地执行操作。默认为False
-
-
形状
-
-
输入：(N, C, H, W)
-
输出：(N, C, H, W)，和输入的形状一致
-
-
3.5 参考文献
【知乎 — 深度学习中Dropout原理解析】
【Pytorch — torch.nn.Dropout2D】
4 论文阅读
4.1 BN论文阅读
Abstract
神经网络训练非常复杂，因为在训练过程中，最初的输入会随着前向过程发生变化，导致隐藏层各层输入的分布也会发生变化。这减缓了设置了较低的学习率、严格参数初始化和具有饱和非线性激活函数的神经网络的训练。我们将这种情况称为内部协变量（协变量？）的偏移，并通过标准化每一层的输入来解决这个问题。这种方法的优势在于可以使用更高的学习率，并且对参数初始化不再那么敏感。它也起到了正则化的作用，并减少了在某些情况需要Dropout的情况。
1 Introduction
< 中间提到一大段关于SGD算法，暂时跳过； Mini-Batch SGD相对于One Example SGD的两个优势：梯度更新方向更准确；并行计算速度快；SGD训练的缺点：超参数调起来很麻烦。>
使用小批量的样本比使用单个样本多了以下好处：首先，小批量样本损失的梯度是对整个训练集梯度的估计，单批训练样本的质量随batch_size的增加而提高。其次，由于计算机的并行化处理设计，使得批量计算的效率远高于单个样本计算效率。
虽然随机梯度下降法简单有效，但它对网络模型的超参数、权重和学习率有较高的要求。每一层的输入都会受前面几层所有参数的影响，这使得训练变得复杂，且网络参数的微小变化会随着网络模型的加深而放大。
隐藏层输入分布的变化带来了后续层需要不断适应新的分布的问题。当输入到学习系统中的分布发生变化时，会被称为经验协变量偏移。而且这种偏移会在网络模型的各个部分发生。
固定子网络输入的分布对其他层也会产生积极影响。例如当激活函数时为饱和函数Sigmiod时，当|x|过大时会使梯度接近于0，网络将难以训练。这种负面影响随网络层的加深而增大，但在实际应用中可以通过ReLU激活函数、严格初始化和小的学习率来解决。然而，如果我们能够确保非线性输入的分布在网络训练时保持更稳定，那么优化器就不太可能陷入饱和状态，训练就会加速。
我们可以通过使用Batch Normalization消除网络内部输入的分布变换来实现给予网络较大的学习率进行训练。它通过一个标准化步骤修正了每层输入的平均值和方差。通过减少梯度对参数尺度（参数量）或参数初始值的依赖性，使得批处理归一化对网络梯度的反向传播也有有益的影响。这还使我们能够使用更高的学习率，而不会出现每层输入分布差异。此外，批量标准化正则化了模型，减少了辍学的需要（Srivastava等人，2014年）。最后，Batch Normalization可以通过防止网络输出陷入饱和区域使得我们可以使用饱和非线性的激活函数。
We refer to the change in the distributions of internal nodes of a deep network, in the course of training, as Internal Covariate Shift. Eliminating it offers a promise of faster training. We propose a new mechanism, which we call Batch Normalization, that takes a step towards reducing internal covariate shift, and in doing so dramatically accelerates the training of deep neural nets. It accomplishes this via a normalization step that fifixes the means and variances of layer inputs. Batch Normalization also has a benefificial effect on the gradient flflow through the network, by reducing the dependence of gradients on the scale of the parameters or of their initial values. This allows us to use much higher learning rates with out the risk of divergence. Furthermore, batch normalization regularizes the model and reduces the need for Dropout (Srivastava et al., 2014). Finally, Batch Normalization makes it possible to use saturating nonlinearities by preventing the network from getting stuck in the saturated modes.
2 Towards Reducing Internal Covariate Shift
我们将内部协变量转移定义为训练过程中由于网络参数的变化而引起的网络激活后分布的变化。为了改善训练，我们寻求减少内部协变量的偏移。通过在训练过程中固定隐藏层每层输入x的分布，可以提高训练速度。这一点是早就被发现的 (LeCun et al., 1998b; Wiesler & Ney, 2011) ，如果网络训练的输入被白化(whitened)，即将输入线性变换为零均值和单位方差，并进行去相关，则网络训练的收敛速度更快。
< 剩余部分讲了训练时遇到的一些问题 >
3 Normalization via Mini-Batch Statistics
使用BN必须使用批梯度下降即最小的batch_size要大于1。
BN将标准化每一批同一纬度的输入，使其均值为0方差为1。比如当前层的神经元如图 
，我们将标准化这一批数据1号神经元的输入，其次标准化这一批数据同时输入2号神经元的数据，最后，标准化这一批数据同时输入3号神经元的数据。按神经元的维度使用下面公式对数据进行标准化：![\hat{x}^{(k)}=\frac{{x}^{(k)} - E[{x}^{(k)}]}{\sqrt{Var[{x}^{(k)}]}}](http://img.e-com-net.com/image/info8/45e200caf764451693647ee477ba17ab.gif)
，其中
为单个神经的第k个输入。
值得注意的是当激活函数是Sigmoid或者tanh时，正则化可能使得激活后的输出分布在非线性函数的线性区域内。所以我们使标准化的输出为 
，其中γ和β是为了保证激活函数的非线性而设置的参数， 能使 偏移到非线性区域。而且γ和β是可学习的，由训练集整体决定。当 ![\gamma ^{(k)}=\sqrt{Var[x^{(k)}]}](http://img.e-com-net.com/image/info8/14870ef294ee49baad2d001cbe17e5a9.gif){kind=small}
和![\beta^{(k)}=E[x^{(k)}]](http://img.e-com-net.com/image/info8/94385e653b274c4eb1c56b1087c5eaa0.gif){kind=small}
时就会还原为BN前的分布。
小批次处理流程：
< 图1 >其中
为这一批数据。ε 为维持这一批样本方差的稳定性。 如果我们忽略ε和滑动系数
、
的话，每一层同一个神经元的输入都将是相同的分布。
3.1 Training and Inference with BatchNormalized Networks
在推理（使用）的时候，对于输入将会使用训练时的整体均值和方差使用 ![\hat{x} = \frac{x-E[x]}{\sqrt{Var[x] + \varepsilon }}](http://img.e-com-net.com/image/info8/4f7115e8160c4879aa6c131c0a7a2449.gif){kind=small}
进行标准化。其中![Var[x]=\frac{m}{m-1}\cdot E_{\beta }[\sigma ^{2}]](http://img.e-com-net.com/image/info8/c86a57613d46404ebb899bb1ddd50f34.gif){kind=small}
，m为Batch_size大小。
由于推理时使用的是固定的均值和方差，BN就简单地视作一个激活函数。
< 图2 >
3.2 Batch-Normalized Convolutional Networks
我们可以对输入层的输入使用BN，但是输入层的输入可能属于多峰分布（多高斯分布），而且在前两层使用BN并不会较少内部协变量的偏移。
注意到，我们对单个神经元的输出W·x+b进行了标准化，所以偏移量b是可以忽略的，因为偏移的作用包含在了公式 的中。所以我们可以将 
替换为
进行计算（公式中g为激活函数）。其中将BN变换独立应用于x = Wu的每个维度，每个维度具有一对独立的学习参数、。
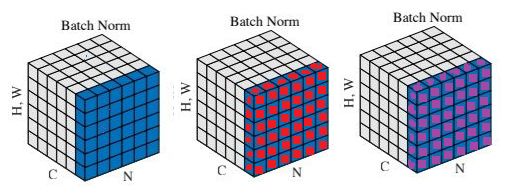
对于卷积网络来说，我们希望BN服从卷积属性。所以我们改变了< 图1 >中的 
为
，其中m为Batch_size，p、q为特征图的长宽。如下图中的有颜色的通道：
此时BN针对的就是同一通道的数据进行优化。计算公式如下：
、
和
上图和公式来自于：[博客 — 深入理解Batch Normalization]
3.3 Batch Normalization enables higher learning rates
未加BN的网络，过高的学习率可能会导致梯度消失和梯度爆炸，以及陷入局部最优解的情况。通过对整个网络进行标准化激活，可以防止网络参数的细微变化导致网络梯度的剧烈变化和陷入局部最优解的情况。
BN也使网络训练更能适应参数范围。通常情况下，大的学习速率会增加层参数的尺度，从而放大反向传播过程中的梯度，导致模型爆炸。但是，使用批处理规范化，通过层的反向传播不受其参数范围的影响。对于w放大α倍则经过BN后所得结果不变，即
我们可以看到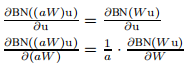 
标量α不影响雅克比(Jacobian 这是嘛？)矩阵和梯度的方向传播。更大权重导致较小的梯度，BN将稳定参数增长。 < 后面讲了雅克比矩阵相关的一些东西 >
3.4 Batch Normalization regularizes the model
当训练加入了BN的网络时，可见的是当前网络中的单个训练样本结合了同一批次的其他样本标准化后进行了训练，并且网络不再为当前的单个训练样本生成确定性的值，而是通过一批数据优化网络参数。这有利于提高网络的泛化力。而且我们可移除Dropout或降低Dropout的强度。
4.2 Dropout论文阅读
注：下文中很多公式实现以及图片和原论文中的不一样，是查看了现有框架的实现形式进行了调整
Abstract：
关键思想是抑制部分神经元，防止部分神经元过度配合（削弱大型网络模型神经元之间的相关性）。
训练时会从指数级别的模型空间抽取小型网络模型进行训练；测试时，通过一个未被抑制的拥有较小权重的网络，将所有小型网络的预测结果进行平均得到输出。
1. Introduction
过拟合的原因：对于少量数据集，大型网络会在训练时学习到训练集的噪声，但在测试集可能并不会拥有这些噪声。
在算力”无限“的理想情况下，我们”正则化“确定大小的模型的最佳方法是对参数的所有可能的预测输出求期望（均值），并根据已知训练集的后验概率对每个预测输出进行加权。此方法对小型网络有效。而在算力有限时，建议通过对近似共享参数网络模型（指数级别）的输出进行均等加权求其期望（均值）来实现。
模型组合总是能够提高机器学习的性能。将 使用同一训练集训练出的不同模型结构或通过不同训练集训练出的多个同一模型 进行合并对解决问题（正则化）最有帮助。但对于大型网络则不适用，因为每个大型网络结构不容易找到最优参数，而且训练通常需要大量算力和大量的数据集，还有在某些对性能要求较高的应用场景中会面临速度较慢的问题。
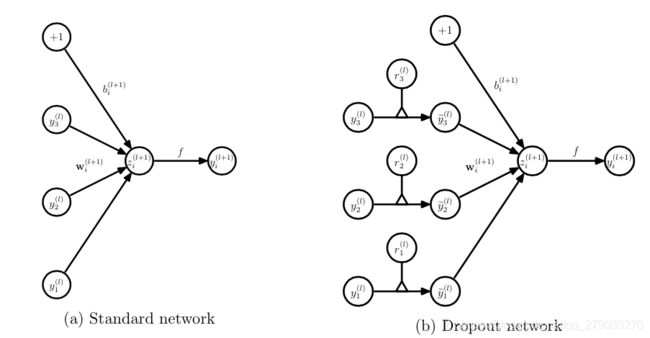
Dropout通过暂时随机地隐藏一部分神经元就可以解决上面遇到的问题。如下图：
每个神经元的隐藏事件是独立的，不受其他神经元的影响。其中隐藏概率P可通过测试集获得（如何获得？），或直接简单的设为0.5。但对于输入层的神经元通常设定的舍弃概率接近于0。
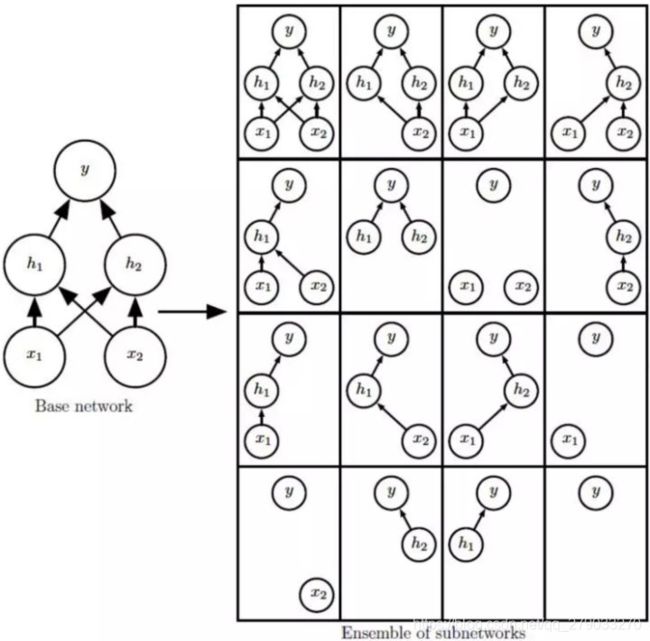
将Dropout应用到神经网络等同于从中采样由所“幸存”的神经元组成的小型网络 (Figure 1b)。具有n个单位的神经网络可以看做是个小型网络模型的集合。
而且这些网络共享权重，因此参数总量依旧是 
或者更少。
对于每个Batch都会采样一个新的小型网络进行训练。因此每个小型网络都有可能得到训练。
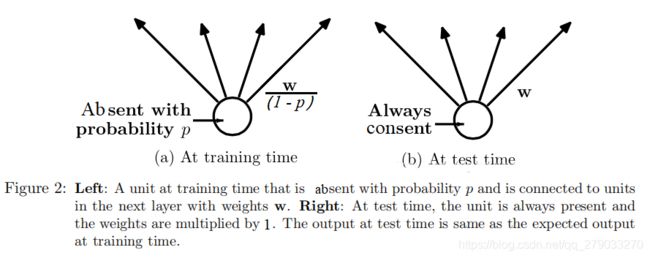
在训练时，我们需要对未被抑制的神经元输出乘以 1/(1-p) 进行缩放。原因是在测试时，我们显式的平均稀疏模型的预测是不可行的（测试时，模型是使用所有参数的）。那么我们可以在训练时，对预期输出进行缩放，确保缩放后的结果和测试时的实际输出分布相同。通过这种缩放，我们可以将具有共享权重的 
个网络合并成一个网络，以供其在测试时使用。与其他正则化方法相比，使用Dropout训练出的网络可以大大降低各种分类问题的泛化误差。
第2节描述了此想法的动机。第3节介绍了相关的先前工作。第4节正式介绍辍学模型。第5节给出了用于训练辍学网络的算法。在第6节中，我们介绍了我们的实验结果，其中我们将辍学应用于不同领域的问题，并将其与其他形式的正则化和模型组合进行了比较。第7节分析了辍学对神经网络不同属性的影响，并描述了辍学如何与神经网络的超参数相互作用。第8节介绍了Dropout RBM模型。在第9节中，我们探讨了使辍学边缘化的想法。
2. Motivation
Dropout源于生物学的有性生殖。有性繁殖通过打破基因之间的共适应性增强单组或单个基因的能力，并且使得有用的基因在整个种群中传播，来获取更好的应对环境变换的能力。而无性繁殖只会继承单个亲本具有良好协同的基因加少量基因突变，无种群内的基因组交换。而且目前大多数高级生物的进化方式都是有性繁殖，这就可能说明自然选择的可能不是基因组之间的协同性，而是组合能力。类似地，Dropout训练的神经网络中的每个隐藏单元必须学会与其他单元的随机选择的神经元一起工作。这应该可以使每个隐藏单元都更加强大，并促使其自行“进化”出有用的功能（学习到正确的权重），而不必依靠其他隐藏了的神经元来修正其偏移。而且因为隐藏具有随机性，单层中的所有隐藏单元可能在下一轮中会一起学习做其他事情。
One might imagine that the net would become robust against dropout by making many copies of each hidden unit, but this is a poor solution for exactly the same reason as replica codes are a poor way to deal with a noisy channel. A closely related, but slightly different motivation for dropout comes from thinking about successful conspiracies. Ten conspiracies each involving five people is probably a better way to create havoc than one big conspiracy that requires fifty people to all play their parts orrectly. If conditions do not change and there is plenty of time for rehearsal, a big conspiracy can work well, but with non-stationary conditions, the smaller the conspiracy the greater its chance of still working. Complex co-adaptations can be trained to work well on a training set, but on novel test data they are far more likely to fail than multiple simpler co-adaptations that achieve the same thing.
上面这段话（可能）的大致意思是：5个人的10次 破坏可能比50个人的1次破坏更好。如果条件不变，有足够的时间进行训练，50人一次破坏可以很好地发挥作用，但在非平稳条件下，规模越小，仍然发挥作用的机会就越大。多神经元的协同适应可以在一个训练集上训练得很好，但在新的测试数据上，它们比实现相同目标的多个简单的协同适应失败的可能性大得多。
3. Related Work
Dropout可以解释为一种通过向其隐藏单元添加噪声来规范化神经网络的方法（原想法来自于向自编码结构的输入加入噪声，而目标是未加噪声的输入）。实验表明Dropout可以有效地应用于隐藏层，也可以将其解释为一种形式的模型平均。而且添加噪声不仅对无监督的特征学习有用，而且可以推广到有监督的学习问题。通常去掉20%的输入单元和50%的隐藏单元是最优的。
由于Dropout可以被看作是一种随机正则化技术，自然地考虑通过边缘化噪声得到它的相反物——确定性的正则化。
Since dropout can be seen as a stochastic regularization technique, it is natural to consider its deterministic counterpart which is obtained by marginalizing out the noise. In this paper, we show that, in simple cases, dropout can be analytically marginalized out to obtain deterministic regularization methods.
In dropout, we minimize the loss function stochastically under a noise distribution.This can be seen as minimizing an expected loss function.
< 未知 >
4. Model Description
4.1 训练阶段
1）没有dropout的神经网络
2）有dropout的神经网络
和普通网络的区别：
5. Learning Dropout Nets
本节描述了训练Dropout神经网络的过程。
5.1 Backpropagation
加入Dropout的网络的正向和反向传播仅在当前小型网络上进行。每个参数的梯度在每个小批量的训练案例中平均的。任何不使用该参数的小型网络都不会为修正该参数。
One particular form of regularization was found to be especially useful for dropout——constraining the norm of the incoming weight vector at each hidden unit to be upper bounded by a fixed constant c. In other words, if w represents the vector of weights incident on any hidden unit, the neural network was optimized under the constraint
≤ c. This constraint was imposed during optimization by projecting w onto the surface of a ball of radius c, whenever w went out of it. This is also called max-norm regularization since it implies that the maximum value that the norm of any weight can take is c. The constant c is a tunable hyperparameter, which is determined using a validation set. Max-norm regularization has been previously used in the context of collaborative filtering (Srebro and Shraibman, 2005). It typically improves the performance of stochastic gradient descent training of deep neural nets, even when no dropout is used.
Although dropout alone gives significant improvements, using dropout along with maxnorm regularization, large decaying learning rates and high momentum provides a significant boost over just using dropout. A possible justification is that constraining weight vectors to lie inside a ball of fixed radius makes it possible to use a huge learning rate without the possibility of weights blowing up. The noise provided by dropout then allows the optimization process to explore different regions of the weight space that would have otherwise been difficult to reach. As the learning rate decays, the optimization takes shorter steps, thereby doing less exploration and eventually settles into a minimum.
< 不知道现在框架是否有用到上面提到的 >
5.2 Unsupervised Pretraining
在某些情况下，训练预训练过的网络比训练随机初始化的网络，具有显著的性能提升。
Dropout也可以用于这些与训练过的网络，但是可能会抹去预训练的权重。解决方法是在训练时给予网络较小的学习率似乎能保留预训练的权重。
6 拓展
集成学习（Ensemble Learning）是使用多个机器学习模型进行学习，并使用某种规则把各个学习结果进行整合从而获得比单个学习器更好的学习效果的一种机器学习方法，相对于单个分类器作为决策者，集成学习的方法就相当于多个决策者共同进行一项决策。例如：Bagging算法（装袋算法），它分别训练几个基学习器，然后让所有基学习器表决最终的输出，被称为模型平均（model averaging）
[博客 — 一文看懂集成学习]
更新日志：
2020/11/14 --- 更新正则化介绍、L1和L2正则化，以及Batch Normalization
2020/11/15 --- 更新整体结构、更新Dropout
作者：阳一子
本文地址：https://blog.csdn.net/qq_279033270/article/details/109695441