2020_TKDE_DiffNet++_A Neural Influence and Interest Diffusion Network for Social Recommendation
[论文阅读笔记]2020_TKDE_DiffNet++_A Neural Influence and Interest Diffusion Network for Social Recommendation
论文下载地址: https://arxiv.org/abs/2002.00844v2
发表期刊:TKDE
Publish time: 2020
作者及单位:
- Le Wu, Member, IEEE, Junwei Li, Peijie Sun, Richang Hong, Member, IEEE, Y ong Ge, Member, IEEE, Meng Wang, Fellow, IEEE
数据集: 正文中的介绍
- Yelp https://www.yelp.com/dataset
- Flickr http://flickr.com/
- Epinions [http://www.trustlet.org/downloaded epinions.html](http://www.trustlet.org/downloaded epinions.html)
- Dianping https://lihui.info/data/
代码:
- https://github.com/PeiJieSun/diffnet (文中作者给的。DiffNet没给,就是等着今年发了这篇才给)
其他:
其他人写的文章
简要概括创新点: 作者们去年发了DiffNet(只考虑的Social Network),今年再发DiffNet++(再考虑上user-item interset Network).
- (1)we propose DiffNet++, an improved algorithm of DiffNet that models the neural influence diffusion and interest diffusion in a unified framework. (我们提出了DiffNet++,这是一种改进的DiffNet算法,它在一个统一的框架中对神经影响扩散和兴趣扩散进行建模。)
- (2)By reformulating the social recommendation as a heterogeneous graph with social network and interest network as input, DiffNet++ advances DiffNet by injecting both the higher-order user latent interest reflected in the user-item graph and higher-order user influence reflected in the user-user graph for user embedding learning. (DiffNet++通过将社会推荐转化为一个以社会网络和兴趣网络为输入的异构图,将反映在user-item图中的高阶用户潜在兴趣和反映在user-user图中的高阶用户影响注入DiffNet,以进行用户嵌入学习。)
- (3)This is achieved by iteratively aggregating each user’s embedding from three aspects: (这是通过从三个方面迭代聚合每个用户的嵌入来实现的:)
- the user’s previous embedding, (用户之前的嵌入,)
- the influence aggregation of social neighbors from the social network, (社交网络中社交邻居的影响力聚集)
- and the interest aggregation of item neighbors from the user-item interest network. (来自用户项目兴趣网络的项目邻居的兴趣聚合。)
- (4)Furthermore, we design a multi-level attention network that learns how to attentively aggregate user embeddings from these three aspects. (此外,我们设计了一个多层次的注意网络,学习如何从这三个方面区分注意力地集中用户嵌入)
Abstract
- (1) Social recommendation has emerged to leverage social connections among users for predicting users’ unknown preferences, which could alleviate the data sparsity issue in collaborative filtering based recommendation. (社交推荐利用用户之间的社交关系来预测用户的未知偏好,这可以缓解基于协同过滤的推荐中的数据稀疏问题。)
- (2) Early approaches relied on utilizing each user’s first-order social neighbors’ interests for better user modeling, and failed to model the social influence diffusion process from the global social network structure. (早期的方法依赖于利用每个用户的一阶社交邻居的兴趣进行更好的用户建模,而未能从全球社交网络结构中建模社会影响扩散过程。)
- (3) Recently, we propose a preliminary work of a neural influence Diffusion Network (i.e., DiffNet) for social recommendation [43]. DiffNet models the recursive social diffusion process for each user, such that the influence diffusion hidden in the higher-order social network is captured in the user embedding process. Despite the superior performance of DiffNet, we argue that, as users play a central role in both user-user social network and user-item interest network, only modeling the influence diffusion process in the social network would neglect the latent collaborative interests of users hidden in the user-item interest network. (最近,我们提出了一个用于社会推荐的神经影响扩散网络(即DiffNet)的初步工作[43]。DiffNet为每个用户建模递归的社会扩散过程,从而在用户嵌入过程中捕获隐藏在高阶社会网络中的影响扩散。尽管DiffNet的性能优越,但我们认为,由于用户在用户-用户-社交网络和用户项目-兴趣网络中都扮演着核心角色,因此仅对社交网络中的影响扩散过程进行建模将忽略隐藏在用户项目-兴趣网络中的用户的潜在协作兴趣。)
- (4) To this end, in this paper, we propose DiffNet++, an improved algorithm of DiffNet that models the neural influence diffusion and interest diffusion in a unified framework. (我们提出了DiffNet++,这是一种改进的DiffNet算法,它在一个统一的框架中对神经影响扩散和兴趣扩散进行建模。)
- By reformulating the social recommendation as a heterogeneous graph with social network and interest network as input, DiffNet++ advances DiffNet by injecting both the higher-order user latent interest reflected in the user-item graph and higher-order user influence reflected in the user-user graph for user embedding learning. (DiffNet++通过将社会推荐转化为一个以社会网络和兴趣网络为输入的异构图,将反映在user-item图中的高阶用户潜在兴趣和反映在user-user图中的高阶用户影响注入DiffNet,以进行用户嵌入学习。)
- This is achieved by iteratively aggregating each user’s embedding from three aspects: (这是通过从三个方面迭代聚合每个用户的嵌入来实现的:)
- the user’s previous embedding, (用户之前的嵌入,)
- the influence aggregation of social neighbors from the social network, (社交网络中社交邻居的影响力聚集)
- and the interest aggregation of item neighbors from the user-item interest network. (来自用户项目兴趣网络的项目邻居的兴趣聚合。)
- Furthermore, we design a multi-level attention network that learns how to attentively aggregate user embeddings from these three aspects. (此外,我们设计了一个多层次的注意网络,学习如何从这三个方面区分注意力地集中用户嵌入)
- Finally, extensive experimental results on four real-world datasets clearly show the effectiveness of our proposed model. We release the source code at https://github.com/PeiJieSun/diffnet. (最后,在四个真实数据集上的大量实验结果清楚地表明了我们提出的模型的有效性。我们在https://github.com/PeiJieSun/diffnet.)
Index Terms
recommender systems, graph neural network, social recommendation, influence diffusion, interest diffusion
1 INTRODUCTION
-
(1) Collaborative Filtering (CF) based recommender systems learn user and item embeddings by utilizing user-item interest behavior data, and have attracted attention from both the academia and industry [37], [32]. However, as most users have limited behavior data, CF suffers from the data sparsity issue [1]. With the development of social networks, users build social relationships and share their item preferences on these platforms. As well supported by the social influence theory, users in a social network would influence each other, leading to similar preferences [12], [2]. Therefore, social recommendation has emerged, which focuses on exploiting social relations among users to alleviate data sparsity and enhancing recommendation performance [19], [20], [14], [43]. (基于协同过滤(CF)的推荐系统通过利用用户项目兴趣行为数据来学习用户和项目嵌入,已经引起了学术界和工业界的关注[37],[32]。然而,由于大多数用户的行为数据有限,CF存在数据稀疏问题[1]。随着社交网络的发展,用户在这些平台上建立社交关系并分享他们的商品偏好。社交网络中的用户会相互影响,从而产生相似的偏好[12],[2],这也得到了社会影响理论的支持。因此,社交推荐应运而生,其重点是利用用户之间的社交关系来缓解数据稀疏性,并提高推荐性能[19]、[20]、[14]、[43]。)
-
(2) In fact, as users play a central role in social platforms with user-user social behavior and user-item interest behavior, the key to social recommendation relies on learning user embeddings with these two kinds of behaviors. (事实上,由于用户在社交平台中扮演着核心角色,具有用户社交行为和用户项目兴趣行为,社交推荐的关键在于学习用户嵌入这两种行为。)
- For a long time, by treating the user-item interest network as a user-item matrix, CF based models resort to matrix factorization to project both users and items into a low latent space [37], [32], [36]. (长期以来,通过将用户项目兴趣网络视为用户项目矩阵,基于CF的模型采用矩阵分解,将用户和项目投影到一个低潜在空间[37]、[32]、[36]。)
- Most social based recommender systems advance these CF models by leveraging the user-user matrix to enhance each user’s embedding learning with social neighbors’ records, (大多数基于社交的推荐系统通过利用用户矩阵来增强每个用户对社交邻居记录的嵌入学习,从而推进这些CF模型,)
- or regularizing the user embedding learning process with social neighbors [19], [30], [21], [15]. For example, SocialMF [19] and SR [30] added social regularization terms based on social neighbors in the optimization function, and TrustSVD incorporated influences of social neighbors’ decisions as additional terms for modeling a user’s embedding [15]. (或者通过社交邻居规范用户嵌入学习过程[19]、[30]、[21]、[15]。例如,SocialMF[19]和SR[30]在优化函数中添加了基于社会邻居的社会正则化项,而TrustSVD将社会邻居的决策的影响作为建模用户嵌入的附加项[15]。)
- In summary, these models leveraged the first-order social neighbors for recommendation, and partially alleviated the data sparsity issue in CF. (总之,这些模型利用一阶社交邻居进行推荐,部分缓解了CF中的数据稀疏问题。)

-
(3) Despite the performance improvement of these social recommendation models, we argue that the current social recommendation models are still far from satisfactory. (尽管这些社会推荐模型的性能有所提高,但我们认为目前的社会推荐模型仍然远远不能令人满意。)
-
In fact, as shown in Fig. 1, users play a central role in two kinds of behavior networks: the user-user social network and the user-item interest network. (事实上,如图1所示,用户在两种行为网络中扮演着核心角色:用户社交网络和用户项目兴趣网络。)
- On one hand, users naturally form a social graph with a global recursive social diffusion process. Each user is not only influenced by the direct first-order social neighbors, but also the higher-order ego-centric social network structure. E.g., though user u1 does not follow u5, u1 may be largely influenced by u5 in the social recommendation process as there are two second-order paths: u1 → u2 → u5 and u1 → u4 → u5. Simply reducing the social network structure to the first-order social neighbors would not well capture these higher-order social influence effect in the recommendation process. (一方面,用户自然形成一个具有全局递归社会扩散过程的社会图。每个用户不仅受到直接的一阶社交邻居的影响,还受到更高阶的以自我为中心的社交网络结构的影响。例如,虽然用户u1不遵循u5,但u1在社交推荐过程中可能会受到u5的很大影响,因为有两条二阶路径:u1→ u2→ u5和u1→ u4→ u5。简单地将社交网络结构简化为一阶社交邻居并不能在推荐过程中很好地捕捉到这些高阶社会影响效应)
- On the other hand, given the user-item bipartite interest graph, CF relies on the assumption that “similar users show similar item interests”. Therefore, each user’s latent collaborative interests are not only reflected by her rated items but also influenced by similar users’ interests from items. E.g, though u1 does not show interests for v3 with a direct edge connection, the similar user u2 (as they have common item interests of v1) shows item interest for v3 as: u1 ↔ v1 ↔ u2 ↔ v3. Therefore, v3 is also useful for learning u1’s embedding to ensure the collaborative signals hidden in the user-item graph are injected for user embedding learning. (另一方面,给定用户项目二部兴趣图,CF依赖于“相似用户显示相似项目兴趣”的假设。因此,每个用户的潜在合作兴趣不仅反映在她的评分项目上,而且还受到来自项目的相似用户兴趣的影响。例如,虽然u1没有显示对直接边缘连接的v3感兴趣,但类似的用户u2(因为他们对v1有共同的项目兴趣)将v3的项目兴趣显示为:u1↔ v1↔ u2↔ v3。因此,v3也有助于学习u1的嵌入,以确保隐藏在用户项图中的协作信号被注入用户嵌入学习。)
- To summarize, previous CF and social recommendation models only considered the observed first-order structure of the two graphs, leaving the higher-order structures of users under explored. (综上所述,以前的CF和社交推荐模型只考虑了观察到的两个图的一阶结构,没有充分研究用户的高阶结构。)
-
(4) To this end, we reformulate users’ two kinds of behaviors as a heterogeneous network with two graphs, i.e, a user-user social graph and a user-item interest graph, and propose how to explore the heterogeneous graph structure for social recommendation.
-
In fact, Graph Convolutional Networks (GCNs) have shown huge success for learning graph structures with theoretical elegance, practical flexibility and high performance [5], [8], [22]. GCNs perform node feature propagation in the graph, which recursively propagate node features by iteratively convolutional aggregations from neighborhood nodes, such that the up to K-th order graph structure is captured with K iterations [47]. (事实上,图卷积网络(GCN)在学习图结构方面取得了巨大的成功,具有理论上的优雅、实用的灵活性和高性能[5]、[8]、[22]。GCN在图中执行节点特征传播,通过迭代卷积聚合从邻域节点递归传播节点特征,从而通过K次迭代捕获高达K阶的图结构[47]。)
-
By treating user-item interactions as a bipartite interest graph and user-user social network as a social graph, some works have applied GCNs separately on these two kinds of graphs [51], [41], [48], [43]. (通过将用户项目交互视为一个二分兴趣图,将用户社交网络视为一个社交图,一些研究将GCN分别应用于这两类图[51]、[41]、[48]、[43]。)
- On one hand, given the user-item interest graph, NGCF is proposed to directly encode the collaborative information of users by exploring the higher-order connectivity patterns with embedding propagation [41]. (一方面,在给定用户项目兴趣图的情况下,NGCF 通过嵌入传播探索高阶连通模式,直接编码用户的协作信息[41]。)
- On the other hand, in our previous work, we propose a Diffusion neural Network (DiffNet) to model the recursive social diffusion process in the social network, such that the higher-order social structure is directly modeled in the recursive user embedding process [43]. (另一方面,在我们之前的工作中,我们提出了一种 扩散神经网络(DiffNet) 来模拟社会网络中的递归社会扩散过程,从而在递归用户嵌入过程中直接模拟高阶社会结构[43]。)
- These graph based models( showed superior performance compared to the previous non-graph based recommendation models by modeling either graph structure. Nevertheless, how to design a unified model for better user modeling of these two graphs remains under explored. (与以前的非基于图的推荐模型相比,这些 基于图的模型 通过对两种图结构进行建模,表现出了更好的性能。然而,如何设计一个统一的模型来更好地为这两个图进行用户建模仍有待探索。)
-
(5) In this paper, we propose to advance our preliminary DiffNet structure, and jointly model the two graph structure (user-item graph and user-user graph) for social recommendation. (在本文中,我们提出了我们初步的DiffNet结构,并为社会推荐的两种图结构(用户项目图和用户用户图)联合建模。)
- While it seems intuitive to perform message passing on both each user’s social network and interest network, it is not well designed in practice as these two kinds of graphs serve as different sources to reflect each user’s latent preferences. (虽然在每个用户的社交网络和兴趣网络上执行消息传递似乎很直观,但在实践中设计得并不好,因为这两种图形作为不同的来源来反映每个用户的潜在偏好。)
- Besides, different users may have different preferences in balancing these two graphs, with some users are likely to be swayed by social neighbors, while others prefer to remain their own tastes. (此外,不同的用户在平衡这两张图时可能有不同的偏好,一些用户可能会受到社交邻居的影响,而其他用户则更喜欢保持自己的品味。)
-
To this end, we propose DiffNet++, an improved algorithm of DiffNet that models the neural influence diffusion and interest diffusion in a unified framework. (为此,我们提出了DiffNet++,这是一种改进的DiffNet算法,它在一个统一的框架中对神经影响扩散和兴趣扩散进行建模。)
-
Furthermore, we design a multi-level attention network structure that learns how to attentively aggregate user embeddings from different nodes in a graph, and then from different graphs. (此外,我们设计了一个多层次的注意网络结构,学习如何专注地聚合来自图中不同节点的用户嵌入,然后再从不同的图中聚合。)
-
(6) In summary, our main contributions are listed as follows:
- Compared to our previous work of DiffNet [43], we revisit the social recommendation problem as predicting the missing edges in the user-item interest graph by taking both user-item interest graph and user-user social graph as input. (与DiffNet[43]之前的工作相比,我们将社交推荐问题重新考虑为通过将用户项目兴趣图和用户-用户社交图作为输入来预测用户项目兴趣图中缺失的边。)
- We propose DiffNet++ that models both the higher-order social influence diffusion in the social network and interest diffusion in the interest network in a unified model. (我们提出DiffNet++在一个统一的模型中对社会网络中的高阶社会影响扩散和兴趣网络中的兴趣扩散进行建模。)
- Besides, we carefully design a multi-level attention network to attentively learn how the users prefer different graph sources. (此外,我们还精心设计了一个多层次的注意网络,仔细了解用户对不同图源的偏好。)
-
Extensive experimental results on two real-world datasets clearly show the effectiveness of our proposed DiffNet++ model. Compared to the baseline with the best performance, DiffNet++ outperforms it (在两个真实数据集上的大量实验结果清楚地表明了我们提出的DiffNet++模型的有效性。与性能最好的基线相比,DiffNet++的性能优于它)
2 PROBLEM DEFINITION AND RELATED WORK
2.1 Problem Definition
-
(1) In a social recommender system, there are two sets of entities: a user set U U U (|U|=M), and an item set V V V (|V |=N). Users form two kinds of behaviors in the social platforms: making social connections with other users and showing item interests.
- These two kinds of behaviors could be defined as two matrices: a user-user social connection matrix S ∈ R M × M S \in R^{M\times M} S∈RM×M, and a user-item interaction matrix R ∈ R M × N R \in R^{M\times N} R∈RM×N.
- In the social matrix S S S, if user a a a trusts or follows user b b b, s b a = 1 s_{ba} = 1 sba=1, otherwise it equals 0.
- We use S a S_a Sa to represent the user set that user a a a follows, i.e., S a = [ b ∣ s b a = 1 ] . S_a= [b|s_{ba} = 1]. Sa=[b∣sba=1].
- The user-item matrix R R R shows users’ rating preferences and interests to items. (用户项目矩阵R显示用户对项目的评分偏好和兴趣。)
- As some implicit feedbacks (e.g., watching movies, purchasing items, listening to songs ) are more common in real-world applications, we also consider the recommendation scenario with implicit feedback [37]. (由于一些隐含的反馈(例如,观看电影,购买物品,听歌曲)在现实世界中的应用更为普遍,我们也考虑隐含反馈的推荐场景[37 ]。)
- Let R R R denote users’ implicit feedback based rating matrix, with r a i = 1 r_{ai} = 1 rai=1 if user a a a is interested in item i i i, otherwise it equals 0.
- We use R a R_a Ra represents the item set that user a a a has consumed, i.e., R a = [ i ∣ r a i = 1 ] R_a= [i | r_{ai} = 1] Ra=[i∣rai=1],
- and R i R_i Ri denotes the user set which consumed the item i i i, i.e., R i = [ a ∣ r i a = 1 ] R_i = [a|r_{ia} = 1] Ri=[a∣ria=1].
-
(2) Given the two kinds of users’ behaviors, the user-user social network is denoted as a user-user directed graph: G S = < U , S > GS=< U,S > GS=<U,S>,
- where U U U is the nodes of all users in the social network. If the social network is undirected, then user a a a connects to user b b b denotes a a a follows b b b, and b b b also follows a a a, i.e., s a b = 1 ∧ s b a = 1 s_{ab} = 1\land s_{ba} = 1 sab=1∧sba=1.
-
The user interest network denotes users’ interests for items, which could be constructed from the user-item rating matrix R R R as an undirected bipartite network: G I = < U ∪ V , R > G_I = < U \cup V, R > GI=<U∪V,R>.
-
(3) Besides, each user a a a is associated with real-valued attributes (e.g, user profile), denoted as x a x_a xa in the user attribute matrix X ∈ R d 1 × M X \in R^{d1\times M} X∈Rd1×M.
- Also, each item i i i has an attribute vector y i y_i yi(e.g., item text representation, item visual representation) in item attribute matrix Y ∈ R d 2 × N Y \in R^{d2\times N} Y∈Rd2×N. We formulate the graph based social recommendation problem as:
Definition 1 (Graph Based Social Recommendation).
- (1) Given the user social network G_S and user interest network G_I, these two networks could be formulated as a heterogeneous graph that combines G S G_S GS and G I G_I GI as: G = G S ∪ G I = < U ∪ V , X , Y , R , S > G = G_S \cup G_I = < U \cup V, X, Y, R, S > G=GS∪GI=<U∪V,X,Y,R,S>.
- Then, the graph based social recommendation asks that: given graph G G G in the social network, our goal is to predict users’ unknown preferences to items , i.e, the missing links in the graph based social recommendation as : R ^ = f ( G ) = f ( U ∪ V , X , Y , R , S ) \hat{R} = f(G) = f(U \cup V, X, Y, R, S) R^=f(G)=f(U∪V,X,Y,R,S), where R ^ ∈ R M × N \hat{R} \in R^{M\times N} R^∈RM×N denotes the predicted preferences of users to items.
2.2 Preliminaries and Related Work
In this subsection, we summarize the related works for social recommendation into three categories: classical social recommendation models, the recent graph based recommendation models, and attention modeling in the recommendation domain. (在这一小节中,我们将社会推荐的相关工作归纳为三类:经典的社会推荐模型、最新的基于图的推荐模型和推荐领域中的注意建模。)
2.2.1 Classical Social Recommendation Models.
-
(1) By formulating users’ historical behavior as a user-item interaction matrix R, most classical CF models embed both users and items in a low dimension latent space, such that each user’s predicted preference to an unknown item turns to the inner product between the corresponding user and item embeddings as [37], [32], [36]: (通过将用户的历史行为表述为用户-项目交互矩阵R,大多数经典CF模型将用户和项目嵌入到低维潜在空间中,使得每个用户对未知项目的预测偏好转向相应用户和项目嵌入之间的内积[37]、[32]、[36]:)

- where u a u_a ua is the embedding of user a a a, which is the a a a-th column of the user embedding matrix U U U. Similarly , virepresents item i i i’s embedding in the i i i-th column of item embedding matrix V V V.
-
(2) In fact, as various specialized matrix factorization models have been proposed for specific tasks, factorization machines is proposed as a general approach to mimic most factorization models with simple feature engineering [36]. Recently, some deep learning based models have been proposed to tackle the CF problem [17], [28]. These approaches advanced previous works by modeling the non-linear complex interactions between users, or the complex interactions between sparse feature input. (事实上,由于针对特定任务提出了各种专门的矩阵分解模型,分解机被提议作为一种通用方法,用简单的特征工程模拟大多数分解模型[36]。最近,有人提出了一些基于深度学习的模型来解决CF问题[17],[28]。这些方法通过建模用户之间的非线性复杂交互,或稀疏特征输入之间的复杂交互,推进了以前的工作。)
-
(3) The social influence and social correlation among users’ interests are the foundation for building social recommender systems[29], [38], [25], [24]. Therefore, the social network among users could be leveraged to alleviate the sparsity in CF and enhance recommendation performance [30], [38], [15]. Due to the superiority of embedding based models for recommendation, most social recommendation models are also built on these embedding models. (用户兴趣的社会影响和社会关联是构建社会推荐系统的基础[29 ]、[38 ]、[25 ]、[24 ]。因此,可以利用用户之间的社交网络来缓解CF中的稀疏性,并提高推荐性能[30]、[38]、[15]。由于基于嵌入的推荐模型的优越性,大多数社会推荐模型也建立在这些嵌入模型的基础上。)
-
These social embedding models could be summarized into the following two categories: (这些社会嵌入模型可归纳为以下两类:)
- the social regularization based approaches [19], [30], [21], [26], [44] (基于社会正则化的方法)
- and the user behavior enhancement based approaches [14], [15]. (基于用户行为增强的方法)
- Specifically, the social regularization based approaches assumed that connected users would show similar embeddings under the social influence diffusion. (基于社会规范化的方法假设在社会影响扩散下,有联系的用户会表现出相似的嵌入。)
- As such, besides the classical CF pair-wised loss function in BPR [37], an additional social regularization term is incorporated in the overall optimization function as:
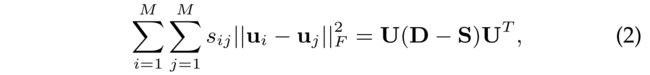
- where D D D is a diagonal matrix with d a a = ∑ b = 1 M s a b d_{aa} = \sum^{M}_{b=1}s_{ab} daa=∑b=1Msab. (D是对角矩阵)
-
(4) Instead of the social regularization term, some researchers argued that the social network provides valuable information to enhance each user’s behavior [50], [15]. TrustSVD is such a representative model that shows state-of-the-art performance [14], [15]. By assuming the implicit feedbacks of a user’s social neighbors’ on items could be regarded as the auxiliary feedback of this user, TrustSVD modeled the predicted preference as: (一些研究人员认为,社交网络提供了有价值的信息来增强每个用户的行为,而不是社交规范化术语[50],[15]。TrustSVD就是这样一个具有代表性的模型,它展示了最先进的性能[14],[15]。通过假设用户的社交邻居对项目的隐性反馈可以被视为该用户的辅助反馈,TrustSVD将预测偏好建模为:)

- where R a = [ i ∣ r a i = 1 ] R_a= [i | r_{ai} = 1] Ra=[i∣rai=1] is the itemset that a shows implicit feedback, and y i y_i yi is an implicit factor vector. Therefore, these first two terms compose SVD++ model that explicitly builds each user’s liked items in the user embedding learning process [23]. In the third term, u b u_b ub denotes the latent embedding of user b b b, who is trusted by a a a. As such, a a a’s latent embedding is enhanced by considering the influence of her trusted users’ latent embeddings in the social network. (因此,前两项构成了SVD++模型,该模型在用户嵌入学习过程中显式地构建每个用户喜欢的项目[23]。在第三项中, u b u_b ub表示用户 b b b的潜在嵌入,用户 b b b受 a a a信任。因此, a a a的潜在嵌入通过考虑其受信任用户在社交网络中的潜在嵌入的影响而增强。)
-
(5) As items are associated with attribute information (e.g., item description, item visual information), ContextMF is proposed to combine social context and social network under a collective matrix factorization framework with carefully designed regularization terms [21]. (由于项目与属性信息(如项目描述、项目视觉信息)相关联,ContextMF被提议在一个集体矩阵分解框架下结合社会背景和社会网络,并使用精心设计的正则化术语[21]。)
-
Social recommendation has also been extended with social circles [34], temporal context [38], rich contextual information [42], user role in the social network [39], and efficient training models without negative sampling [6]. All these previous works focused on how to explore the social neighbors, i.e., the observed links in the social network. (社交圈[34]、时间上下文[38]、丰富的上下文信息[42]、社交网络中的用户角色[39]以及无负采样的高效培训模型[6]也扩展了社交推荐。所有这些之前的工作都集中在如何探索社交邻居,即社交网络中观察到的链接。)
-
Recently, CNSR is proposed to leverage the global social network in the recommendation process [44]. In CNSR, each user’s latent embedding is composed of two parts: (最近,CNSR被提议在推荐过程中利用全球社交网络[44]。在CNSR中,每个用户的潜在嵌入由两部分组成:)
- a free latent embedding (classical CF models), (自由潜在嵌入(经典CF模型),)
- and a social network embedding that captures the global social network structure. (以及一个社交网络嵌入,捕捉全球社交网络结构。)
- Despite the relative improvement of CNSR, we argue that CNSR is still suboptimal as the global social network embedding process is modeled for the network based optimization tasks instead of user preference learning. (尽管CNSR相对有所改进,但我们认为,CNSR仍然是次优的,因为全局社会网络嵌入过程是为基于网络的优化任务建模的,而不是用户偏好学习。)
- In contrast to CNSR, our work explicitly models the recursive social diffusion process in the global social network for optimizing the recommendation task. (与CNSR不同,我们的工作明确地模拟了全球社会网络中的递归社会扩散过程,以优化推荐任务。)
- Researchers proposed to generate social sequences based on random walks on user-user and user-item graph, and further leveraged the sequence embedding techniques for social recommendation [11]. This model could better capture the higher-order social network structure. However, the performance heavily relies on the choice of random walk strategy, including switching between user-item graph and user-user graph, and the length of random walk, which is both time-consuming and labor-consuming. (研究人员提出基于用户和用户项图上的随机游动生成社交序列,并进一步利用序列嵌入技术进行社交推荐[11]。该模型能够更好地捕捉高阶社会网络结构。然而,性能在很大程度上取决于随机游走策略的选择,包括在用户项目图和用户用户图之间切换,以及随机游走的长度,这既耗时又费工。)
2.2.2 Graph Convolutional Networks and Applications in Recommendation.
-
(1) GCNs generalize the convolutional operations from the regular Euclidean domains to non-Euclidean graph and have empirically shown great success in graph representation learning [5], [8], [22]. (GCN将卷积运算从正则欧几里德域推广到非欧几里德图,并在图表示学习[5]、[8]、[22]方面取得了巨大的成功。)
-
Specifically, GCNs recursively perform message passing by applying convolutional operations to aggregate the neighborhood information, such that the K-th order graph structure is captured with K iterations [22]. By treating the user-item interaction as a graph structure, GCNs have been applied for recommendation [48], [51]. (具体而言,GCN通过应用卷积运算来聚合邻域信息,从而递归地执行消息传递,从而通过K次迭代捕获K阶图结构[22]。通过将用户项目交互视为一个图形结构,GCN已被应用于建议[48],[51]。)
-
Earlier works relied on spectral GCNs, and suffered from huge time complexity [33], [51]. Therefore, many recent works focus on the spatial based GCNs for recommendation [48], [4], [49], [41]. (早期的工作依赖于光谱GCN,并且具有巨大的时间复杂性[33],[51]。因此,最近的许多工作都集中在基于空间的GCN推荐上)
- PinSage is a GCN based content recommendation model by propagating item features in the item-item correlation graph [48]. (PinSage是一种基于GCN的内容推荐模型,通过在项目关联图中传播项目特征)
- GCMC applied graph neural network for CF, with the first order neighborhood is directly modeled in the process [4]. (GCMC应用于CF的图形神经网络,在该过程中直接对一阶邻域进行建模)
- NGCF extended GC-MC with multiple layers, such that the higher-order collaborative signals between users and items can be modeled in the user and item embedding learning process [41]. (NGCF对GC-MC进行了多层扩展,使得用户和项目之间的高阶协作信号可以在用户和项目嵌入学习过程中建模)
-
(2) As the social structure among users could be naturally formulated as a user-user graph, recently we propose a preliminary graph based social recommendation model, DiffNet, for modeling the social diffusion process in recommendation [43]. DiffNet advances classical embedding based models with carefully designed influence diffusion layers, such that how users are influenced by the recursive influence diffusion process in the social network could be well modeled. (由于用户之间的社会结构可以自然地表示为用户-用户图,最近我们提出了一个初步的基于图的社会推荐模型DiffNet,用于在推荐中建模社会扩散过程[43]。DiffNet提出了经典的基于嵌入的模型,并精心设计了影响扩散层,从而可以很好地模拟社交网络中递归影响扩散过程对用户的影响。)
- Given each user a a a, the user embedding u a u_a ua is sent to the influence diffusion layers. (给定每个用户 a a a,嵌入 u a u_a ua的用户 被发送到影响扩散层。)
- Specifically, let K K K denote the depth of the influence diffusion layers and h a k h^k_a hak is the user representation at the k k k-th layer of the influence diffusion part. (具体地说,让 K K K表示影响扩散层的深度和 h a k h^k_a hak是影响扩散部分第 k k k层的用户表示。)
- For each user a a a, her updated embedding h a k + 1 h^{k+1}_a hak+1 is performed by social diffusion of the embeddings at the k k k-th layer with two steps: (对于每个用户 a a a,他更新的嵌入 h a k + 1 h^{k+1}_a hak+1通过 k k k层嵌入物的社会扩散,分两步进行:)
- aggregation from her social neighbors at the k k k-th layer (Eq.(4)), (他在第 k k k层的社交邻居聚集在一起)
- and combination of her own latent embedding h a k h^k_a hak at k k k-th layer and neighbors:
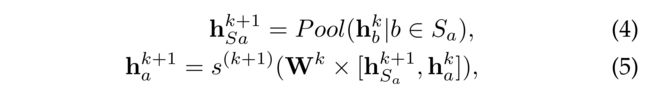
- where the first equation is a pooling operation that transforms all the social trusted users’ influences into a fixed length vector h S a k + 1 h^{k+1}_{S_a} hSak+1, s ( x ) s(x) s(x) is a transformation function and we use s ( k + 1 ) s^{(k+1)} s(k+1) to denote the transformation function for ( k + 1 ) (k+1) (k+1)-th layer.
- As such, with a diffusion depth K K K, DiffNet could automatically models how users are influenced by the K K K-th order social neighbors in a social network for social recommendation. When K K K = 0, the social diffusion layers disappear and DiffNet degenerates to classical CF models. (因此,通过扩散深度 K K K,DiffNet可以自动建模用户如何受到社交网络中第 K K K阶社交邻居的影响,以进行社交推荐。当 K K K=0时,社会扩散层消失,DiffNet退化为经典的CF模型。)
-
(3) In summary , all these previous GCN based models either considered the higher-order social network or the higher-order user interest network for recommendation. (综上所述,之前所有这些基于GCN的模型要么考虑高阶社交网络,要么考虑高阶用户兴趣网络进行推荐。)
-
There are some recently works that also leverage the graph neural networks for social recommendation [10], [45]. Specifically, (最近有一些研究也利用图形神经网络进行社会推荐[10],[45]。明确地)
- GraphRec is designed to learn user representations by fusing first order social and first-order item neighbors with non-linear neural networks [10]. (GraphRec旨在通过将一阶社交和一阶项目邻居与非线性神经网络融合来学习用户表示[10]。)
- Researchers also proposed deep learning techniques to model the complex interaction of dynamic and static patterns reflected from users’ social behavior and item preferences [45]. (研究人员还提出了深度学习技术,以模拟用户社会行为和项目偏好所反映的动态和静态模式的复杂交互[45]。)
- Although these works relied on deep learning based models with users’ two kinds of behaviors, they only modeled the first order structure of the social graph and interest graph. We differ from these works as we simultaneously fuse the higher-order social and interest network structure for better social recommendation. (尽管这些工作依赖于基于深度学习的模型,对用户的两种行为进行建模,但它们只对社交图和兴趣图的一阶结构进行建模。我们不同于这些作品,因为我们同时融合了高阶社会和兴趣网络结构,以获得更好的社会推荐。)
2.2.3 Attention Models and Applications.
- (1) As a powerful and common technique, attention mechanism is often adopted when multiple elements in a sequence or set would have an impact of the following output, such that attentive weights are learned with deep neural networks to distinguish important elements [18], [3], [46]. (作为一种强大而常见的技术,当一个序列或集合中的多个元素会对后续输出产生影响时,通常会采用注意机制,例如,使用深层神经网络学习注意权重,以区分重要元素[18],[3],[46]。)
- Given a user’s rated item history , NAIS is proposed to learn the neural attentive weights for item similarity in item based collaborative filtering [16]. (考虑到用户的评分项目历史,建议NAIS学习基于项目的协同过滤中项目相似性的神经注意权重[16]。)
- For graph structure data, researchers proposed graph attention networks to attentively learn weights of each neighbor node in the graph convolutional process [40]. (对于图结构数据,研究人员提出图注意网络,以便在图卷积过程中仔细学习每个相邻节点的权重[40]。)
- In social recommendation, many attention models have been proposed to learn the social influence strength [35], [38], [13], [10]. E.g., (在社会推荐中,人们提出了许多注意模型来学习社会影响力强度[35]、[38]、[13]、[10]。例如。,)
- with each user’s direct item neighbors and social neighbors, GraphRec leverages attention modeling to learn the attentive weights for each social neighbor and each rated item for user modeling [10]. (对于每个用户的直接项目邻居和社交邻居,GraphRec利用注意力建模来了解每个社交邻居和每个用户建模评分项目的注意力权重[10]。)
- In social contextual recommender systems , users’ preferences are influenced by various social contextual aspect, and an attention network was proposed to learn the attention weight of each social contextual aspect in the user decision process. (在社会语境推荐系统中,用户的偏好受到各种社会语境因素的影响,提出了一个注意网络来学习用户决策过程中各个社会语境因素的注意权重。)
- Our work is also inspired by the applications of attention modeling, and apply it to fuse the social network and interest network for social recommendation. (我们的工作也受到了注意力建模应用的启发,并将其应用于融合社交网络和兴趣网络进行社会推荐。)
3 THE PROPOSED MODEL
- In this section, we first show the overall architecture of our proposed model DiffNet++, followed by each component. After that, we will introduce the learning process of DiffNet++. Finally, we give a detailed discussion of the proposed model. (在本节中,我们首先展示我们提出的DiffNet++模型的总体架构,然后是每个组件。之后,我们将介绍DiffNet++的学习过程。最后,我们对所提出的模型进行了详细的讨论。)
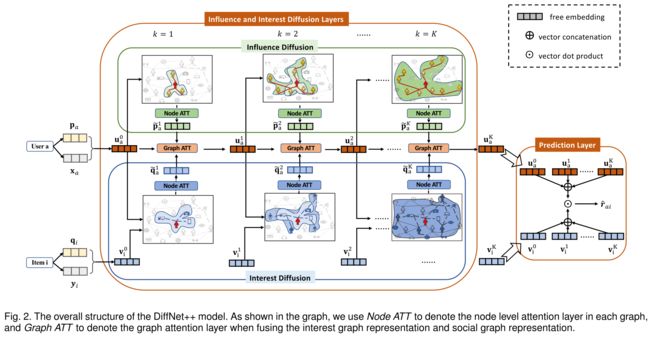
3.1 Model Architecture
- (1) As shown in the related work part, our preliminary work of DiffNet adopts the recursive influence diffusion process for iterative user embedding learning, such that the up to K K K-th order social network structure is injected into the social recommendation process [43]. (如相关工作部分所示,DiffNet的前期工作采用递归影响扩散过程进行迭代用户嵌入学习,从而将高达 K K K阶的社交网络结构注入到社交推荐过程中[43]。)
- In this part, we propose DiffNet++, an enhanced model of DiffNet that fuses both influence diffusion in the social network G S G_S GS and interest diffusion in the interest network G I G_I GI for social recommendation. (在这一部分中,我们提出了DiffNet++,这是一个增强的DiffNet模型,它融合了社交网络 G S G_S GS中的影响扩散以及兴趣网络 G I G_I GI中的兴趣扩散去社会推荐。)
- We show the overall neural architecture of DiffNet++ in Fig. 2. The architecture of DiffNet++ contains four main parts:
- an embedding layer, (一个嵌入层,)
- a fusion layer, (融合层,)
- the influence and interest diffusion layers, (影响和兴趣扩散层,)
- and a rating prediction layer. (评级预测层。)
- Specifically, by taking related inputs,
- the embedding layer outputs free embeddings of users and items, (嵌入层输出用户和项目的自由嵌入,)
- and the fusion layer fuses both the content features and free embeddings. (融合层融合了内容特征和免费嵌入。)
- In the influence and interest diffusion layers, we carefully design a multi-level attention structure that could effectively diffuse higher-order social and interest networks. (在影响和兴趣扩散层,我们精心设计了一个多层次的注意结构,可以有效地扩散高阶社会和兴趣网络。)
- After the diffusion process reaches stable, the output layer predicts the preference score of each unobserved user-item pair. (在扩散过程达到稳定后,输出层预测每个未观察到的用户项对的偏好分数。)
3.1.1 Embedding Layer.
- (1) It encodes users and items with corresponding free vector representations. Let P ∈ R M × D P \in R^{M\times D} P∈RM×D and Q ∈ R N × D Q \in R^{N\times D} Q∈RN×D represent the free latent embedding matrices of users and items with D D D dimensions.
- Given the one hot representations of user a a a, the embedding layer performs an index selection and outputs the free user latent embedding p a p_a pa, i.e., the transpose of a a a-th row from user free embedding matrix P P P. (给定用户 a a a的one-hot表示,嵌入层执行索引选择并输出自由用户潜在嵌入 p a pa pa,即从用户自由嵌入矩阵 P P P转置第 a a a行。)
- Similarly , item i’s embedding q i qi qi is the transpose of i i i-th row of item free embedding matrix Q Q Q. (同样,项目 i i i的嵌入 q i q_i qi是项目自由嵌入矩阵 Q Q Q第 i i i行的转置。)
3.1.2 Fusion Layer.
-
(1) For each user a a a, the fusion layer takes p a p_a pa and her associated feature vector x a x_a xa as input, and outputs a user fusion embedding u a 0 u^0_a ua0 that captures the user’s initial interests from different kinds of input data. We model the fusion layer as: (对于每个用户 a a a,融合层将 p a p_a pa及其关联的特征向量 x a x_a xa作为输入,并输出用户融合嵌入 u a 0 u^0_a ua0,从不同类型的输入数据中捕获用户的初始兴趣。我们将融合层建模为:)

- where W 1 W_1 W1 is a transformation matrix,
- and g ( x ) g(x) g(x) is a transformation function.
- Without confusion, we omit the bias term. This fusion layer could generalize many typical fusion operations, such as the concatenation operation u a 0 = [ p a , x a ] u^0_a = [p_a, x_a] ua0=[pa,xa] by setting W 1 W_1 W1 as an identity matrix and g ( x ) g(x) g(x) an identity function.
-
(2) Similarly , for each item i i i, the fusion layer models the item embedding v i 0 v^0_i vi0 as a function between its free latent vector q i q_i qi and its feature vector y i y_i yi as: (类似地,对于每个项目 i i i,融合层对嵌入 v i 0 v^0_i vi0的项目进行建模作为自由潜向量 q i q_i qi及其特征向量 y i y_i yi之间的函数)

3.1.3 Influence and Interest Diffusion Layers.
-
(1) By feeding the output of each user a’s fused embedding u a 0 u^0_a ua0 and each item i i i’s fused embedding v i 0 v^0_i vi0 into the influence and interest diffusion layers, these layers recursively model the dynamics of this user’s latent preference and the item’s latent preference propagation in the graph G G G with layer-wise convolutions. (通过输入每个用户 a a a的融合嵌入 u a 0 u^0_a ua0的输出以及每一项 i i i的融合嵌入 v i 0 v^0_i vi0在影响层和兴趣扩散层中,在图 G G G中这些层使用分层卷积递归地建模该用户的潜在偏好和项目的潜在偏好传播的动力学。)
- In detail, at each layer k + 1 k + 1 k+1, by taking user a a a’s embedding u a k u^k_a uak and item i i i’s embedding v i k v^k_i vik from previous layer k k k as input, these layers recursively output the updated embeddings of v i k + 1 v^{k+1}_i vik+1 and u a k + 1 u^{k+1}_a uak+1 with diffusion operations.
- This iteration step starts at k = 0 k = 0 k=0 and stops when the recursive process reaches a pre-defined depth K K K. (该迭代步骤从 k = 0 k=0 k=0开始,当递归过程达到预定义深度 K K K时停止。)
- As each item only appears in the user-item interest graph G I G_I GI, in the following, we would first introduce how to update item embeddings, followed by the user embedding with influence and interest diffusions. (由于每个项目仅出现在用户项目兴趣图 G I G_I GI中 , 在下文中,我们将首先介绍如何更新项目嵌入,然后介绍具有影响力和兴趣扩散的用户嵌入。)
-
(2) For each item i i i, given its k k k-th layer embedding v i k v^k_i vik, we model the updated item embedding v i k + 1 v^{k+1}_i vik+1 at the ( k + 1 ) (k+1) (k+1)-th layer from G I G_I GI as:

- where R i = [ a ∣ r i a = 1 ] R_i = [a | r_{ia} = 1] Ri=[a∣ria=1] is the userset that rates item i i i. (对项目ii进行评分的用户集。)
- u a k u^k_a uak is the k k k-th layer embedding of user a a a. (用户 a a a的第 k k k层嵌入。)
- v ^ i k + 1 \hat{v}^{k+1}_i v^ik+1 is the item i i i’s aggregated embedding from its neighbor users in the user-item interest graph G I G_I GI, (是在用户项兴趣图 G I G_I GI中,项 i i i从其相邻用户的聚合嵌入,)
- with η i a k + 1 \eta^{k+1}_{ia} ηiak+1 denotes the aggregation weight. (表示聚合权重。)
- After obtaining the aggregated embedding v ^ i k + 1 \hat{v}^{k+1}_i v^ik+1 from the k k k-th layer, each item’s updated embedding v i k + 1 v^{k+1}_i vik+1 is a fusion of the aggregated neighbors’ embeddings and the item’s emebedding at previous layer k k k. (从第 k k k层获得聚合嵌入 v ^ i k + 1 \hat{v}^{k+1}_i v^ik+1之后,每个项目的更新嵌入 v i k + 1 v^{k+1}_i vik+1是聚合的邻居的嵌入和前一层 k k k中项目的嵌入的融合。)
- In fact, we try different kinds of fusion functions, including the concatenation and the addition, and find the addition always shows the best performance. Therefore, we use the addition as the fusion function in Eq.(9). (事实上,我们尝试了不同类型的融合函数,包括级联和加法,发现加法总是表现出最好的性能。因此,我们使用加法作为等式(9)中的融合函数。)
-
(3) In the item neighbor aggregation function, Eq.(8) shows the weight of user a a a to item i i i. A naive idea is to aggregate the embeddings from i i i’s neighbor users with mean pooling operation, i.e., v ^ i k + 1 = ∑ a ∈ R i 1 ∣ R i ∣ u a k \hat{v}^{k+1}_i = \sum_{a\in R_i} \frac{1} {|Ri|} u^k_a v^ik+1=∑a∈Ri∣Ri∣1uak. However, it neglects the different interest weights from users, as the importance values of different users vary in item representation. Therefore, we use an attention network to learn the attentive weight η i a k + 1 \eta^{k+1}_{ia} ηiak+1 in Eq.(8) as: (然而,由于不同用户在项目表示中的重要性值不同,它忽略了用户的不同兴趣权重。因此,我们使用注意网络来学习注意权重 η i a k + 1 \eta^{k+1}_{ia} ηiak+1在等式(8)中,如下所示:)
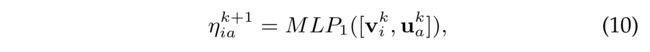
- where a MultiLayer Perceptrion (MLP) is used to learn the node attention weights with the related user and item embeddings at the k k k-th layer. After that, we normalize the attention weights with: (其中,多层感知器(MLP)用于学习节点注意权重,相关用户和项目嵌入在第 k k k层。之后,我们用以下方法将注意力权重标准化:)

- Specifically, the exponential function is used to ensure each attention weight is larger than 0. (具体来说,指数函数用于确保每个注意权重大于0。)
- where a MultiLayer Perceptrion (MLP) is used to learn the node attention weights with the related user and item embeddings at the k k k-th layer. After that, we normalize the attention weights with: (其中,多层感知器(MLP)用于学习节点注意权重,相关用户和项目嵌入在第 k k k层。之后,我们用以下方法将注意力权重标准化:)
-
(4) For each user a a a, let u a k u^k_a uak denote her latent embedding at the k k k-th layer. As users play a central role in both the social network GSand the interest network G I G_I GI, besides her own latent embedding u a k u^k_a uak, her updated embedding u a ( k + 1 ) u^{(k+1)}_a ua(k+1) at ( k + 1 ) (k + 1) (k+1)-th layer is influenced by two graphs:
- the influence diffusion in G S G_S GS
- and the interest diffusion in G I G_I GI.
- Let p ^ a k + 1 \hat{p}^{k+1}_a p^ak+1 denote the aggregated embedding of influence diffusion from the social neighbors
- and q ^ a k + 1 \hat{q}^{k+1}_a q^ak+1 represents the embedding of aggregated interest diffusion from the interested item neighbors at the ( k + 1 ) (k + 1) (k+1)-th layer. Then, each user’s updated embedding u a k + 1 u^{k+1}_a uak+1 is modeled as:

- where Eq.(12) shows how each user updates her latent embedding by fusing the influence diffusion aggregation p ^ a k + 1 \hat{p}^{k+1}_a p^ak+1 and interest diffusion aggregation q ^ a k + 1 \hat{q}^{k+1}_a q^ak+1, as well as her own embedding u a k u^k_a uak at previous layer.
- Since each user appears in both the social graph and interest graph, Eq.(13) and Eq.(14) model the influence diffusion aggregation and interest diffusion aggregation from the two graphs respectively. (由于每个用户都出现在社交图和兴趣图中,因此等式(13)和等式(14)分别对来自这两个图的影响扩散聚合和兴趣扩散聚合进行建模。)
- Specifically, α a b k + 1 \alpha^{k+1}_{ab} αabk+1 denotes the social influence of user b b b to a a a at the ( k + 1 ) (k + 1) (k+1)-th layer in the social network, and β a i k + 1 \beta^{k+1}_{ai} βaik+1 denotes the attraction of item i i i to user a a a at the ( k + 1 ) (k + 1) (k+1)-th layer in the interest network.
-
(5) In addition to the user and item embeddings, there are three groups of weights in the above three equations. A naive idea is to directly et equal values of each kind of weights, i.e., γ a 1 ( k + 1 ) = γ a 2 ( k + 1 ) = 1 2 , α a b ( k + 1 ) = 1 ∣ S a ∣ \gamma^{(k+1)}_{a1} = \gamma^{(k+1)}_{a2} = \frac{1}{2}, \alpha^{(k+1)}_{ab} = \frac{1}{|Sa|} γa1(k+1)=γa2(k+1)=21,αab(k+1)=∣Sa∣1, and β ( k + 1 ) a i = 1 ∣ R a ∣ β(k+1) ai = 1 |Ra| β(k+1)ai=1∣Ra∣. (除了用户和项目嵌入,上述三个等式中还有三组权重。一个天真的想法是直接将每种权重的值相等)
-
However, this simple idea could not well model the different kinds of weights in the user decision process. In fact, these three groups of weights naturally present a two-layer multi-level structure. (然而,这种简单的想法无法很好地模拟用户决策过程中的各种权重。事实上,这三组权重自然呈现出两层多层次的结构。)
-
Specifically, the social influence strengths and the interest strengths could be seen as node-level weights, which model how each user balances different neighboring nodes in each graph.
-
By sending the aggregations of node level attention into Eq.(12), γ a l k + 1 \gamma^{k+1}_{al} γalk+1 is the graph level weight that learns to fuse and aggregate information from different graphs. Specifically, the graph layer weights are important as they model how each user balances the social influences and her historical records for user embedding. Different users vary, with some users are more likely to be swayed by the social network while the interests of others are quite stable. Therefore, the weights in the graph attention layer for each user also need to be personally adapted. (通过将节点级注意力的聚集发送到等式(12), γ a l k + 1 \gamma ^{k+1}_{al} γalk+1是学习融合和聚合来自不同图形的信息的图形级权重。具体来说,图层权重很重要,因为它们模拟了每个用户如何平衡社会影响和用户嵌入的历史记录。不同的用户各不相同,一些用户更容易受到社交网络的影响,而另一些用户的兴趣则相当稳定。因此,每个用户在图形注意层中的权重也需要进行个人调整。)
-
(6) As the three groups of weights represent a multi-level structure, we therefore use a multi-level attention network to model the attentive weights. (由于这三组权重代表一个多层次的结构,因此我们使用一个多层次的注意网络来建模注意权重。)
-
Specifically, the graph attention network is designed to learn the contribution weight of each aspect when updating a’s embedding with different graphs, i.e., p ^ a k + 1 \hat{p}^{k+1}_a p^ak+1 and q ^ a k + 1 \hat{q}^{k+1}_a q^ak+1 in Eq.(12), (具体来说,图注意网络的设计是为了在用不同的图更新a的嵌入时,了解每个方面的贡献权重,)
-
and the node attention networks are designed to learn the attentive weights in each social graph and each interest graph respectively . Specifically, the social influence score α a b k + 1 α^{k+1}_{ab} αabk+1 is calculated as follows: (节点注意网络分别用于学习每个社会图和每个兴趣图中的注意权重。具体来说,社会影响评分 α a b k + 1 α^{k+1}_{ab} αabk+1计算方法如下)

-
(7) In the above equation, the social influence strength α a b k + 1 \alpha^{k+1}_{ab} αabk+1 takes the related two users’ embeddings at the k k k-th layer as input, and sending these features into a MLP to learn the complex relationship between features for social influence strength learning. Without confusion, we omit the normalization step of all attention modeling in the following, as all of them share the similar form as shown in Eq.(11). (在上述等式中,社会影响强度 α a b k + 1 \alpha^{k+1}_{ab} αabk+1将相关的两个用户在 k k k-th层的嵌入作为输入,并将这些特征发送到MLP中,以了解特征之间的复杂关系,从而进行社会影响强度学习。毫无疑问,我们在下文中省略了所有注意力建模的规范化步骤,因为它们都具有类似的形式,如等式(11)所示。)
-
(8) Similarly, we calculate the interest influence score β a i k + 1 \beta^{k+1}_{ai} βaik+1 by taking related user embedding and item embedding as input: (同样,我们计算利息影响分数 β a i k + 1 \beta^{k+1}_{ai} βaik+1以相关用户嵌入和项目嵌入为输入:)

-
(9) After obtaining the two groups of the node attentive weights, the output of the node attention weights are sent to the graph attention network, and we could model the graph attention weights of γ a l k + 1 \gamma^{k+1}_{al} γalk+1 ( l l l = 1,2) as: (在获得两组节点注意权值后,将节点注意权值的输出发送到图注意网络,我们可以对节点的图注意权值进行建模)

-
(10) In the above equation, for each user a a a, the graph attention layer scores not only rely on the user’s embedding ( u a k ) (u^k_a) (uak), but also the weighted representations that are learnt from the node attention network. (在上面的等式中,对于每个用户 a a a,图注意层分数不仅取决于用户的嵌入( u a k u^k_a uak), 还包括从节点注意网络中学习到的加权表示。)
-
(11) For example, as shown in Eq.(12), γ a 1 ( k + 1 ) \gamma^{(k+1)}_{a1} γa1(k+1) denotes the influence diffusion weight for contributing to users’ depth ( k + 1 ) (k + 1) (k+1) embedding , with additional input of the learned attentive combination of the influence diffusion aggregation in Eq.(13). (表示有助于用户深度 ( k + 1 ) (k+1) (k+1)嵌入的影响扩散权重,并额外输入公式(13)中学习到的影响扩散聚合的注意组合。)
- Similarly, γ a 2 ( k + 1 ) \gamma^{(k+1)} _{a2} γa2(k+1) denotes the interest diffusion weight for contributing to users’ depth ( k + 1 ) (k+1) (k+1) embedding , with additional input of the learned attentive combination of the interest diffusion aggregation in Eq.(14). (表示有助于用户深度 ( k + 1 ) (k+1) (k+1)嵌入的兴趣扩散权重,以及公式(14)中学习到的兴趣扩散聚合的注意组合的额外输入。)
- As γ a 1 k + 1 + γ a 2 k + 1 = 1 γ^{k+1}_{a1} + \gamma^{k+1}_{a2} = 1 γa1k+1+γa2k+1=1, larger γ a 1 k + 1 \gamma^{k+1}_{a1} γa1k+1 denotes higher influence diffusion effect with less interest diffusion effect. (表示影响扩散效应越大,兴趣扩散效应越小。)
- Therefore, the learned aspect importance scores are tailored to each user, which distinguish the importance of the influence diffusion effect and interest diffusion effect during the user’s embedding updating process. (因此,学习的方面重要性分数是针对每个用户定制的,这区分了用户嵌入更新过程中影响扩散效应和兴趣扩散效应的重要性。)
3.1.4 Prediction Layer.
- (1) After the iterative K K K-layer diffusion process, we obtain the embedding set of u u u and i i i with u a k u^k_a uak and v i k v^k_i vik for k = [ 0 , 1 , 2 , . . . , K ] k = [0,1,2, ..., K] k=[0,1,2,...,K]. (经过迭代 K K K层扩散过程,我们得到了 u u u和 i i i的嵌入集)
- Then, for each user a a a, her final embedding is denoted as: u a ∗ = [ u a 0 ∣ ∣ u a 1 ∣ ∣ . . . ∣ ∣ u a K ] u^∗_a= [u^0_a || u^1_a || ... || u^K_a] ua∗=[ua0∣∣ua1∣∣...∣∣uaK] that concatenates her embedding at each layer.
- Similarly , each item i i i’s final embedding is : v i ∗ = [ v i 0 ∣ ∣ v i 1 ∣ ∣ . . . ∣ ∣ v i K ] v^∗_i= [v^0_i || v^1_i || ... || v^K_i] vi∗=[vi0∣∣vi1∣∣...∣∣viK].
- After that, the predicted rating is modeled as the inner product between the final user and item embeddings [7]: (之后,预测评级被建模为最终用户和项目嵌入之间的内积[7]:)

- (2) Please note that, some previous works directly use the K K K-th layer embedding for prediction layer as r ^ a i = [ u a K ] T V i K . \hat{r}_{ai} = [u^K_a]^T V^K_ i. r^ai=[uaK]TViK. (请注意,以前的一些工作直接使用 K K K-th层嵌入作为预测层)
- Recently , researchers found that if we use the K-th layer embedding, GCN based approaches are proven to over-smoothing issue as K increases [27], [52]. (最近,研究人员发现,如果我们使用第K层嵌入,基于GCN的方法被证明会随着K的增加而过度平滑[27],[52]。)
- In this paper, to tackle the over-smoothing problem, we adopt the prediction layer as the LR-GCCF model, which receives state-of-the-art performance with user-item bipartite graph structure [7]. (在本文中,为了解决过度平滑问题,我们采用预测层作为LR-GCCF模型,该模型采用用户项二部图结构[7]获得最先进的性能。)
- In LR-GCCF, Chen et al. carefully analyzed the simple concatenation of entity embedding at each layer is equivalent to residual preference learning, and why this simple operation could alleviate the over-smoothing issue [7]. (在LR-GCCF中,Chen等人仔细分析了实体嵌入在每一层的简单串联相当于残差偏好学习,以及为什么这种简单操作可以缓解过度平滑问题[7]。)
3.2 Model Training
-
(1) We use a pair-wise ranking based loss function for optimization, which is widely used for implicit feedback [37]: (我们使用基于成对排序的损失函数进行优化,该函数广泛用于隐式反馈[37]:)

- where R + R^+ R+ denotes the set of positive samples (observed user-item pairs),
- and R − R^− R− denotes the set of negative samples (unobserved user-item pairs that randomly sampled from R).
- σ ( x ) \sigma(x) σ(x) is sigmoid function.
- Θ = [ Θ 1 , Θ 2 ] \Theta = [\Theta_1, \Theta_2] Θ=[Θ1,Θ2] is the regularization parameters in our model,
- with Θ 1 = [ P , Q ] \Theta_1 = [P, Q] Θ1=[P,Q], and the parameter set in the fusion layer and the multi-level attention modeling, i.e.,
- Θ 2 = [ W 1 , W 2 , [ M L P i ] i = 1 , 2 , 3 , 4 ] \Theta_2= [W_1, W_2, [MLP_i]_{i=1,2,3,4}] Θ2=[W1,W2,[MLPi]i=1,2,3,4].
- All the parameters in the above loss function are differentiable.
-
(2) For all the trainable parameters, we initialize them with the Gaussian distribution with a mean value of 0 and a standard deviation of 0.01.
- Besides, we do not deliberately adjust the dimensions of each embedding size in the convolutional layer, all of them keep the same size.
- As for the several MLPs in the multi-level attention network, we use two-layer structure.
- In the experiment part, we will give more detail descriptions about the parameter setting. (在实验部分,我们将对参数设置进行更详细的描述。)
3.3 Matrix Formulation of DiffNet++
-
(1) The key idea of our proposed DiffNet++ model is the well designed interest and influence diffusion layers. In fact, this part could be calculated in matrix forms. In the following, we would like to show how to update user and item embedding from the k-th layer to the (k + 1)-th layer with matrix operations. Let H ( k + 1 ) = [ η i a k + 1 ] ∈ R N × M H^{(k+1)} = [\eta^{k+1}_{ia}] \in R^{N\times M} H(k+1)=[ηiak+1]∈RN×M denote the matrix representation of attentive item aggregation weigth in Eq.(10), we have: (我们提出的DiffNet++模型的关键思想是精心设计的兴趣和影响扩散层。事实上,这一部分可以用矩阵形式计算。在下面,我们将展示如何使用矩阵运算将用户和项目嵌入从第k层更新到(k+1)层。设 H ( k + 1 ) = [ η i a k + 1 ] ∈ R N × M H^{(k+1)} = [\eta^{k+1}_{ia}] \in R^{N\times M} H(k+1)=[ηiak+1]∈RN×M表示式(10)中注意事项聚合权重的矩阵表示,我们有:)
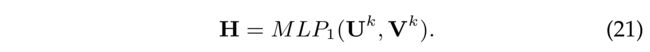
-
(2) At the user side, given Eq.(12) ,
- let A ( k + 1 ) = [ α a b k + 1 ] ∈ R M × M A^{(k+1)} = [\alpha^{k+1}_{ab}] \in R^{M\times M} A(k+1)=[αabk+1]∈RM×M,
- B ( k + 1 ) = [ β i a k + 1 ] ∈ R M × N B^{(k+1)} = [\beta^{k+1}_{ia}] \in R^{M\times N} B(k+1)=[βiak+1]∈RM×N denote the attentive weight matrices of social network (Eq.(13)) and interest network(Eq.(14)), i.e., the outputs of the node attention layer. (表示社交网络(等式(13))和兴趣网络(等式(14))的关注权重矩阵,即节点关注层的输出。)
- We use Γ ( k + 1 ) = [ γ a l k + 1 ] ∈ R M × 2 \Gamma^{(k+1)} = [\gamma^{k+1}_{al}] \in R^{M\times 2} Γ(k+1)=[γalk+1]∈RM×2 to denote the attentive weight matrix of the multi-level networks in Eq.(17) and Eq.(18). All these three attention matrices can be calculated similarly as shown above. (表示式(17)和式(18)中多级网络 的 注意权重矩阵。所有这三个注意矩阵的计算方法都可以类似地如上所示。)
-
(3) After learning the attention matrices, we could update user and item embeddings at the (k + 1)-th layer as: (在学习了注意矩阵之后,我们可以将(k+1)层的用户和项目嵌入更新为:)
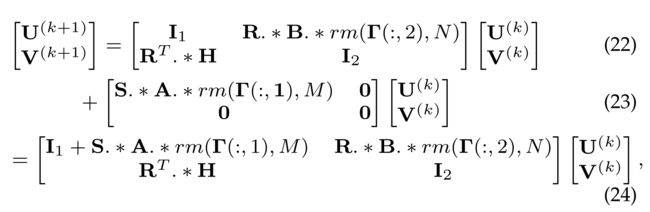
- where I 1 I_1 I1 is an identity matrix with M M M rows,
- and I 2 I_2 I2 is an identity matrix with N N N rows.
- Moreover, Γ ( : , 1 ) \Gamma(:,1) Γ(:,1) and Γ ( : , 2 ) \Gamma(:,2) Γ(:,2) represent the first column and second column of matrix Γ \Gamma Γ, . (表示矩阵 Γ \Gamma Γ的第一列和第二列。)
- ∗ ∗ ∗ denotes the dot product and r m ( A , r 1 ) rm(A, r_1) rm(A,r1) denotes an array that containing r 1 r_1 r1 copies of A A A in the column dimensions. (∗ 表示点积和 r m ( A , r 1 ) rm(A,r_1) rm(A,r1)表示包含 r 1 r_1 r1的数组 A A A在尺寸栏中的副本)
-
(4) Based on the above matrix operations of the social and influence diffusion layers, DiffNet++ is easily implemented by current deep learning frameworks. (基于上述社交和影响扩散层的矩阵运算,DiffNet++很容易通过当前的深度学习框架实现。)
3.4 Discussion
3.4.1 Space complexity.
- As shown in Eq.(20), the model parameters are composed of two parts:
- the user and item free embeddings Θ 1 = [ P , Q ] \Theta_1=[P, Q] Θ1=[P,Q], (用户和项目自由嵌入)
- and the parameter set in the fusion layer and the attention modeling, i.e., Θ 2 = [ W 1 , W 2 , [ M L P i ] i = 1 , 2 , 3 , 4 ] \Theta_2 = [W_1, W_2, [MLP_i]_{i=1,2,3,4}] Θ2=[W1,W2,[MLPi]i=1,2,3,4]. (融合层参数设置与注意建模)
- Since most embedding based models (e.g., BPR [37], FM [36]) need to store the embeddings of each user and each item, (由于大多数基于嵌入的模型(例如BPR[37],FM[36])需要存储每个用户和每个项目的嵌入,)
- the space complexity of Θ 1 \Theta_1 Θ1 is the same as classical embedding based models and grows linearly with users and items. ( Θ 1 \Theta_1 Θ1的空间复杂性与经典的基于嵌入的模型相同,并随用户和项目线性增长)
- For parameters in Θ 2 \Theta_2 Θ2, they are shared among all users and items, with the dimension of each parameter is far less than the number of users and items. (对于 Θ 2 \Theta_2 Θ2中的参数,它们在所有用户和项目之间共享,每个参数的维度远小于用户和项目的数量。)
- In practice, we empirically find the two-layer MLP achieve the best performance. (在实践中,我们经验发现两层MLP实现了最佳性能。)
- As such, this additional storage cost is a small constant that could be neglected. Therefore, the space complexity of DiffNet++ is the same as classical embedding models. (因此,这种额外的存储成本是一个可以忽略的小常数。因此,DiffNet++的空间复杂度与经典嵌入模型相同。)
3.4.2 Time complexity.
- Compared to the classical matrix factorization based models, the additional time cost lies in the influence and interest diffusion layers. (与经典的基于矩阵分解的模型相比,额外的时间成本在于影响层和利益扩散层。)
- Given M M M users, N N N items and diffusion depth K K K, suppose each user directly connects to L s L_s Ls users and L i L_i Li items on average, and each item directly connects to L u L_u Lu users.
- At each influence and interest diffusion layer, we need to first calculate the two-level attention weight matrices as shown in Eq.(21), and then update user and item embeddings.
- Since in practice, MLP layers are very small (e.g., two layers), the time cost for attention modeling is about O ( M ( L s + L i ) D + N L u D ) O(M(L_s + L_i)D + N L_u D) O(M(Ls+Li)D+NLuD). After that, as shown in Eq.(24), the user and item update step also costs O ( M ( L s + L i ) D + N L u D ) O(M(L_s+L_i)D+N L_uD) O(M(Ls+Li)D+NLuD).
- Since there are K K K diffusion layers, the total additional time complexity for influence and interest diffusion layers are O ( K ( M ( L s + L i ) + N L u ) D ) O(K(M(L_s + L_i) +N L_u)D) O(K(M(Ls+Li)+NLu)D).
- In practice, as L s , L i , L u ≪ m i n { M , N } L_s, L_i, L_u \ll min\{M, N\} Ls,Li,Lu≪min{M,N}, the additional time is linear with users and items, and grows linearly with
diffusion depth K K K. Therefore, the total time complexity is acceptable in practice.
3.4.3 Model Generalization.
-
(1) The proposed DiffNet++ model is designed under the problem setting with the input of user feature matrix X X X, item feature matrix Y Y Y, and the social network S. (提出的DiffNet++模型是在问题设置下设计的,输入用户特征矩阵 X X X、项目特征矩阵 Y Y Y和社交网络 S S S。)
- Specifically, the fusion layer takes users’ (items’) feature matrix for user (item) representation learning. (具体来说,融合层采用用户(项目)特征矩阵进行用户(项目)表示学习。)
- The layer-wise diffusion layer utilizes the social network structure S S S and the interest network structure R R R to model how users’ latent preferences are dynamically influenced from the recursive influence and interest diffusion process. (分层扩散层利用社会网络结构 S S S和兴趣网络结构 R R R来模拟用户的潜在偏好如何受到递归影响和兴趣扩散过程的动态影响)
- Next, we would show that our proposed model is generally applicable when different kinds of data input are not available. (接下来,我们将证明,当不同类型的数据输入不可用时,我们提出的模型通常是适用的。)
-
(2) When the user (item) features are not available, the fusion layer disappears. In other words, as shown in Eq.(7), each item’s latent embedding v i 0 v^0_i vi0 degenerates to q i q_i qi. (当用户(项目)特征不可用时,融合层消失。换句话说,如等式(7)所示,每个项目的潜在嵌入 v i 0 v^0_i vi0退化为 q i q_i qi .)
- Similarly , each user’s initial layer-0 latent embedding u 0 = p a u^0 = p_a u0=pa (Eq.(6)).
- Similarly , when either the user attributes or the item attributes do not exist, the corresponding fusion layer of user or item degenerates. (同样,当用户属性或项目属性不存在时,相应的用户或项目融合层退化。)
4 EXPERIMENTS
4.0.1 Datasets.
-
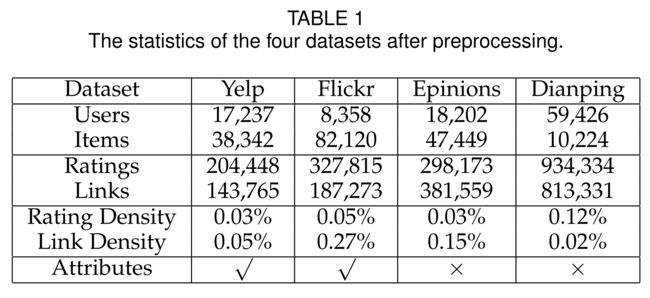
(1) We conduct experiments on four real-world datasets: Yelp, Flickr, Epinions and Dianping. (我们在四个真实数据集上进行了实验:Yelp、Flickr、Epinions和Dianping。)
-
(2) Yelp is a well-known online location based social network, where users could make friends with others and review restaurants. We use the Yelp dataset that is publicly available2. (Yelp是一个著名的基于位置的在线社交网络,用户可以在这里与他人交朋友并查看餐厅。我们使用公开的Yelp数据集2。)
- Flickr3 is an online image based social sharing platform for users to follow others and share image preferences. In this paper, we use the social image recommendation dataset that is crawled and published by authors in [42], with both the social network structure and users’ rating records of images. (Flickr3是一个基于在线图像的社交共享平台,用户可以跟随他人分享图像偏好。在本文中,我们使用了作者在[42]中爬网并发布的社交图像推荐数据集,其中包含了社交网络结构和用户对图像的评分记录。)
- Epinions is a social based product review platform and the dataset is introduced in [31] and is publicly available4. (Epinions是一个基于社交的产品审查平台,数据集在[31]中介绍,并可公开获取4。)
- Dianping is the largest Chinese location based social network, and we use this dataset that is crawled by authors in [26]. This dataset is also publicly available5. (点评是中国最大的基于位置的社交网络,我们使用的是作者在[26]中收集的数据集。该数据集也可公开获取5。)
-
(3) Among the four datasets, Yelp and Flickr are two datasets with user and item attributes, and are adopted as datasets of our previously proposed DiffNet model [43]. (在这四个数据集中,Yelp和Flickr是两个具有用户和项目属性的数据集,它们被用作我们之前提出的DiffNet模型的数据集[43]。)
- The remaining two datasets of Epinions and Dianping do not contain user and item attributes. We use the same preprocessing steps of the four datasets. (Epinions和Dianping的其余两个数据集不包含用户和项目属性。我们对这四个数据集使用相同的预处理步骤。)
- Specifically, as the original ratings are presented with detailed values, we transform the original scores to binary values. (具体来说,由于原始评分以详细值呈现,我们将原始评分转换为二进制值。)
- If the rating value is larger than 3, we transform it into 1, otherwise it equals 0. (如果评级值大于3,我们将其转换为1,否则等于0。)
- For both datasets, we filter out users that have less than 2 rating records and 2 social links and remove items which have been rated less than 2 times. (对于这两个数据集,我们都会筛选出评分记录和社交链接少于2次的用户,并删除评分少于2次的项目)
- We randomly select 10% of the data for the test. In the remaining 90% data, to tune the parameters, we select 10% from the training data as the validation set.
- We show an overview of the characteristics of the four datasets in Table 1. In this table, the last line shows whether the additional user and item attributes are available on this dataset. (我们在表1中概述了这四个数据集的特征。在该表中,最后一行显示了附加的用户和项属性是否在此数据集上可用。)

4.0.2 Baselines and Evaluation Metrics.
- (1) To illustrate the effectiveness of our method, we compare DiffNet++ with competitive baselines, including
- classical CF models (BPR [37], FM [36]),
- social based recommendation model (SocialMF [19], TrustSVD [14], ContextMF [21], CNSR [44]),
- as well as the graph based recommendation models of GraphRec [10], PinSage [48], NGCF [41].
- Please note that, in PinSage, we take the user-item graph with both user and item features as input, in order to transform this model for the recommendation task. (请注意,在PinSage中,我们将包含用户和项目特征的用户项目图作为输入,以便将此模型转换为推荐任务。)
- For our proposed models of DiffNet [43] and DiffNet++, since both models are flexible and could be reduced to simpler versions without user and item features, we use DiffNet-nf and DiffNet+±nf to represent reduced versions of DiffNet and DiffNet++ when removing user and item features. (对于我们提出的DiffNet[43]和DiffNet++模型,由于这两个模型都是灵活的,并且可以简化为没有用户和项目功能的更简单版本,因此在删除用户和项目功能时,我们使用DiffNet nf和DiffNet+±nf来表示DiffNet和DiffNet++的简化版本。)
- For better illustration, we list the main characteristics of all these models in Table 4, with our proposed models are listed with italic letters. (为了更好地说明,我们在表4中列出了所有这些模型的主要特征,我们提出的模型用斜体字母列出。)
- Please note that, as BPR learns free user and item embeddings with the observed user-item ratings. (请注意,随着BPR通过观察到的用户项目评级了解免费用户和项目嵌入。)
- Therefore, the first-order interest network is not learned in the emebedding modeling process. (因此,在建模过程中没有学习到一阶兴趣网络。)
- As can be seen from this paper, our proposed DiffNet+±nf and DiffNet++ are the only two models that consider both the higher-order social influence and higher-order interest network for social recommendation. (从本文中可以看出,我们提出的DIFNET+±NF和DeffNET++是唯一的考虑社会影响的高阶社会影响和高阶兴趣网络的两种模型。)

- (2) For the top-N ranking evaluation, we use two widely used metrics,
- Hit Ratio (HR) [9]
- and Normalized Discounted Cummulative Gain (NDCG) [9], [43].
- Specifically, HR measures the percentage of hit items in the top-N list, (具体来说,HR衡量的是前N名列表中命中项目的百分比,)
- and NDCG puts more emphasis on the top ranked items. (NDCG更注重排名靠前的项目。)
- As we focus on the top-N ranking performance with large itemset, similar as many other works [17], [43], to evaluate the performance, for each user, we randomly select 1000 unrated items that a user has not interacted with as negative samples. (正如许多其他著作[17],[43]一样,我们关注大项目集排名前N的性能,为了评估性能,我们为每个用户随机选择1000个用户未交互的未分级项目作为负样本。)
- Then, we mix these pseudo negative samples and corresponding positive samples (in the test set) to select top-N potential candidates. To reduce the uncertainty in this process, we repeat this procedure 5 times and report the average results. (然后,我们将这些伪阴性样本和相应的阳性样本(在测试集中)混合,以选择前N个潜在候选样本。为了减少这个过程中的不确定性,我们重复这个过程5次,并报告平均结果。)
4.0.3 Parameter Setting.
- For the regularization parameter λ \lambda λ in Eq.(20), we empirically try it in the range of [0.0001, 0.001, 0.01, 0.1] and finally set λ \lambda λ= 0.01 to get the best performance. (对于等式(20)中的正则化参数lambdaλ,我们在[0.0001,0.001,0.01,0.1]范围内进行了经验尝试,最后设置lambdaλ=0.01以获得最佳性能。)
- For the fusion layer in Eq.(6) and Eq.(7), we first transform the each user (item) feature vector to the same free embedding space, and calculate as: u a 0 = W 1 × x a + p a u^0_a = W_1 \times x_a + p_a ua0=W1×xa+pa, and v a 0 = W 2 × y i + q a v^0_a = W_2 \times y_i + q_a va0=W2×yi+qa. (对于式(6)和式(7)中的融合层,我们首先将每个用户(项)特征向量转换为相同的自由嵌入空间,并计算)
- For attention modeling, we resort to MLP with two layers. (对于注意力建模,我们采用两层MLP。)
- For our proposed model, we initialize all of them with a Gaussian distribution with a mean value of 0 and the standard deviation of 0.01. (对于我们提出的模型,我们用均值为0、标准差为0.01的高斯分布初始化所有模型。)
- We use the Adam optimizer for with an initial learning rate of 0.001, and the training batch size is 512. In the training process, as there are much more unobserved items for each user, we randomly select 8 times pseudo negative samples for each user at each iteration. Since each iteration we change the pseudo negative samples, each unobserved item gives very weak signal. (我们使用Adam优化器,初始学习率为0.001,训练批量为512。在训练过程中,由于每个用户有更多未观察到的项目,我们在每次迭代中为每个用户随机选择8次伪阴性样本。由于每次迭代我们都会改变伪负样本,每个未观察到的项目都会给出非常微弱的信号。)
- For all the baselines, we carefully tune the parameters to ensure the best performance. (对于所有基线,我们仔细调整参数以确保最佳性能。)
4.1 Overall Performance Comparison
- (1) We show the overall performance of all models for top-10 recommendation with different embedding size D from Table 3 to Table6. (从表3到表6,我们展示了不同嵌入大小D的top-10推荐的所有模型的总体性能。)
- In Table 3, we show the comparisons on Yelp and Flickr, with the node attribute values are available. (在表3中,我们展示了Yelp和Flickr的比较,节点属性值可用。)
- In Table 4, we depict the results on Epinions and Dianping without attribute values. On Epinions and Dianping, we do not report models that need to take attribute data as input. (在表4中,我们描述了无属性值的Epinions和Dianping的结果。在Epinions和Dianping上,我们不报告需要将属性数据作为输入的模型)
- We notice that besides BPR, nearly all models show better performance with the increase of dimension D D D. All models improve over BPR, which only leverages the observed user-item rating matrix for recommendation, and suffer the data sparsity issue in practice. (我们注意到,除了BPR,几乎所有模型都随着维度DD的增加表现出更好的性能。所有模型都比BPR有所改进,BPR只利用观察到的用户项目评分矩阵进行推荐,并且在实践中存在数据稀疏问题。)
- TrustSVD and SocialMF utilize social neighbors of each user as auxiliary information to alleviate this problem. (TrustSVD和SocialMF利用每个用户的社交邻居作为辅助信息来缓解这个问题。)
- GraphRec further improves over these traditional social recommendation models by jointly considering the first-order social neighbors and interest neighbors in the user embedding process. (GraphRec通过在用户嵌入过程中联合考虑一阶社交邻居和兴趣邻居,进一步改进了这些传统的社交推荐模型。)
- However, GraphRec only models the first-order relationships of two graphs for user embedding learning, with the higher-order graph structures are neglected. (然而,GraphRec仅为用户嵌入学习建模两个图的一阶关系,忽略了高阶图结构。)
- For GCN based models, PinSage and NGCF model the higher-order user-item graph structure, (对于基于GCN的模型,PinSage和NGCF为高阶用户项图结构建模,)
- and DiffNet models the higher-order social structure. (DiffNet为高阶社会结构建模。)
- These graph neural models beat matrix based baselines by a large margin, showing the effectiveness in leveraging higher-order graph structure for recommendation. (这些图神经模型大大超过了基于矩阵的基线,显示了利用高阶图结构进行推荐的有效性。)
- Our proposed DiffNet++ model always performs the best under any dimension D D D, indicating the effectiveness of modeling the recursive diffusion process in the social interest network. (我们提出的DiffNet++模型在任何维度的D下都表现最好,这表明了在社会利益网络中建模递归扩散过程的有效性。)
- Besides, we observe DiffNet++ and DiffNet always show better performance compared to their counterparts that do not model the user and item features, showing the effectiveness of injecting both feature and latent embeddings in the fusion layer. (此外,我们观察到DiffNet++和DiffNet总是比没有对用户和项目特征建模的同类产品表现出更好的性能,显示了在融合层中注入特征和潜在嵌入的有效性。)
- We further compare the performance of different models with different top-N values in Table 5 and Table 6, and the overall trend is the same as analyzed before. Therefore, we could empirically conclude the superiority of our proposed models. As nearly all models showed better performance at D= 64, we would use this setting to show the comparison of different models in the following analysis. (在表5和表6中,我们进一步比较了具有不同top-N值的不同模型的性能,总体趋势与之前分析的相同。因此,我们可以从经验上总结我们提出的模型的优越性。由于几乎所有模型在D=64时都表现出更好的性能,我们将在下面的分析中使用此设置来显示不同模型的比较。)
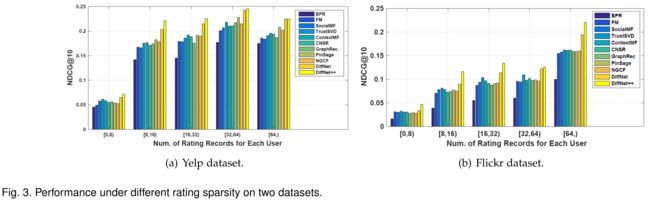
4.2 Performance Under Different Sparsity
- In this part, we would like to investigate how different models perform under different rating sparsity . (在这一部分中,我们将研究不同模型在不同评级稀疏度下的表现。)
- Specifically, we first group users into different interest groups based on the number of observed ratings of each user. E.g, [8,16) means each user has at least 8 rating records and less than 16 rating records. (具体来说,我们首先根据每个用户观察到的评分数将用户分为不同的兴趣组。例如,[8,16]表示每个用户至少有8个评级记录,但少于16个评级记录。)
- Then, we calculate the average performance of each interest group. The sparsity analysis on Yelp dataset and Flickr dataset are shown in Fig. 3(a) and Fig. 3(b) respectively . (然后,我们计算每个利益集团的平均绩效。Yelp数据集和Flickr数据集的稀疏性分析分别如图3(a)和图3(b)所示。)
- From both datasets, we observe that as users have more ratings, the overall performance increases among all models. This is quite reasonable as all models could have more user behavior data for user embedding modeling. (从这两个数据集中,我们观察到,随着用户评分的增加,所有车型的整体性能都会提高。这是非常合理的,因为所有模型都可以有更多的用户行为数据用于用户嵌入建模。)
- Our proposed models consistently improve all baselines, and especially show larger improvements on sparser dataset. E.g., when users have less than 8 rating records, DiffNet++ improves 22.4% and 45.0% over the best baseline on Yelp and Flickr respectively (我们提出的模型持续改进所有基线,尤其是在稀疏数据集上表现出更大的改进。例如,当用户的评分记录少于8次时,DiffNet++在Yelp和Flickr上分别比最佳基线提高了22.4%和45.0%)
4.3 Detailed Model Analysis
4.3.1 Diffusion Depth K.
- The number of layer K is very important, as it determines the diffusion depth of different graphs. We show the results of different K values for two datasets with attributes in Table 7. The column of “Improve” shows the performance changes compared to the best setting, i.e., (K层的数量非常重要,因为它决定了不同图形的扩散深度。我们在表7中展示了两个具有属性的数据集的不同K值的结果。“改进”一栏显示了与最佳设置相比的性能变化,即)
- K = 2. When K increases from 0 to 1, the performance increases quickly (DiffNet++ degenerates to BPR when K = 0), and it achieves the best performance when K = 2. (K=2。当K从0增加到1时,性能迅速提高(当K=0时,DiffNet++退化为BPR),当K=2时,性能达到最佳。)
- However, when we continue to increase the layer to 3, the performance drops. We empirically conclude that 2-hop higher-order social interest graph structure is enough for social recommendation. (但是,当我们继续将层增加到3时,性能会下降。我们的实证结论是,2跳高阶社会兴趣图结构足以满足社会推荐。)
- And adding more layers may introduce unnecessary neighbors in this process, leading to performance decrease. Other related studies have also empirically found similar trends [22], [48]. (在这个过程中,添加更多层可能会引入不必要的邻居,导致性能下降。其他相关研究也在经验上发现了类似的趋势[22],[48]。)

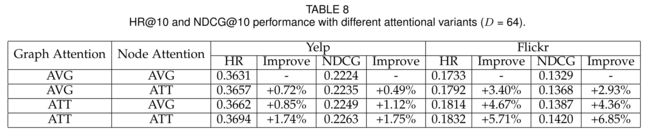
4.3.2 The Effects of Multi-level Attention.
- A key characteristic of our proposed model is the multi-level attention modeling by fusing the social network and interest network for
recommendation. In this subsection, we discuss the effects of different attention mechanisms. We show the results of different attention modeling combinations in in Table 8, (我们提出的模型的一个关键特征是通过融合社交网络和兴趣网络进行推荐,实现了多层次的注意建模。在本小节中,我们将讨论不同注意机制的影响。我们在表8中展示了不同注意建模组合的结果,) - with “AVG” means we directly set the equal attention weights without any attention learning process. As can be observed from this table, either the node level attention or the graph level attention modeling could improve the recommendation results, with the graph level attention shows better results. (AVG的意思是我们直接设置相同的注意力权重,而不需要任何注意力学习过程。从该表可以看出,节点级注意或图级注意建模都可以改善推荐结果,图级注意显示出更好的结果。)
- When combing both the node level attention and the graph level attention, the performance can be further improved. E.g., for the Flickr dataset, the graph level attention improves more than 4% compared to the results of the average attention, and combining the node level attention further improves about 2%. (将节点级注意和图级注意相结合,可以进一步提高性能。例如,对于Flickr数据集,与平均注意的结果相比,图形级注意提高了4%以上,而结合节点级注意进一步提高了约2%。)
- However, the improvement of attention modeling varies in different datasets, with the results of the Yelp dataset is not as significant as the Flickr dataset. (然而,注意建模的改进在不同的数据集中有所不同,Yelp数据集的结果不如Flickr数据集那么显著。)
- This observation implies that the usefulness of considering the importance strength of different elements in the modeling process varies, and our proposed multi-level attention modeling could adapt to different datasets’ requirements. (这一观察结果表明,在建模过程中考虑不同元素的重要性强度的有用性是不同的,我们提出的多级注意建模可以适应不同数据集的需求。)
4.3.3 Attention Value Analysis.
- For each user a a a at layer k k k, the graph level attention weights of γ a 1 k \gamma^k_{a1} γa1k and γ a 2 k \gamma^k_{a2} γa2k denote the social influence diffusion weight and the interest diffusion weight.
- A larger value of γ a 1 k \gamma^k_{a1} γa1k indicates the social influence diffusion process is more important to capture the user embedding learning with less influence from the interest network. ( γ a 1 k γ^k_{a1} γa1k的较大值表明社会影响扩散过程对于捕获用户嵌入学习更为重要,而兴趣网络的影响较小。)
- In Table 9, we show the learned mean and variance of all users’ attention weights at the graph level at each layer k k k. Since both datasets receive the best performance at K K K= 2, we show the attention weights at the first diffusion layer ( k = 1 k = 1 k=1) and the second diffusion layer k = 2 k = 2 k=2. (在表9中,我们展示了在每一层 k k k的图形级别上所有用户注意力权重的学习均值和方差。由于这两个数据集在 K = 2 K=2 K=2时的性能最好,我们显示了第一个扩散层( k = 1 k=1 k=1)和第二个扩散层 k k k=2的注意权重。)
- There are several interesting findings.
- First, we observe for both datasets, at the first diffusion layer with k = 1, the average value of the social influence strength γ a 1 1 \gamma^1_{a1} γa11 are very high, indicating the first-order social neighbors play a very important role in representing each user’s first layer representation. This is quite reasonable as users’ rating behavior are very sparse, and leveraging the first order social neighbors could largely improve the recommendation performance. (首先,我们观察两个数据集,在 k k k=1的第一扩散层,社会影响强度的平均值 γ a 1 1 \gamma^1_{a1} γa11非常高,表明一阶社交邻居在表示每个用户的第一层表示中起着非常重要的作用。这是非常合理的,因为用户的评级行为非常稀疏,利用一阶社交邻居可以大大提高推荐性能。)
- When k= 2, the average social influence strength γ a 1 2 \gamma^2_{a1} γa12 varies among the two datasets, with the Yelp dataset shows a larger average social influence weight, while the Flickr dataset shows a larger interest influence weight with quite small value of average social influence weight. (当k=2时,平均社会影响强度 γ a 1 2 γ^2_{a1} γa12这两个数据集各不相同,Yelp数据集显示出更大的平均社会影响权重,而Flickr数据集显示出更大的兴趣影响权重,平均社会影响权重的值非常小。)
- We guess a possible reason is that, as shown in Table 1, Flickr dataset shows denser social links compared to the Yelp dataset, with a considerable amount of directed social links at the first diffusion layer, the average weight of the second layer social neighbors decreases. (我们猜测一个可能的原因是,如表1所示,与Yelp数据集相比,Flickr数据集显示了更密集的社交链接,在第一扩散层有大量定向社交链接,第二层社交邻居的平均权重降低。)

4.3.4 Runtime.
- In Table 10, we show the runtime of each model on four datasets. Among the four datastes, Epinions and Dianping do not have any attribute information. (在表10中,我们展示了四个数据集上每个模型的运行时间。在这四个数据中,Epinions和Dianping没有任何属性信息。)
- For fair comparison, we perform experiments on a same server. The server has an Intel i9 CPU, 2 Titan RTX 24G, and 64G memory . The classical BPR model costs the least time, followed by the shallow latent factor based social recommendation models of SocailMF and TrustSVD. (为了公平比较,我们在同一台服务器上进行了实验。该服务器有一个Intel i9 CPU、2个Titan RTX 24G和64G内存。经典的BPR模型花费的时间最少,其次是基于浅层潜在因素的社会推荐模型SocailMF和TrustSVD。)
- CNSR has longer runtime as it needs to update both the user embedding learned from user-item behavior, as well as the social embedding learned from user-user behavior. The graph based models cost more time than classical models. (CNSR的运行时间更长,因为它需要更新从用户项行为中学习到的用户嵌入,以及从用户行为中学习到的社交嵌入。基于图形的模型比经典模型花费更多的时间。)
- Specifically, NGCF and DiffNet have similar time complexity as they capture either the interest diffusion or influence diffusion. By injecting both the interest diffusion and influence diffusion process, DiffNet++ costs more time than these two neural graph models. (具体而言,NGCF和DiffNet具有相似的时间复杂度,因为它们捕获的是兴趣扩散或影响扩散。通过注入兴趣扩散和影响扩散过程,DiffNet++比这两种神经图模型花费更多的时间。)
- GraphRec costs the most time on the two datasets without attributes. The reason is that, though GraphRec only considers one-hop graph structure, it adopts a deep neural architecture for modeling the complex interactions between users and items. As we need to use the deep neural architecture for each user-item rating record, GraphRec costs more time than the inner-product based prediction function in DiffNet++. (GraphRec在这两个没有属性的数据集上花费的时间最多。原因是,尽管GraphRec只考虑单跳图结构,但它采用了一种深层的神经结构来建模用户和项目之间的复杂交互。由于我们需要为每个用户项目评级记录使用深层神经结构,GraphRec比DiffNet++中基于内积的预测函数花费更多时间。)
- On Yelp and Flickr, these two datasets have attribute information as input, and the DiffNet++ model needs the fusion layer to fuse attribute and free embeddings, while GraphRec does not have any attribute fusion. (在Yelp和Flickr上,这两个数据集都有属性信息作为输入,DiffNet++模型需要融合层来融合属性和自由嵌入,而GraphRec没有任何属性融合。)
- Therefore, DiffNet++ costs more time than GraphRec on the two datasets with attributes. The average training time of DiffNet++ on the largest Dianping dataset is about 25 seconds for one epoch, and it usually takes less than 100 epoches to reach convergence. Therefore, the total runtime of DiffNet++ is less than 1 hour on the largest dataset, which is also very time efficient. (因此,在具有属性的两个数据集上,DiffNet++比GraphRec花费更多的时间。DiffNet++在最大的Dianping数据集上的平均训练时间约为25秒(一个epoch),通常需要不到100个epoch才能收敛。因此,在最大的数据集上,DiffNet++的总运行时间不到1小时,这也非常节省时间。)

5 CONCLUSIONS AND FUTURE WORK
- In this paper, we presented a neural social and interest diffusion based model, i.e., DiffNet++, for social recommendation. (我们提出了一个基于神经社会和兴趣扩散的社会推荐模型,即DiffNet++。)
- We argued that, as users play a central role in social network and interest network, jointly modeling the higher-order structure of these two networks would mutually enhance each other. (我们认为,由于用户在社交网络和兴趣网络中扮演着核心角色,联合建模这两个网络的高阶结构将相互增强。)
- By formulating the social recommendation as a heterogeneous graph, we recursively learned the user embedding from convolutions on user social neighbors and interest neighbors, such that both the higher-order social structure and higher-order interest network are directly injected in the user modeling process. (通过将社会推荐描述为一个异构图,我们递归地从用户社会邻居和兴趣邻居的卷积中学习用户嵌入,从而在用户建模过程中直接注入高阶社会结构和高阶兴趣网络。)
- Furthermore, we designed a multi-level attention network to attentively aggregate the graph and node level representations for better user modeling. (此外,我们还设计了一个多层次的注意网络,将图形和节点级别的表示集中起来,以便更好地进行用户建模。)
- Experimental results on two real-world datasets clearly showed the effectiveness of our proposed model. In the future, we would like to explore the graph reasoning models to explain the paths for users’ behaviors.