【GCN-RS】Deep GCN with Hybrid Normalization for Accurate and Diverse Recommendation (DLP-KDD‘21)

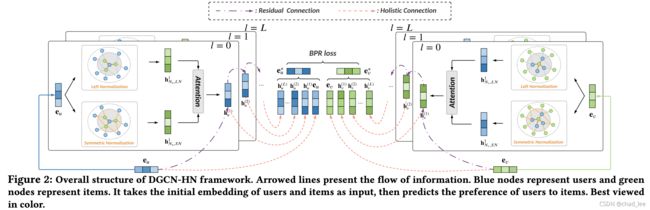
Deep Graph Convolutional Networks with Hybrid Normalization for Accurate and Diverse Recommendation (DLP-KDD’21)

一句话总结这篇文章就是在LR-GCCF和LightGCN的基础上，同时结合了 left normalization (给不同的邻居分配相等的归一化，PinSAGE)和 symmetric normalization （degree大的邻居分配小权重，LightCGN）。

Abstract

摘要完全概括了文章的内容：

现有的GCN RS模型在浅层就达到了最佳性能，这就没有用到高阶信号；现有的GCN模型对邻居信号聚合时，使用相同的归一化规则，要么PinSAGE那样同等重要，要么是LightGCN那样根据degree分配重要性。

但是同一套归一化规则肯定不能适配所有节点，所以提出了一个新的模型Deep Graph Convolutional Network with Hybrid Normalization (DGCN-HN)。

首先设计了一个residual connection 和 holistic connection**（LR-GCCF和LightGCN的混合版）**，以解决over-smoothing，可以训练深层GCN（8层）。

然后设计了hybrid normalization layer。通过一个简化的attention**（正常的attention没用）**实现hybrid 两种正则化。

实验结果还证明了这种做法有利于degree低的user。

Intro

又强调了一边现在的GCN RS都不深、使用了固定的归一化规则，使用相同的归一化规则会导致局部最优。

文章用一个例子解释了上述缺点：

• 浅层GCN不能利用高阶信号，给喜欢电子产品的U2推荐无人机就需要高阶信号。
• 给所有节点使用 left normalization ，流行度很高的IPhone就会严重影响U1的兴趣，U1买IPhone只是刚需，兴趣并不在电子产品，因为U1经常购买纸质文具。
• 给所有节点使用 symmetric normalization，流行度很高的IPhone就无法提供”电子产品“这一兴趣，U2和U3的兴趣就难以被刻画出来。

Model

所谓Residual就是在LightGCN的基础上加一个Residual：
$$\begin{array}{rl}{\mathbf{h}}_u^{(l+1)}& =\sum _{v\in N_u}{\tilde{\mathrm{A}}}_{uv}{\mathbf{h}}_v^{(l)}+{\mathbf{h}}_u^{(l)},{\mathbf{h}}_u^{(0)}={\mathbf{e}}_u\\ {\mathbf{h}}_v^{(l+1)}& =\sum _{u\in N_v}{\tilde{\mathrm{A}}}_{vu}{\mathbf{h}}_u^{(l)}+{\mathbf{h}}_v^{(l)},{\mathbf{h}}_v^{(0)}={\mathbf{e}}_v\end{array}$$

${\tilde{\mathrm{A}}}_{uv}$ 是Hybrid Normalization，混合了left normalization 和 symmetric normalization。一个简单的想法肯定两种正则化平均嘛，那进一步的想法就是做一个加权平均，上Attention：
$$\begin{array}{rl}{\mathbf{h}}_{N_u,LN}^{(l+1)}& =\sum _{v\in N_u}\frac{1}{\left|N_u\right|}{\mathbf{h}}_v^{(l)}\\ {\mathbf{h}}_{N_u,SN}^{(l+1)}& =\sum _{v\in N_u}\frac{1}{\sqrt{\left|N_u\right|}\sqrt{\left|N_v\right|}}{\mathbf{h}}_v^{(l)}\\ {\mathbf{h}}_u^{(l+1)}& ={\mathbf{h}}_u^{(l)}+{\alpha }_{u,LN}^{(l+1)}{\mathbf{h}}_{N_u,LN}^{(l+1)}+{\alpha }_{u,SN}^{(l+1)}{\mathbf{h}}_{N_u,SN}^{(l+1)}\end{array}$$
怎么算 Attention score？作者设计了一个Attention Layer：
$$z_{u,\ast }^{(l+1)}={\mathrm{W}}_1^{(l)}\sigma \left({\mathrm{W}}_2^{(l)}\left({\mathrm{h}}_{N_u,\ast }^{(l+1)}+{\mathrm{h}}_{N_u,\ast }^{(l+1)}\odot {\mathrm{h}}_u^{(l)}\right)\right)$$
结果实验上训不起来无法收敛，换了一个简单的：
$$z_{u,\ast }^{(l+1)}=\mathrm{ave}\left({\mathbf{h}}_{N_u,\ast }^{(l+1)}+{\mathbf{h}}_{N_u,\ast }^{(l+1)}\odot {\mathbf{h}}_u^{(l)}\right)$$

$${\alpha }_{u,\ast }^{(l)}=\frac{\exp \left(z_{u,\ast }^{(l)}\right)}{{\sum }_{k\in \{LN,SN\}}\exp \left(z_{u,k}^{(l)}\right)}$$

Loss就是BPR loss，负采样比例1

实验结果

提出的模型可以训到八层：

从Recall上看left normalization 和 symmetric normalization结合起来性能最好：

文章从实验结果分析，对degree低的user提升更大：

我觉得是正常现象强行分析，因为degree低的user recall本来就低，基数小，所以显得提升大。