《玩转数据结构 从入门到进阶》红黑树
《数据结构与算法》
本文来源于liuyubobobo的“玩转数据结构 从入门到进阶”视频教程
本教程是基于二分搜索树实现红黑树,请先看 《玩转数据结构 从入门到进阶》二分搜索树 Binary Search Tree
红黑树也有左旋转、右旋转这种操作,如果不了解,请先阅读 《玩转数据结构 从入门到进阶》平衡二叉树AVL
由于红黑树的定义太过于复杂,所以先学习2-3树,然后通过红黑树与2-3树对比,才能更好的理解红黑树。
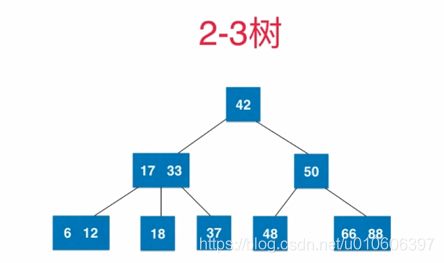
2-3树
2-3树满足二分搜索树的基本性质,但其节点可以存放一个元素或者两个元素,2-3是一颗绝对平衡的树。
下图是一颗2-3树
下面用图展示向2-3树加入节点的过程
可以总结出一个规律,给2-3树添加一个节点,此节点必然是首先和某个节点融合。如果直接把新节点加入成某个节点的子节点,那必然会破坏树的绝对平衡。
下图展示把6加入到树中的过程
下图展示把5加入到树中的过程
了解了2-3树之后,就可以来学习红黑树了。先用2-3树和红黑树做一个类比
 通过2-3树和红黑树的类比,就大致能理解红黑树是一个什么东西了,下面给出红黑树的定义。
通过2-3树和红黑树的类比,就大致能理解红黑树是一个什么东西了,下面给出红黑树的定义。
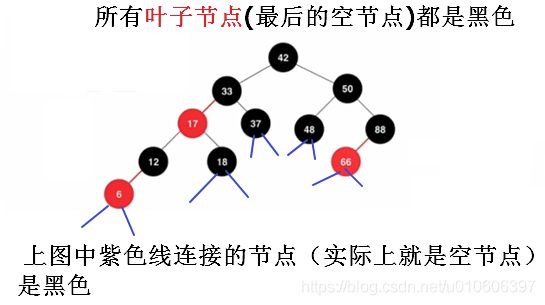
红黑树是每个节点都带有颜色属性的二叉查找树,颜色为红色或黑色。在二叉查找树强制一般要求以外,对于任何有效的红黑树我们增加了如下的额外要求
1、节点是红色或者黑色
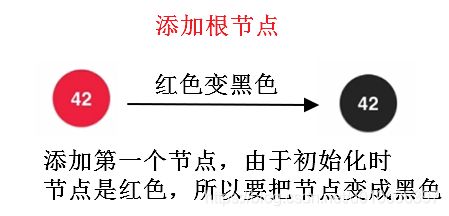
2、根节点是黑色
3、所有叶子节点(最后的空节点)都是黑色
4、如果一个节点是红色,那么它的孩子节点都是黑色
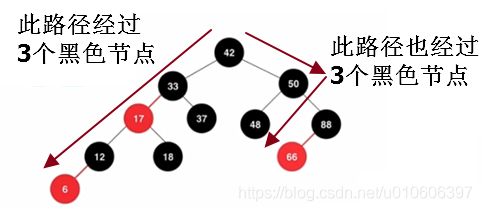
5、从任意一个节点到子节点,经过的黑色节点个数是相同的
3、5不容易理解,下面用图解释
3、所有叶子节点(最后的空节点)都是黑色
5、从任意一个节点到子节点,经过的黑色节点个数是相同的
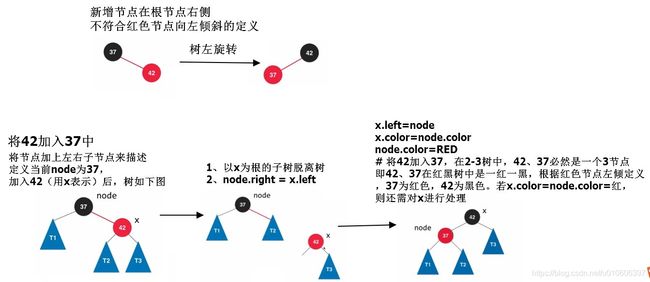
本教程实现的红黑树是以红色节点左倾斜为基础的红黑树。
使用《玩转数据结构 从入门到进阶》二分搜索树 Binary Search Tree 中的代码为基础,编写红黑树代码
public class RBTree, V> {
// 定义红黑树颜色
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node{
public K key;
public V value;
public Node left, right;
public boolean color;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
/**
* 初始化一个红黑树节点,首先将节点设置为红色,
* 在将节点添加到树中时,可能会将节点颜色改成黑色
*/
color = RED;
}
}
private Node root;
private int size;
public RBTree(){
root = null;
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
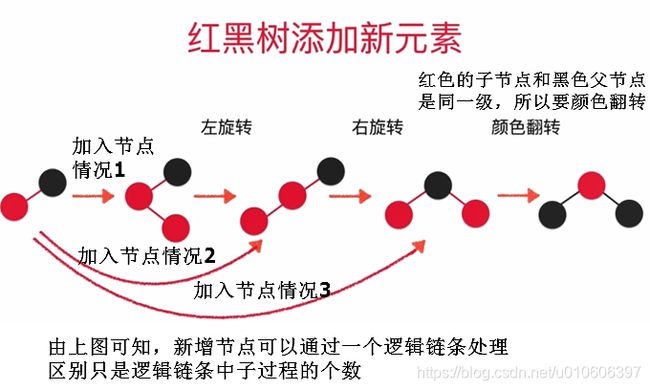
} 添加节点的过程
左旋转代码
// node x
// / \ 左旋转 / \
// T1 x ---------> node T3
// / \ / \
// T2 T3 T1 T2
private Node leftRotate(Node node){
Node x = node.right;
// 左旋转
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
/**
* 若出现x.color = node.color=RED; node.color = RED; 的情况
* 由于我们已经将x节点返回给调用者,调用者就可以处理x的颜色了
*/
return x;
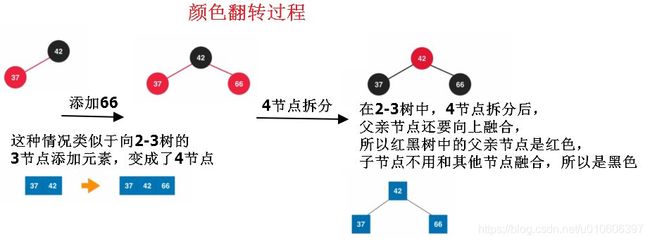
}颜色翻转代码
// 颜色翻转
private void flipColors(Node node){
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
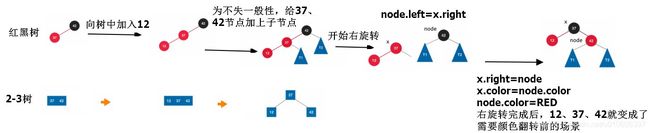
}右旋转代码
// node x
// / \ 右旋转 / \
// x T2 -------> y node
// / \ / \
// y T1 T1 T2
private Node rightRotate(Node node){
Node x = node.left;
// 右旋转
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
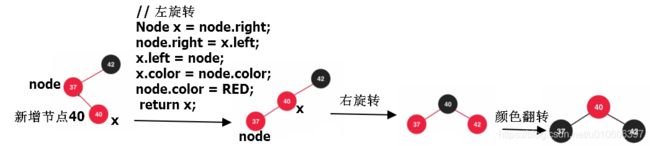
}需要左右旋转+颜色翻转的情况
红黑树的添加节点代码(删除代码太复杂,不写了)
public class RBTree, V> {
// 定义红黑树颜色
private static final boolean RED = true;
private static final boolean BLACK = false;
private class Node{
public K key;
public V value;
public Node left, right;
public boolean color;
public Node(K key, V value){
this.key = key;
this.value = value;
left = null;
right = null;
/**
* 初始化一个红黑树节点,首先将节点设置为红色,
* 在将节点添加到树中时,可能会将节点颜色改成黑色
*/
color = RED;
}
}
private Node root;
private int size;
public RBTree(){
root = null;
size = 0;
}
public int getSize(){
return size;
}
public boolean isEmpty(){
return size == 0;
}
// 判断节点node的颜色
private boolean isRed(Node node){
if(node == null)
return BLACK;
return node.color;
}
// 返回以node为根节点的二分搜索树中,key所在的节点
private Node getNode(Node node, K key){
if(node == null)
return null;
if(key.equals(node.key))
return node;
else if(key.compareTo(node.key) < 0)
return getNode(node.left, key);
else // if(key.compareTo(node.key) > 0)
return getNode(node.right, key);
}
public boolean contains(K key){
return getNode(root, key) != null;
}
public V get(K key){
Node node = getNode(root, key);
return node == null ? null : node.value;
}
public void set(K key, V newValue){
Node node = getNode(root, key);
if(node == null)
throw new IllegalArgumentException(key + " doesn't exist!");
node.value = newValue;
}
// node x
// / \ 左旋转 / \
// T1 x ---------> node T3
// / \ / \
// T2 T3 T1 T2
private Node leftRotate(Node node){
Node x = node.right;
// 左旋转
node.right = x.left;
x.left = node;
x.color = node.color;
node.color = RED;
/**
* 若出现x.color = node.color=RED; node.color = RED; 的情况
* 由于我们已经将x节点返回给调用者,调用者就可以处理x的颜色了
*/
return x;
}
// node x
// / \ 右旋转 / \
// x T2 -------> y node
// / \ / \
// y T1 T1 T2
private Node rightRotate(Node node){
Node x = node.left;
// 右旋转
node.left = x.right;
x.right = node;
x.color = node.color;
node.color = RED;
return x;
}
// 颜色翻转
private void flipColors(Node node){
node.color = RED;
node.left.color = BLACK;
node.right.color = BLACK;
}
// 以二分搜索树添加方法为基础改造为红黑树的添加方法
// 向红黑树中添加新的元素(key, value)
public void add(K key, V value){
root = add(root, key, value);
root.color = BLACK; // 保持红黑树根节点一直为黑色
}
private Node add(Node node, K key, V value){
if(node == null){
size ++;
return new Node(key, value);
}
if(key.compareTo(node.key) < 0)
node.left = add(node.left, key, value);
else if(key.compareTo(node.key) > 0)
node.right = add(node.right, key, value);
else
node.value = value;
// 根据条件节点后的逻辑链条,编写处理情况
// 是否左旋转
if (isRed(node.right) && !isRed(node.left))
node = leftRotate(node);
// 是否右旋
if (isRed(node.left) && isRed(node.left.left))
node = rightRotate(node);
// 是否颜色和翻转
if (isRed(node.left) && isRed(node.right))
flipColors(node);
// 这3个判断条件不是if-else的关系,判断顺序也不能变
// 由于是递归代码,假如返回的node是红色,则node返回给调用者后,还会执行上面的3个判断
return node;
}
public static void main(String[] args){
/**
* 读取傲慢与偏见这本书,通过 “单词”:“单词在书中出现的次数” 这种key-value的形式把书中的单词-词频加到AVLTree中
* FileUtil、傲慢与偏见.txt 可以到我的github下载
* https://github.com/CodingSoldier/java-learn/tree/master/note/src/main/java/com/datastructure
*/
ArrayList words = new ArrayList<>();
if(FileUtil.readFile("./note/src/main/java/com/datastructure/傲慢与偏见.txt", words)) {
System.out.println("总单词数: " + words.size());
RBTree map = new RBTree<>();
for (String word : words) {
if (map.contains(word))
map.set(word, map.get(word) + 1);
else
map.add(word, 1);
}
System.out.println("单词去重后的总数: " + map.getSize());
}
}
} 红黑树的最大高度是2logN(N是树的size),查询性能比AVL差。但是新增、删除性能要比AVL好。总体来说红黑树的综合性能比AVL好。