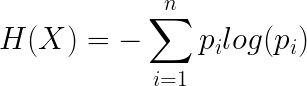机器学习笔记——决策树(Decision Tree)（1）

决策树​​​​​​​
1.引入

  1.1定义

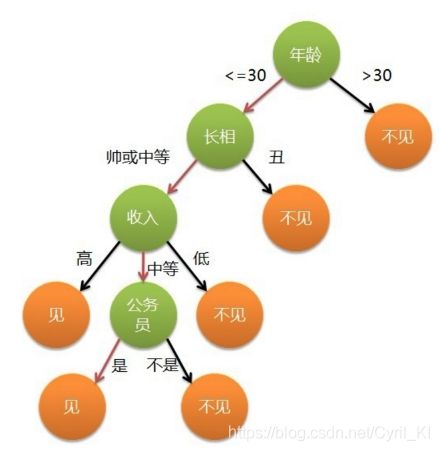
决策树，顾名思义，就是帮我们做出决策的树。现实生活中我们往往会遇到各种各样的抉择，把我们的决策过程整理一下，就可以发现，该过程实际上就是一个树的模型。比如相亲的时候：

我们可以认为年龄，长相，收入是一个人的三个特征，每次我们做出抉择都是基于这三个特征来把一个节点分成好几个新的节点。
  一颗完整的决策树包含以下三个部分：

        1.1.1根节点：

就是树最顶端的节点，比如上面图中的“年龄”。

        1.1.2叶子节点：

树最底部的那些节点，也就是决策结果，见还是不见。

        1.1.3内部节点

除了叶子结点，都是内部节点。
        原文链接：https://blog.csdn.net/Cyril_KI/article/details/107162316

2.本文数据集的选择

        Car Evaluation Data Set        

        UCI Machine Learning Repository: Car Evaluation Data Set

         这是一个关于汽车测评的数据集，类别变量为汽车的测评，（unacc，ACC，good，vgood）分别代表（不可接受，可接受，好，非常好），而6个属性变量分别为「买入价」，「维护费」，「车门数」，「可容纳人数」，「后备箱大小」，「安全性」。值得一提的是6个属性变量全部是有序类别变量，比如「可容纳人数」值可为「2，4，more」，「安全性」值可为「low, med, high」。

数据集特征:	多变量	记录数:	1728	领域:	N/A
属性特征:	类别型	属性数目:	6	捐赠日期	1997-06-01
相关应用:	分类	缺失值?	无	网站点击数:	272901

本文代码大量参考于《机器学习实战》

 3.决策树的生成算法

        3.1思想：

        构建决策树，首先我们要选择一个根节点，那么选谁当做根节点呢？比如本文的例子，有「买入价」，「维护费」，「车门数」，「可容纳人数」，「后备箱大小」，「安全性」六个属性，所以我们要在六个当中选择一个。以六个属性分别为根节点可以生成六棵树（从第一层到第二层），而究竟选择谁来当根节点的准则，有以下三种。

        3.2信息熵

        3.2.1概念

        我们用信息熵来描述一个事件混乱程度的大小（一个事件我们一定知道结果，那么这个事件的混乱程度就是0；一个时间充满随机性，我们猜不到或者很难猜到结果，那么他的混乱度就很大），如：如果一枚硬币的两面完全相同，那个这个系列抛硬币事件的熵等于零，因为结果能被准确预测。现实世界里，我们收集到的数据的熵介于上面两种情况之间。

        依据Boltzmann’s H-theorem，香农把随机变量X的熵值 Η（希腊字母Eta）定义如下，其值域为{x1, …, xn}： 

 其中，P为X的概率质量函数（probability mass function），E为期望函数，而I(X)是X的信息量（又称为自信息）。I(X)本身是个随机变数。

 香农的信息熵本质上是对我们司空见惯的“不确定现象”的数学化度量。 

        3.2.2python代码实现

from math import log
#from numpy import *#
import numpy as np
import operator
import matplotlib.pyplot as plt
'''
计算数据集香农熵
dataSet - 待划分的数据集
'''
def calcShannonEnt(dataSet):
    # 返回数据集的行数
    numEntries = len(dataSet)
    # 保存每个标签（Label）出现次数
    labelCounts = {}
    for featVec in dataSet:
        # 提取标签信息
        currentLabel = featVec[-1]
        # 选择该标签（Label）的概率
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    shannonEnt = 0.0
    # 选择该标签的概率
    for key in labelCounts:
        prob = float(labelCounts[key])/numEntries
        shannonEnt -= prob * log(prob,2)
# 利用公式计算
return shannonEnt
# 返回香农熵(以2为底称为香农熵)

        3.2.3调试时出现的问题           

        上面这段代码在运行时会出现 TypeError: return arrays must be of ArrayType的错误，因为log的第二个参数不是base而是out array。如果你只是想执行普通的log操作，可以选择使用numpy.math.log(1.1, 2)或者使用python自带的math模块的log函数，注意库的调用，本文使用math模块的log函数。

        3.2.4为什么要使用log

香农发现 lnx, x∈[0,1] 符合信息的量化应该遵循的原则：

• 信息是非负的
• 如果一件事物发生的概率是1（没有选择的自由度），信息量为0。（越确定的事件越不混乱）
• 如果两件事物的发生是独立的（联合概率），它们一起发生时我们获得的信息是两者单独发生的信息之和。
• 信息的度量应该是概率的函数，函数最好是单调连续的。

思考方式在下面参考资料讲得非常清楚

一文看懂信息熵的本质——谈谈自己对信息熵的理解_StudentWang_的博客-CSDN博客

3.3信息增益与ID3

        3.3.1概念

        决策树中信息增益定义如下：
  给定一个样本集D，划分前样本集合D的熵是一定的 ，用H0表示； 使用某个特征A划分数据集D，计算划分后的数据子集的熵，用H1表示，则：
  信息增益=H0-H1，也可以表示为：
​

         利用信息增益作为选择指标来生成决策树的算法称为ID3算法。

      3.3.2python代码实现

        splitDataSet(dataSet,axis,value):#按照给定特征划分数据集

        三种生成算法都需要调用这个方法，当计算出需要哪个特征作为根节点的时候，要将数据集分类，如本文将safety作为根节点，数据集就需要将根节点以[safety]的特征值「low, med, high」分类为三个数据集，然后继续递归调用创造决策树。

'''
定义按照某个特征进行划分的函数splitDataSet
输入三个变量（待划分的数据集，特征，分类值）
axis表示划分数据集的特征
value分类值
'''
def splitDataSet(dataSet,axis,value):#按照给定特征划分数据集
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis+1:])            
            retDataSet.append(reducedFeatVec)
    # 返回划分后的数据集
    return retDataSet

'''
#选择信息增益最大的（最优）特征作为数据集划分方式
dataSet - 待划分的数据集
'''
def chooseBeatFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0])-1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0
    bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet,i,value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob*calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
                # 打印每个特征的信息增益
        print("第%d个特征的增益为%.3f" % (i, infoGain))
        if(infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    print("选择%d"%bestFeature)
    # 返回信息增益最大的特征的索引值
    return bestFeature

3.4信息增益率与C4.5

3.4.1概念

 C4.5算法是用于生成决策树的一种经典算法，是ID3算法的一种延伸和优化。C4.5算法对ID3算法主要做了一下几点改进：
  （1）通过信息增益率选择分裂属性，克服了ID3算法中通过信息增益倾向于选择拥有多个属性值的属性作为分裂属性的不足；

        信息增益可能会导致一些属性多的属性特征获得更高的信息增益，因此导致最终决策树分支过多，分支过多容易导致过拟合，为了解决信息增益的局限，引入了信息增益率的概念。

        大的数除以一个大的数，刚好可以中和一下。
  *（2）能够处理离散型和连续型的属性类型，即将连续型的属性进行离散化处理；
  *（3）构造决策树之后进行剪枝操作；
  *（4）能够处理具有缺失属性值的训练数据。

  3.4.2python代码实现

和信息增益差的不多

def chooseBestFeatureToSplit(dataSet):
    # 特征数量
    numFeatures = len(dataSet[0]) - 1  # 最后一列为label
    # 计算数据集的香农熵
    baseEntropy = calcShannonEnt(dataSet)
    # 信息增益
    bestInfoGain = 0.0
    # 最优特征的索引值
    bestFeature = -1
    # 遍历所有特征
    for i in range(numFeatures):
        # 获取dataSet的第i个所有特征存在featList这个列表中（列表生成式）
        featList = [example[i] for example in dataSet]
        # 创建set集合{}，元素不可重复，重复的元素均被删掉
        # 从列表中创建集合是python语言得到列表中唯一元素值得最快方法
        uniqueVals = set(featList)
        # 经验条件熵
        newEntropy = 0.0
        # 计算信息增益
        for value in uniqueVals:
            # subDataSet划分后的子集
            subDataSet = splitDataSet(dataSet, i, value)
            # 计算子集的概率
            prob = len(subDataSet) / float(len(dataSet))
            # 根据公式计算经验条件熵
            newEntropy += prob * calcShannonEnt(subDataSet)
        # 信息增益
        infoGain = baseEntropy - newEntropy
        # 打印每个特征的信息增益
        print("第%d个特征的增益为%.3f" % (i, infoGain))
        # 计算信息增益
        if (infoGain > bestInfoGain):
            # 更新信息增益，找到最大的信息增益
            bestInfoGain = infoGain
            # 记录信息增益最大的特征的索引值
            bestFeature = i
    # 返回信息增益最大的特征的索引值
    return bestFeature

def chooseBestFeatureToSplitRatio(dataSet):
    # 特征数量
    numFeatures = len(dataSet[0]) - 1  # 最后一列为label
    # 计算数据集的香农熵
    baseEntropy = calcShannonEnt(dataSet)
    # 信息增益
    bestInfoGain = 0.0
    # 最优特征的索引值
    bestFeature = -1
    # 遍历所有特征
    for i in range(numFeatures):
        # 获取dataSet的第i个所有特征存在featList这个列表中（列表生成式）
        featList = [example[i] for example in dataSet]
        # 创建set集合{}，元素不可重复，重复的元素均被删掉
        # 从列表中创建集合是python语言得到列表中唯一元素值得最快方法
        uniqueVals = set(featList)
        # 经验条件熵
        newEntropy = 0.0

        IV = 0.0
        # 计算信息增益
        for value in uniqueVals:
            # subDataSet划分后的子集
            subDataSet = splitDataSet(dataSet, i, value)
            # 计算子集的概率
            prob = len(subDataSet) / float(len(dataSet))
            # 根据公式计算经验条件熵
            newEntropy += prob * calcShannonEnt(subDataSet)
            IV -= prob * log(prob, 2)
        # 信息增益
        infoGain = baseEntropy - newEntropy
        # 信息增益率
        if IV == 0:
            IV = 1
        infoGainRatio = infoGain / IV
        # 打印每个特征的信息增益
        print("第%d个特征的增益率为%.3f" % (i, infoGainRatio))
        # 计算信息增益率
        if (infoGainRatio > bestInfoGain):
            # 更新信息增益率，找到最大的信息增益率
            bestInfoGain = infoGainRatio
            # 记录信息增益率最大的特征的索引值
            bestFeature = i
    # 返回信息增益率最大的特征的索引值
    return bestFeature

3.5基尼指数

3.5.1概念

 关于基尼系数的理解，网上有一种说法比较通俗易懂。现解释如下：
  我们知道信息熵的定义式为：

        

 那么基尼系数实际上就是用1 − pi 来代替了− l o g ( p i ) ：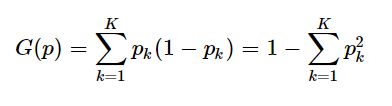

画出二者图像:

因为概率是属于0到1之间，所以我们只看01区间上的图像：基尼系数对于信息熵而言，就是在01区间内近似的用切线来代替了对数函数。因此，既然信息熵可以表述不确定度，那么基尼系数自然也可以，只不过存在一些误差。 

计算分配到错误答案的概论,这一概率越高，说明对数据的拆分越不合理。因此，我们选出基尼指数最低的属性

  3.5.2python代码实现

def gini(dataSet):
    # 返回数据集的行数
    numEntires = len(dataSet)
    # 保存每个标签（Label）出现次数的“字典”
    labelCounts = {}
    # 对每组特征向量进行统计
    for featVec in dataSet:
        # 提取标签（Label）信息
        currentLabel = featVec[-1]
        # 如果标签（Label）没有放入统计次数的字典，添加进去
        if currentLabel not in labelCounts.keys():
            # 创建一个新的键值对，键为currentLabel值为0
            labelCounts[currentLabel] = 0
        # Label计数
        labelCounts[currentLabel] += 1
    # 经验熵（香农熵）
    shannonEnt = 0.0
    # 计算香农熵
    for key in labelCounts:
        # 选择该标签（Label）的概率
        prob = float(labelCounts[key]) / numEntires
        # 利用公式计算
        shannonEnt = pow(prob, 2)
    # 返回经验熵（香农熵）
    print("SHANNO=", 1 - shannonEnt)
    return 1 - shannonEnt
    
    
def chooseBestFeatureToSplitGini(dataSet):
    # 特征数量
    numFeatures = len(dataSet[0]) - 1  # 最后一列为label
    print(numFeatures)
    # 计算数据集的香农熵
    baseEntropy = calcShannonEnt(dataSet)
    # 信息增益
    bestInfoGain = 100
    # 最优特征的索引值
    bestFeature = -1
    # 遍历所有特征
    for i in range(numFeatures):
        # 获取dataSet的第i个所有特征存在featList这个列表中（列表生成式）
        featList = [example[i] for example in dataSet]
        print(featList)
        # 创建set集合{}，元素不可重复，重复的元素均被删掉
        # 从列表中创建集合是python语言得到列表中唯一元素值得最快方法
        uniqueVals = set(featList)
        # 经验条件熵
        print(uniqueVals)
        gini_index = 0.0
        # 计算信息增益
        for value in uniqueVals:
            # subDataSet划分后的子集
            subDataSet = splitDataSet(dataSet, i, value)
            # 计算子集的概率
            prob = len(subDataSet) / float(len(dataSet))
            #print("第%d个特征的prob为%.3f" % (value, prob))
            # 根据公式计算基尼指数
            gini_index += prob * gini(subDataSet)

        # 打印每个特征的信息增益
        print("第%d个特征的基尼指数为%.3f" % (i, gini_index))
        # 计算基尼指数
        if (gini_index < bestInfoGain):
            # 更新基尼指数，找到最大的基尼指数
            bestInfoGain = gini_index
            # 记录基尼指数最小的特征的索引值
            bestFeature = i
    # 返回基尼指数最小的特征的索引值
    return bestFeature

3.5构造决策树及画图

def majorityCnt(classList):
    classCount = {}
    for vote in classCount:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
        sortedClassCount = sorted(classCount.items(),key=operator.itemgetter(1),reverse=True)
        return sortedClassCount[0][0]


def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0])==len(classList):
        return classList[0]
    if len(dataSet[0])==1:
        return majorityCnt(classList)
    beatFeat = chooseBeatFeatureToSplit(dataSet)
    #beatFeat = chooseBestFeatureToSplitRatio(dataSet)
    #beatFeat = chooseBestFeatureToSplitGini(dataSet)
    beatFeatLable = labels[beatFeat]
    myTree = {beatFeatLable:{}}
    del(labels[beatFeat])
    featValues = [example[beatFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[beatFeatLable][value] = createTree(splitDataSet\
                                                (dataSet,beatFeat,value),subLabels)
    return myTree


decisionNode = dict(boxstyle='sawtooth',fc='0.8')
leafNode = dict(boxstyle='round4',fc='0.8')
arrow_args = dict(arrowstyle='<-')

def plotNode(nodeText,centerPt,parentPt,nodeType):
# nodeTxt为要显示的文本，centerPt为文本的中心点，parentPt为指向文本的点 
    createPlot.ax1.annotate(nodeText,xytext=centerPt,textcoords="axes fraction",\
                        xy=parentPt,xycoords="axes fraction",\
                       va="center",ha="center",bbox=nodeType,arrowprops=arrow_args)
# 求叶子节点数
def getNumLeafs(myTree):
    numNode = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            numNode += getNumLeafs(secondDict[key])
        else:
            numNode += 1
    return numNode

#获取决策树的深度
def getTreeDepth(myTree):
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
    return thisDepth

#预定义的树，用来测试
def retrieveTree(i):
    listOfTrees = [
        {'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}},
        {'no surfacing': {0: 'no', 1: {'flippers': {0: {'head': {0: 'no', 1: 'yes'}}, 1: 'no'}}}}
    ]
    return listOfTrees[i]

#绘制中间文本（在父子节点间填充文本信息）
def plotMidText(cntrPt,parentPt,txtString):
    #求中间点的横坐标
    xMid = (parentPt[0]- cntrPt[0])/2.0 + cntrPt[0]
    #求中间点的纵坐标
    yMid = (parentPt[1] - cntrPt[1])/2.0 + cntrPt[1]
    #绘制树节点
    createPlot.ax1.text(xMid,yMid,txtString,va='center',ha='center',rotation=30)
#绘制决策树
def plotTree(myTree,parentPt,nodeTxt):
    #获得决策树的叶子节点数与深度
    numLeafs = getNumLeafs(myTree)
    depth = getTreeDepth(myTree)
    #firstStr = myTree.keys()[0]
    firstSides = list(myTree.keys())
    firstStr = firstSides[0]
    cntrPt = (plotTree.xOff + (1.0 + float(numLeafs))/2.0/plotTree.totalw,plotTree.yOff)
    #print('c:',cntrPt)
    plotMidText(cntrPt,parentPt,nodeTxt)
    plotNode(firstStr,cntrPt,parentPt,decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff - 1.0/plotTree.totalD
    #print('d:',plotTree.yOff)
    for key in secondDict.keys():
        #如果secondDict[key]是一颗子决策树，即字典
        if type(secondDict[key]) is dict:
            #递归地绘制决策树
            plotTree(secondDict[key],cntrPt,str(key))
        else:
            plotTree.xOff = plotTree.xOff + 1.0/plotTree.totalw
            #print('e:',plotTree.xOff)
            plotNode(secondDict[key],(plotTree.xOff,plotTree.yOff),cntrPt,leafNode)
            plotMidText((plotTree.xOff,plotTree.yOff),cntrPt,str(key))
    plotTree.yOff = plotTree.yOff + 1.0/plotTree.totalD
    #print('f:',plotTree.yOff)

#创建决策树
def createPlot(inTree):
    fig = plt.figure(1,facecolor='white')
    fig.clf()
    axprops = dict(xticks=[],yticks=[])
    createPlot.ax1 = plt.subplot(111,frameon=False, **axprops)
    plotTree.totalw = float(getNumLeafs(inTree))
    plotTree.totalD = float(getTreeDepth(inTree))
    plotTree.xOff = -0.5/plotTree.totalw
    plotTree.yOff = 1.0
    plotTree(inTree,(0.5,1.0),'')
    plt.show()

这两个方法分别用于文件读取和文本预处理数据集中的训练集和测试集。

def loadData():
    fr = open('car/rand_cardata.txt')
    lines = fr.readlines()
    retData = []
    for line in lines:
        items = line.strip().split(',')
        retData.append([items[i] for i in range(0, len(items))])
    return retData

def loadData1():
    fr = open('car/Testcardata1.txt')
    lines = fr.readlines()
    retData = []
    for line in lines:
        items = line.strip().split(',')
        retData.append([items[i] for i in range(0, len(items))])
    return retData

3.7测试

from numpy import *
from sklearn.datasets import load_iris
from sklearn import datasets
import trees
#import array as ar
carData = trees.loadData()
TestcarData = trees.loadData1()
carLabels = ['buying','maint','doors','persons','lug_boot','safety']
#「买入价」，「维护费」，「车门数」，「可容纳人数」，「后备箱大小」，「安全性」汽车测评的数据集
carTree = trees.createTree(carData,carLabels)
trees.createPlot(carTree)
ans = [example[-1] for example in TestcarData]
result = []

# 测试数据
#testArr = ar.array(testArr)
for i in range(len(TestcarData)):
    resu = trees.classify(carTree,['buying','maint','doors','persons','lug_boot','safety'], TestcarData[i])  
    #print(resu)
    result.append(resu)#在列表末尾添加新的对象'
#print(result)
#print(ans)
#
for i in range(len(TestcarData)):
    result = array(result)#从队列中取出
    ans = array(ans)
    accuracy = mean(result == ans)
print("训练数据",len(carData),"份,测试数据",len(TestcarData),"份,准确率为:",accuracy)

分别对信息增益，信息增益率，基尼指数，三种方法进行测试（在create树中调整）

3.8实验结果

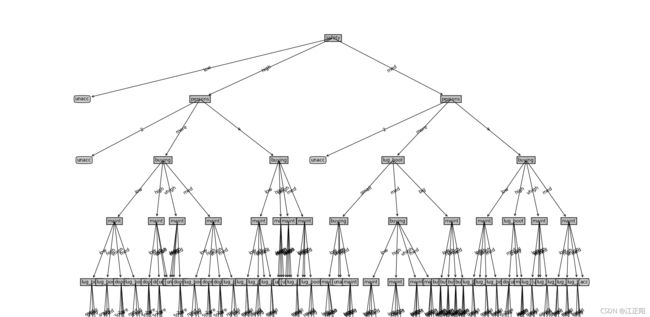
3.8.1信息增益实验结果及可视化

对测试集预测准确率 ：0.91666

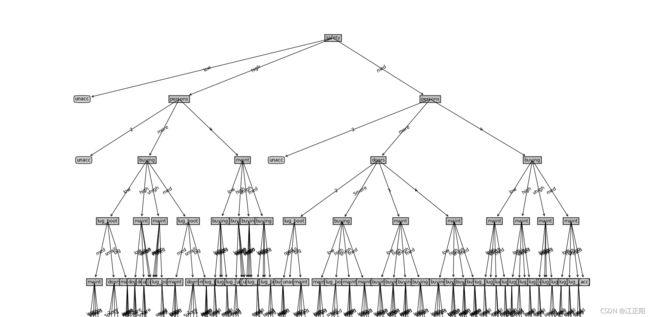
3.8.2信息增益率实验结果及可视化

对测试集预测准确率 ：0.92153

3.8.3基尼指数实验结果及可视化

 对测试集预测准确率 ：0.89474

 3.9总结

1.决策树算法主要包括三个部分：特征选择、树的生成、树的剪枝。常用算法有 ID3、C4.5、CART。

• 特征选择。特征选择的目的是选取能够对训练集分类的特征。特征选择的关键是准则：信息增益、信息增益比、Gini 指数；
• 决策树的生成。通常是利用信息增益最大、信息增益比最大、Gini 指数最小作为特征选择的准则。从根节点开始，递归的生成决策树。相当于是不断选取局部最优特征，或将训练集分割为基本能够正确分类的子集；
• 决策树的剪枝。决策树的剪枝是为了防止树的过拟合，增强其泛化能力。包括预剪枝和后剪枝。

2.实验结果

        对数据的预测都差不多能达到90%的正确率，从可视化树来看，可能由于数据集特征大部分都是三到四个属性，导致三种方法的树差别的地方不是特别多，不过都有一个问题就是过拟合。  

按照数据集来看70%的数据结果为unacceptable，虽然正确率还行，但是这样的树效率较低，缺少预剪枝或者剪枝的过程，留个坑，在决策树（二）中实现。

  class      N          N[%]
   -----------------------------
   unacc     1210     (70.023 %) 
   acc        384     (22.222 %) 
   good        69     ( 3.993 %) 
   v-good      65     ( 3.762 %) 

3.决策树优点缺点

• 决策树学习可能创建一个过于复杂的树，并不能很好的预测数据。也就是过拟合。修剪机制（现在不支持），设置一个叶子节点需要的最小样本数量，或者数的最大深度，可以避免过拟合。
• 决策树可能是不稳定的，因为即使非常小的变异，可能会产生一颗完全不同的树。
•  传统决策树算法基于启发式算法，例如贪婪算法，即每个节点创建最优决策。这些算法不能产生一个全家最优的决策树。
• 易于理解和解释，决策树可以可视化