卷积、池化、激活函数、初始化、归一化、正则化、学习率——深度学习基础总结

有幸拜读大佬言有三的书《深度学习之模型设计》,以下是我的读书笔记，仅供参考，详细的内容还得拜读原著，错误之处还望指正。下面的三张图片来自知乎。

《深度学习之模型设计》读书笔记——第二章：深度学习的基础

2.1全连接神经网络的局限性

2.2.1学习原理的缺陷

 传统的机器学习需要人为设计特征描述算子，但人毕竟有限，这从原理上限制了传统全连接神经网络的表达能力，使其只能解决比较简单的问题。

2.2.2全连接神经网络的结构缺陷

• 巨大计算量
• 结构信息的缺失

2.2.3高性能的传统机器学习算法

• Adaboost
• SVM

2.2深度学习第三次复兴简史

2.2.1互联网与大数据来了

 大型数据集的诞生，使很多机器学习模型有了足够多的数据来训练泛化性能足够好的模型。

2.2.2GPU的普及

1.什么是GPU

• 定义：GPU(Graphics Processing Unit)即图形处理器。
• 特点：GPU采用了数量众多的计算单元和超长的流水线，并且省去了Cache。

2.GPU架构与软件平台
 GPU可编程了。
 GPU发展阶段：固定功能架构阶段$\Rightarrow$分离渲染架构阶段$\Rightarrow$统一渲染架构阶段

3.GPU与CPU算力对比
 (1)GPU的浮点运算能力是CPU的十倍以上。
 (2)GPU拥有高速宽的独立显存；浮点运算性能高；几何处理能力强；适合处理并行计算任务；适合进行重复计算；适合图像或视频处理任务；能大幅度降低系统成本。

2.2.3深层神经网络华丽归来

略

2.2.4语音识别的重大突破

略

2.2.5图像识别的重大突破

ZFNet(反卷积)(2013)$\Rightarrow$GoogLeNet(Inception)&VGGNet(2014)$\Rightarrow$ResNet(2015)$\Rightarrow$ResNeXt(分组卷积)&DenseNet(2016)$\Rightarrow$SeNet(2017)

2.2.6自然语言处理的重大突破

LSTM(2014)$\Rightarrow$注意力机制(2014)$\Rightarrow$Transformer(2017)$\Rightarrow$ELMO(2017)$\Rightarrow$GPT(2018)$\Rightarrow$GPT2.0(2019)$\Rightarrow$XLNet(2019)

2.3卷积神经网络基础

2.3.1卷积操作

1.数学上的卷积：

其中$(x\ast w)(t)$称为$x$和$w$的卷积
连续的定义：$(x\ast w)(t)={\int }_{-\infty }^{+\infty }f(\tau )g(t-\tau )d\tau$
离散的定义：$(x\ast w)(t)={\sum }_{-\infty }^{+\infty }f(\tau )g(t-\tau )$

2.二维图形的卷积：

$$(x\ast w)(i,j)=\sum _m\sum _{n}x(m,n)w(i-m,j-n)$$

其中$x$表示输入$w$卷积核。
说白了，卷积就是在图像上滑动，取与卷积核大小相等的区域，逐像素做乘法然后相加。
本人补充：卷积中还有三种模式：
1.full mode

full模式的意思是，从filter和image刚相交开始做卷积，白色部分为填0。filter的运动范围如图所示。
2.same mode

当filter的中心(K)与image的边角重合时，开始做卷积运算，可见filter的运动范围比full模式小了一圈。注意：这里的same还有一个意思，卷积之后输出的feature map尺寸保持不变(相对于输入图片)。当然，same模式不代表完全输入输出尺寸一样，也跟卷积核的步长有关系。same模式也是最常见的模式，因为这种模式可以在前向传播的过程中让特征图的大小保持不变，调参师不需要精准计算其尺寸变化(因为尺寸根本就没变化)。
3.valid mode

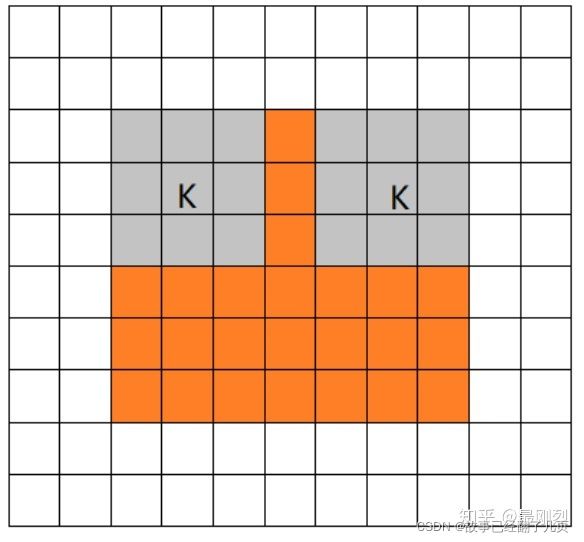
当filter全部在image里面的时候，进行卷积运算，可见filter的移动范围较same更小了。

2.3.2反卷积操作

卷积通常会造成分辨率降低，而反卷积正好相反。
实际上，并没有反卷积这种操作，目前在DeepLearning中主要有两种方式实现反卷积——插值法和转置卷积

1.插值法

已知四个点$Q_{11}=(x_1,y_1),Q_{12}=(x_1,y_2),Q_{21}=(x_2,y_1),Q_{22}=(x_2,y_2)$
对$x$方向进行线性差值:
$f(x,y_1)\approx \frac{x_2-x}{x_2-x_1}f(Q_{11})+\frac{x-x_1}{x_2-x_1}f(Q_{21})$
$f(x,y_2)\approx \frac{x_2-x}{x_2-x_1}f(Q_{12})+\frac{x-x_1}{x_2-x_1}f(Q_{22})$
然后对$y$方向进行线性差值：
$f(x,y)\approx \frac{y_2-y}{y_2-y_1}f(x,y_1)+\frac{y-y_1}{y_2-y_1}f(x,y_2)$
先对y方向再对x方向插值结果一样。

2.转置卷积(反卷积)

实际上也是一种卷积操作，与卷积用相同的代码。
实际运用中，首先计算上采样的倍率($\frac{输出尺寸}{输入尺寸}$)。再根据步长的大小和边界补充的方式对初始输入进行变换。然后使用与卷积一样的方法进行参数学习。

2.3.3卷积神经网络基本概念

1.感受野

在CNN中，是某一层输出结果的一个元素对应的输入层的一个映射，即特征平面上的一个点所对应的输入图像上的区域。
如果一个神经元的大小受到上层$N\times N$的神经元区域的影响，那么就说该神经元的感受野是$N\times N$，因为其反应了$N\times N$区域的信息。

2.池化

实现方式:

1.步长不为1的卷积；
2.直接采样。

池化层可以对输入的特征平面进行压缩，可以：

1.使特征平面变小，简化网络计算复杂度；
2.提取主要特征。

常见的池化有：

Average Pooling、Max Pooling。

2.3.4 卷积神经网络的核心思想

1.稀疏连接

前后层神经元大部分采用局部连接的方式。
思想来源：生理学的感受野机制 和 图像的局部统计特性

2.权值共享

同一个特征平面中的权值共享。
可以使图像局部区域学习到的信息可以应用到其他区域，从而使同样的目标在不同的位置能提取到同样的特征。

3.能建模图像结构信息

空间关系的保留是CNN能提取鲁棒特征的基础

2.3.5 CNN的基本结构配置

• 输入层：包含基础操作：如去均值，灰度归一化
• 卷积层
• 激活层：进行特征的选择和抑制
• 池化层：降低平面的分辨率及抽象特征；压缩网络参数和数据，减小过拟合
• 全连接层
• 损失层；定义损失目标函数(如SGD)，找到最小化损失函数的参数值（损失层的输入是网络的输出和真实的标签）
• 精度层：输入是网络的输出和真实的标签

2.4.1 激活模型与常用激活函数

1.线性模型与阈值模型

2.激活函数

• Sigmoid: $f(x)=\frac{1}{1+e^{-x}}$
• Tanh: $f(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$ 解决了Sigmoid函数的输出值不以0为中心的问题
• ReLU
• Leaky ReLU：$f(x)=max(0.01x,x)$, 解决了Dead ReLU问题，但并未完全证明优于ReLU
• PreLU：将Leaky ReLU中的$\alpha$设置为一个可以学习的参数
• Maxout：$y=max(a_k)=max(w_1^{T}x+b_1,w_2^{T}x+b_2,...,w_n^{T}x+b_n)$ 看作在网络中加入一层激活函数层，其包含一个参数k，特殊在于增加了k个神经元，并输出最大的激活值。
  具有ReLU函数的所有优点 ，没有其缺点。
  能拟合任意的凸函数。
  和Dropout组合使用效果较好。
• Softmax：$f(x_1)=\frac{e^{x_i}}{{\sum }_{k=1}^K{e}^{x_k}}$ 视为Sigmoid的泛化形式。
• Swish：$f(x)=x\ast Sigmoid(\beta x)$ ，是由网络自动搜索出来的激活函数，其中$\beta$是一个可以学习的参数或常数。

3.激活函数的研究方向

1.对ReLU函数负区域进行改进
2.研究不同激活策略对不同的网络层、不同的通道使用的影响
3.使用各类学习方法来对简单的组合进行探索
目前，ReLU函数仍然是最通用的。

2.4.2参数初始化方法

原则：

• 各层激活值不会出现饱和现象
• 各层激活值不为0

理想的初始化：使各层的激活值和状态梯度的方差在传播过程中保持一致

1.初始化为0

不利于优化

2.生成小的随机数

可以用高斯分布
参数的初始值不能太小：较小的参数在传播时会导致过小的梯度产生，对于深层网络而言，会产生梯度弥散。
参数的初始值不能太大：造成振荡，也会使Sigmoid进入梯度饱和区。

3.标准初始化

4.Xavier初始化

5.MSRA初始化

6.初始化方法的使用

• 使用已经训练好的模型（最好的初始化方法）
• 选择更好的激活函数：
  MSRA初始化方法+ReLU系列搭配使用——目前的主流

2.4.3归一化方法

定义：归一化是指将数据约束到固定的分布范围 。

1.Normalization

• 线性对比拉伸：$X=\frac{x-x_{min}}{x-x_{max}}$ ,其中$x_{min}$和$x_{max}$分别是灰度最小值和最大值。
• 直方图均衡化：让一个从随机分布变换到[0,1]均匀分布的变换。
  
  变换步骤：
  
  （1）计算累计概率分布，$cdp(r_k)$表示灰度为 $0-r_k$ 的像素的概率。$cdp(L-1)=1$. $cdp(r_k)={\sum }_{i=0}^{L-1}p(r_k),k=0,1,2...L-1$
  
  （2）创建一个均匀分布，将累计概率分布转换到图像的像素范围，变换关系为：$T(r_k)=round(cdp(r_k)\ast 255+0.5)$，其中$round$表示取整操作。$T(r_k)$在$(0,255)内$
  
  （3）反向映射，变换后新的像素灰度值$y$与原始的像素灰度值$x$的变换关系为$y=T(x)$
• 零均值归一化：处理后数据符合均值为0，标准差为1的标准正态分布。$y_i=\frac{x_i-u}{\delta }$

2.Batch Normalization

通常BN层在卷积层之后，用于重新调整数据分布。

ensp 每个批次的均值：$u_B=\frac{1}{n}{\sum }_{i=1}^n{x}_i$

每个批次的方差：$\delta^2_B = \dfrac{1}{n} \sum^n_{i=1} (x_i-u_B)^2 $

对每个元素进行归一化：$x_i^{{}^{\prime }}=\frac{x_i-u_B}{\sqrt{{\delta }_B^2+\epsilon }}$

尺度缩放和偏移：$y_i={\gamma }_i\times x_i^{{}^{\prime }}+{\beta }_i$, 其中，$\gamma$和$\beta$代表输入数据分布的方差和偏移。

CNN的各个特征维度（通道）之间，是分别进行BN计算的。
BN的好处：1.减轻了对初始值的依赖 2.训练更快，可以使用更高的学习速率
BN的缺点：依赖Batch的大小，当Batch值很小时，计算的均值和方差不稳定。故不适合于1.Batch非常小 2.深度不固定的模型，如RNN

3.Batch Renormalization

BN用每个Batch来代替整体训练集的均值和方差，这要求Batch必须从各类中均匀采样，当Batch值较小时很难满足这一要求。
而Batch Renormalization就可以解决这个问题。
将BN中的对应公式改：
$x_i^{{}^{\prime }}=\frac{x_i-u_B}{{\delta }_{\beta }}.r+d$

其中$r=\frac{{\delta }_{\beta }}{\delta }$, $d=\frac{u_{\beta }-u}{\delta }$

其中$u:=u+\alpha (u_{\beta }-u)$,$\delta :=\delta +\alpha (u_{\beta }-\delta )$

实际使用中，先使用BN将网络训练到一个相对稳定的移动平均值，再使用Batch Renormalization训练。

4.BN变种

• Layer Normalization(LN)：适用于RNN等时序模型
• Instance Normalization(IN)：适用于图像生成及风格迁移
• Generalized Normalization(GN)：适用于Batch较小
• Switchable Normalization(SN):在包含归一化方法的池中进行选择，然后用精度进行比较择优，最终在任务中自适应地学习出最佳配置。具体结果可能是：当批处理越小时，BN越不稳定，其对应权重系数越小，IN和LN的权重系数则越大；反之BN的权值系数越大（有点像随机森林）。

2.4.4池化

1.基于手动设计池化的方案

• Average Pooling
• Max Pooling
• Mixed Pooling：在Average Pooling和Max Pooling中进行随机选择，可提供一定的正则化能力
• Stochastic Pooling：对feature map中的元素按照概率值的大小随机选择，元素被选中的概率与其数值大小正相关。

2.基于数据驱动的池化方案

正在研究中

3.池化机制的理解

作用：在一定程度上增加了平移不变性
对深层的网络并没有起到太大的作用，真正有用的是数据增强操作。

2.4.5最优化方法——优化器

• SGD(Stochastic Gradient Descent)：每次只选取一个样本进行梯度计算
• RMSProp
• AdaGrad
• NAG(Nesterov Accelerated Gradient)
• Adam:本质上是带有动量项的REMSProp
• Adamax：对学习率的上限提供了更简单的范围
• Nadam：带有Nesterov动量项的Adam
• 牛顿法
• 拟牛顿法
• 共轭梯度法

2.4.6学习率策略

越在训练后期，学习率越小，有助于收敛的稳定

• Fixed：固定学习率策略
• Step：按照指定步长对学习率进行调整。如：学习率每经过10000次迭代后降低为原来的0.1倍
• Multistep：非均匀步长降低策略
• Exp：指数变化策略
• Inv：另一种指数变化策略
• Poly：另一种指数变化策略
• Sigmoid

2.4.7正则化方法

1.过拟合和欠拟合

• 过拟合(Overfitting)：数据集很小 或 模型太大 ——解决方法：正则化和数据扩充
• 欠拟合(Underfitting)：没有训练充分

2.正则化

• 正则化(Regularization)：目标：让经验风险和模型复杂度同时较小。作用：以增大训练集的误差来减小泛化误差。

3.提前停止

验证误差不再增大后，提前结束训练
充分利用训练数据集的策略：1.将全部训练数据一起训练固定的迭代次数 2.迭代训练流程，直到训练误差小于提前停止策略设置的验证误差。

4.模型集成

• Model Ensemble Methods:通过合并多个模型的结果来得到更好的模型
• dropout

5.参数惩罚

6.训练样本扩充

• CV中：对图片旋转、缩放、平移等
• NLP中：近义词替换等
• 语音识别中：添加随机噪声等