python学习笔记五(函数基础)
博主在学完python基本数据类型后就开始迫不及待的去编写自己的程序去了,但是写出来的程序总是和大神的差了不是一星半点,后来发现那是因为我和大神之间差了n个函数w(゚Д゚)w,因此勤学努力的博主又去学习了帮助python高逼格编程的函数^_^
函数定义
python 定义函数的格式如下:
def function_name(形参列表):
function_body
return value
举个简单的栗子
def mymax(a,b):
if a>b:
return a
return b从上面的定义引出了关于理解函数的一系列问题:参数传递、形参定义、变量定义。来让我们继续自己的装逼之路(▼へ▼メ)
函数形参定义
不论是哪种编程语言形参的定义规则总是让人很头痛,python由于没有指针概念因此在定义形参的过程中更是让人痛苦,
python形参的类型可以总结为五种
- 缺省参数
- 位置形参
- 星号元组形参
- 命名关键字形参
- 双星号字典形参
缺省参数
缺省定义:缺省参数一般是为了占位的形参设置默认值,一旦创建就一直存在
创建规则:
缺省参数必须自右至左依次存在,一旦出现缺省参数,那么其后的参数也必须是缺省参数
举个栗子如下
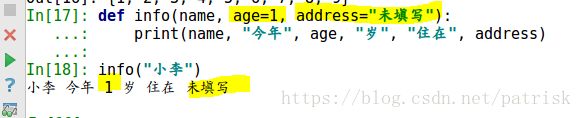
def info(name,age =1,address = "未填写")
print(name,"今年",age,"岁","住在",address)
info("小李")位置形参
定义:根据形参位置确定形参的传入值
创建规则:
def function_name(形参1,形参2,形参3,...)
举个栗子如下:
def mymax_byteacher_a(a,b):
#经典算法:求出最大值,用变量保存
max_number = a
if b >max_number:
max_number = b
#将最大值返回
return max_number其中a,b就是典型的位置形参,但是如果传入的参数十分多的话位置形参定义就会显得十分繁琐比如
def fa(a,b,c,d,e,f):
pass
再如果我们并不知道要传入多少个参数,这时位置形参就不够了,emmm,我们需要位置形参的升级定义模式--->星号元祖形参
星号元祖形参
如上所述,这是位置形参的升级版,最大的作用就是用来收集多余的位置形参,一般情况下一个函数中只有一个元组形参,就像一个台电脑只需要一个垃圾回收站
定义规则:
def 函数名(*元祖形参名):
语句块
让我再举个栗子如下:
def fb(*args):
#args 绑定一个元祖
print("实参个数是:",len(args))
print("args=",args)
不论是使用基础的位置形参定义还是高级的星号元组形参定义模式都要面临一个比较烦的问题,就是你一定要记住自己每个参数的传入顺序,对于一些代码的后期阅读和修复都是极为不友好的因此python又引入了一种形参定义方式命名关键字形参
命名关键字形参
定义规则:
def 函数名(*,命名关键字形参):
语句块
def 函数名(*args,命名关键字形参):
语句块
来吧我们再举一个栗子٩꒰▽ ꒱۶⁼³₌₃
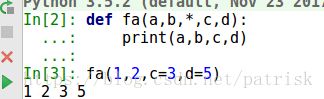
def fa(a,b,*,c,d):
print(a,b,c,d)
fa(1,2,c=4,d=5)
#这里的*用来标志位置形参的结束和,命名关键字形参的开始def fb(a,b,*args,c,d):
print(a,b,args,c,d)
fb(1,2,3,4,5,c=6.d=7)
#这里的*args是位置形参里面用来收集多余形参的元组通过命名关键字形参我们可以明确的知道自己定义的形参意义,在调用过程中也可以明白实参到底传给哪个形参了,但是这里也有一个问题如果有多了形参,或者不明确传入形参个数的情况下,我们需要命名关键字形参的升级版本—->双兴号字典形参
双星号字典形参
定义规则:
def 函数名(**字典形参名):
函数体
用于收集多余的关键字传参
让我呢再举一个栗子如下:
def fc(*kwargs):
print("多余关键字传参的个数",len(kwargs))
print("kwargs = ",kwargs)
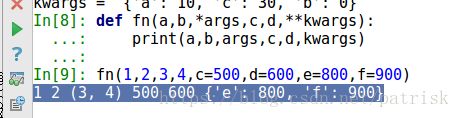
fc(a=10,b=20,c=30)def fn(a,b,*args,c,d,**kwargs):
print(a,b,args,c,d,kwargs)
fn(1,2,3,4,c=500,d=600,e=800,f=900)函数参数传递
既然上面我们已经定义好了函数和形参,那么下一步就需要将我们要处理的数据传入函数进行处理了,下面开始进行python参数传递,可想而知参数传递的形式肯定和上面类似,就像跑道都画好了,你就上档开始加速啊ヽ( ̄▽ ̄)ノ
- 位置传参
- 序列传参
- 命名关键字传参
- 字典关键字传参
位置传参
序列传参对应位置形参定义,实参的传递与形参的位置对应举个栗子
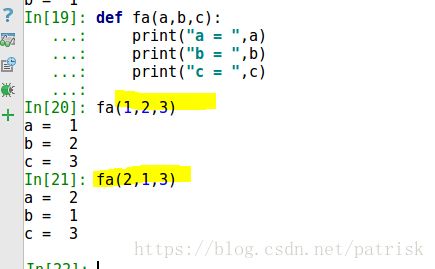
def fa(a,b,c):
print("a = ",a)
print("b = ",b)
print("c = ",c)
fa(1,2,3)
fa(2,1,3)序列传参
传参时如果有多个参数一起传入,比如传入一个列表,此时需要将列表拆分为单个数据对应为每个位置的形参,能够实现这个操作的就是–>序列传参
举个栗子
L = [1,2,3]
fa(*L)
注意:这里要传入的序列的长度必须与定义的形参个数相同,如果不同就会出现错误如下:

那么新的问题来了,如果我们不知道自己传入的参数有多少个该怎么办呢?请返回上面的星号元组形参的定义,让星号元组形参定义和序列传参相结合那么,python的函数的参数你想怎么传就怎么传!!!!!(ノ=▼ω▼=)ノ┴─┴再一次举栗子:
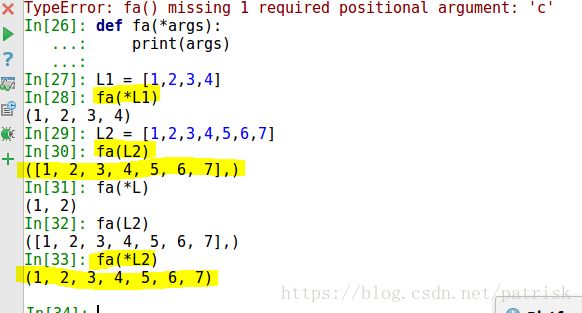
def fa(*args):
print(args)
L1 = [1,2,3,4]
L2 = [1,2,3,4,5,6,7]
L = [1,2]
fa(*L1)
fa(L2)
fa(*L)
fa(*L2)关键字传参
参数法传递时根据命名关键进行匹配与形参位置无关
def fa(a,b,c)
print("a = ",a)
print("b = ",b)
print("c = ",c)
fa(a=1,b=2,c=3)
这里有一个问题需要说明:如果用位置形参形式定义的形参那么在实参传递过程中可以使用位置传参、序列传参、关键字传参,但是如果使用命名关键定义的形参形式传参过程中只能使用关键字传参。
字典关键字传参
指传入的实参为字典,那么根据字典键值与形参关键字匹配进行传参,举一个栗子
def fb(a,b,c):
print("a = ",a)
print("b = ",b)
print("c = ",c)
d = {"a":111,"c":333,"b":222}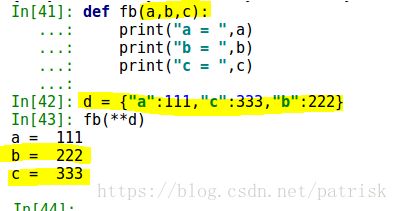
此时我们又遇到了和位置传参相同问题了如果不知道我要传入多少个参数呢?那么请你返回上面看一下双星号字典形参定义,话不多说,我们还是把栗子拿出来吧\\\٩(‘ω’)و////
def fa(**kwargs):
print(kwargs)
d1 = {"key1":1,"key2":2}
d2 = {"key1":1,"key2":2,"key3":3,"key4":4}
fa(**d1)
fa(**d2)
至此关于函数参数的问题目前看来已经结束了,那让我们继续看返回return吧(✧◡✧)
函数返回
python的返回是我见过最强大的就是你想怎么返回就怎么返回想返回几个就返回几个,只不过在接收返回参数的过程中需要和返回时数据的顺序一致
#返回两个列表
def split_numbera_a(L):
odds = list()
evens = list()
for i in L:
if i%2 == 0:
evens.append(i)
else:
odds.append(i)
return odds,evens
L=[1,2,3,4,5,6,7]
odds,evens =split_numbera_a(L)
odds
evens
evens,odds =split_numbera_a(L)
odds
evens
#返回一个字典
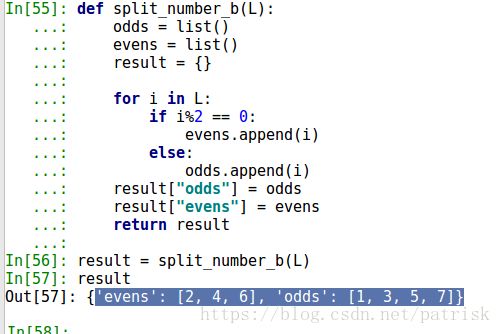
def split_number_b(L):
odds = list()
evens = list()
result = {}
for i in L:
if i%2 == 0:
evens.append(i)
else:
odds.append(i)
result["odds"] = odds
result["evens"] = evens
return result
result = split_number_b(L)#返回一个字符串
def myprint(*args,sep = ' ',end="\n"):
L =[str(x) for x in args]
s = sep.join(L)
s += end
return s
s = myprint(1,2,3,4,sep="//",end="\n")
至此关于python3 的函数基础基本上已经总结完成,少年开始快乐的python3编程了
ε=ε=ε=ε=ε=ε=┌(; ̄◇ ̄)┘