笔记——迭代法之雅可比算法

迭代法

迭代法（Iterative Method）是一种最常使用求解大型、稀疏线性方程组的方法，与直接法相比，它具有方法简单，存储空间小（迭代法通常只对系数矩阵中的非零元素进行运算）等优点，特别是在有限步内无法得到问题的解时，迭代法就可在有限的迭代步数后，停止运算而得到足够好的近似解。

雅可比迭代法

它是一种最简单的线性方程组的迭代解法。并且很适合于并行化，每次迭代均使用上次迭代的值。
SISD上雅可比迭代法：对于求解线性方程组 Ax=b，未知向量 x 的分量可写成如下形式∶

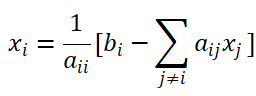
雅可比迭代原理是，使用第 k-1步所计算的变量 xi(k-1)，来计算第k步的xi(k)值：

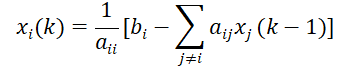
偏微分方程的差分解法——试考虑拉普拉斯方程的第一边值问题（狄利克雷问题）：

（狄利克雷边界条件，为常微分方程的“第一类边界条件”，指定微分方程的解在边界处的值。求出这样的方程的解的问题被称为狄利克雷问题。）

其中，μ(x,y)为有界区域D的边界S上的已知函数。为了求解此偏微分方程，我们可以用差商代替偏导数，得到相应的差分方程，通过解差分方程就可得到偏微分方程的近似解，转化为代数问题。

试考虑在平面(x,y)上一个以 S为边界的有界区域D上定解问题。为了用差分法求解，可以分别作平行x 轴和y轴的直线簇xi=id , yj=jd (i,j=0,1,…,n;d为步距)，从而构成一个等间距正方网格，面直线的诸交点(xi,yj)称为格点，记之为(i,j)。当i,j=1,2,…,n-1时的格点称为内格点，在S上的格点称为边界格点。所有内格点上，函数u(x,y)的偏导数可用差商代替∶

（差商即均差，一阶差商是一阶导数的近似值。对等步长(h)的离散函数f(x)，其n阶差商就是它的n阶差分与其步长的n次幂的比值。例如n=1时，若差分取向前的或向后的，所得一阶差商就是函数的导数的一阶近似；若差分取中心的（xi+d;xi;xi-d）（中心差分法），则所得一阶差商是导数的二阶近似。）

若格点(i,j)处的函数u(x,y)记之为uij，且取d=1，则（10.12）式可简化为∶

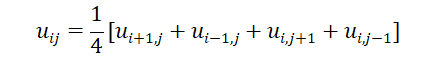
它就是有名的五点格式，即任一格点(i,j)上uij的值等于周围相邻四格点上解的值的算术平均。
使用雅可比算法求解该方程，照例使用第k-1步所计算的变量来计算第k步的变量，通过迭代计算出该方程的解。

串行实现

#include 
#include 
#include 
#include "mpi.h"
#define N 131072LL
int main(int argc, char *argv[]){
    double *myRows=(double*)malloc(sizeof(double)*N*N);
    double *myRows2=(double*)malloc(sizeof(double)*N*N);
    int myid;
    double diffval=0;
    double tempdata=0;
    double start_time=0;
    double end_time=0;
    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &myid);
    start_time=MPI_Wtime();
    int i,j;
    /*初始化*/
    for (i = 0; i< N; i++){
        for ( j = 0; j<N; j++){
            if(i==0||i==N-1||j==0||j==N-1){
                myRows[i*N+j] = 8.0;
                myRows2[i*N+j] = 8.0;
            } 
            else{
                myRows[i*N+j] = 0;
                myRows2[i*N+j] = 0;
            }
        }
    }
    /*Jacobi Iteration部分*/
    int step;
    double diff=2;
    while(diff > 0.5){
        // 计算
        diff = 0;
        for ( i = 1; i<N-1; i++){
            for ( j = 1; j<N-1; j++)
                myRows2[i*N+j] = 0.25*(myRows[i*N+j-1]+myRows[i*N+j+1]+myRows[(i-1)*N+j]+myRows[(i+1)*N+j]);
        }
        // 更新
        for ( i = 0; i< N ; i++){
            for (j = 0; j< N; j++){
                diffval=fabs(myRows2[i*N+j]-myRows[i*N+j]);
                diff = fmax(diffval,diff);  /
                myRows[i*N+j] = myRows2[i*N+j];
            }
        }
        // printf("the value is %lf\n",diff);   
    }
    // 结果矩阵输出
    // for (i = 0; i< N; i++){
    //     for ( j = 0; j
    //         printf("%lf ",myRows[i*N+j]);
    //     }
    //     printf("\n");
    // }
    end_time=MPI_Wtime();
    MPI_Finalize();
    printf("chuanxing total time is %lf\n",end_time-start_time);
    free(myRows);
    free(myRows2);
}
// mpicc A.c -o A -lm（需链接math.h)
// mpirun ./A

MPI分行实现

将矩阵按行均分为四块，每块要增加两行分别存放与相邻两块通信交换得来的数据。将四块数据分别交于四个进程进行计算，每次计算前要进行进程间通信，交换边界数据。

#include 
#include 
#include 
#include "mpi.h"
#define N 131072LL
#define SIZE N/4
#define T 3          
#define RANKSIZE 4   //使用进程数量
//雅可比mpi分行并行加测试时间
int main(int argc, char *argv[]){
    // double myRows[SIZE+2][N], myRows2[SIZE+2][N];//使用动态构建，便于扩大规模测试
    double *myRows=(double*)malloc(sizeof(double)*(SIZE+2)*N);
    double *myRows2=(double*)malloc(sizeof(double)*(SIZE+2)*N);
    // double diffs[RANKSIZE+1];
    // double comtime[RANKSIZE+1];
    // double multime[RANKSIZE+1];
    double *diffs=(double*)malloc(sizeof(double)*(RANKSIZE+1));
    double *comtime=(double*)malloc(sizeof(double)*(RANKSIZE+1));
    double *multime=(double*)malloc(sizeof(double)*(RANKSIZE+1));
    double comtimeto=0;
    double multimeto=0;
    double comt=0;
    double mult=0;
    double tempcomtimeto=0;
    double tempmultimeto=0;
    int myid;
    int temp = 1;
    double diffval=0;
    double tempdata=0;
    double start_time=0;
    double mid1_time=0;
    double mid2_time=0;
    double end_time=0;
    MPI_Status status;
    MPI_Init(&argc, &argv);
    MPI_Comm_rank(MPI_COMM_WORLD, &myid);
    MPI_Barrier(MPI_COMM_WORLD); //保证进程开始计时时间一样，不受进程启动时间不同的影响
    start_time=MPI_Wtime();
    int i,j;
    /*初始化*/
    for ( i = 0; i<SIZE+2; i++){
        for ( j = 0; j<N; j++){
            myRows[i*N+j] = myRows2[i*N+j] = 0;
        }
    }
    if ( myid == 0) {
        for ( j = 0; j<N; j++)
            myRows[1*N+j] = 8.0;
    }
    if (myid == 3) {
        for ( j=0; j<N; j++)
            myRows[SIZE*N+j] = 8.0;
    }
    for ( i = 1; i<SIZE+1; i++){
        myRows[i*N+0] = 8.0;
        myRows[i*N+N-1] = 8.0;
    }
    /*Jacobi Iteration部分*/
    int step;
    double diff=2;
    //for ( step = 0; step < T; step++ ){
    while(diff > 0.5){//通过设置收敛条件来控制迭代次数
        // MPI_Barrier(MPI_COMM_WORLD); 
        // start_time=MPI_Wtime();
        // 传递数据             ！
        if (myid<3) {
            // 从 下方 进程接收数据
            MPI_Recv(&myRows[(SIZE+1)*N+0], N, MPI_DOUBLE, myid+1, 0, MPI_COMM_WORLD, &status);
        }
        if (myid>0) {
            // 向 上方 进程发送数据
            MPI_Send(&myRows[1*N+0], N, MPI_DOUBLE, myid-1, 0, MPI_COMM_WORLD);
        }
        if (myid<3) {
            // 向 下方 进程发送数据
            MPI_Send(&myRows[SIZE*N+0], N, MPI_DOUBLE, myid+1, 0, MPI_COMM_WORLD);
        }
        if (myid>0) {
            // 从 上方 进程接收数据
            MPI_Recv(&myRows[0], N, MPI_DOUBLE, myid-1, 0, MPI_COMM_WORLD, &status);
        }
        //测量通信时间
        // MPI_Barrier(MPI_COMM_WORLD); 
        // mid1_time=MPI_Wtime();
        // comt=mid1_time-start_time;
        // MPI_Gather(&comt, 1, MPI_DOUBLE, comtime, 1, MPI_DOUBLE , 0, MPI_COMM_WORLD);
        // if (myid==0) {
        //     tempcomtimeto=comtime[0];
        //     for (int w = 1; w < RANKSIZE; w++){
        //         if(comtime[w]>comtime[w-1])
        //             tempcomtimeto=comtime[w];
        //     }
        //     // printf("the tempcomtimeto is %lf\n",tempcomtimeto);
        //     comtimeto+=tempcomtimeto;
        //     printf("the comtimeto is %lf\n",comtimeto);   
        // }
        // MPI_Barrier(MPI_COMM_WORLD); 
        // mid2_time=MPI_Wtime();
        // 计算
        diff = 0;
        int r_begin, r_end;
        r_begin = (myid==0) ? 2 : 1;
        r_end = (myid==3) ? SIZE-1 : SIZE;
        for ( i = r_begin; i<=r_end; i++){
            for ( j = 1; j<N-1; j++)
                myRows2[i*N+j] = 0.25*(myRows[i*N+j-1]+myRows[i*N+j+1]+myRows[(i-1)*N+j]+myRows[(i+1)*N+j]);
        }
        // 更新
        for ( i = r_begin; i<=r_end; i++){
            for (j = 1; j<N-1; j++){
                diffval=fabs(myRows2[i*N+j]-myRows[i*N+j]);
                diff = fmax(diffval,diff);  //还要传回主进程进行判断
                myRows[i*N+j] = myRows2[i*N+j];
            }
        }
        //测量计算和更新时间
        // MPI_Barrier(MPI_COMM_WORLD); 
        // end_time=MPI_Wtime();
        // mult=end_time-mid2_time;
        // MPI_Gather(&mult, 1, MPI_DOUBLE, multime, 1, MPI_DOUBLE , 0, MPI_COMM_WORLD);
        // if (myid==0) {
        //     tempmultimeto=multime[0];
        //     for (int w = 1; w < RANKSIZE; w++){
        //         if(multime[w]>multime[w-1])
        //             tempmultimeto=multime[w];
        //     }
        //     // printf("the tempmultimeto is %.9lf\n",tempmultimeto);
        //     multimeto+=tempmultimeto;
        //     printf("the multimeto is %.9lf\n",multimeto);   
        // }
        // printf("here is the %d , the diff is %lf.\n",myid,diff);
        MPI_Barrier(MPI_COMM_WORLD);
        MPI_Gather(&diff, 1, MPI_DOUBLE, diffs, 1, MPI_DOUBLE , 0, MPI_COMM_WORLD);
        if (myid==0) {
            tempdata=diffs[0];
            for (int w = 1; w < RANKSIZE; w++){
                if(diffs[w]>diffs[w-1])
                    tempdata=diffs[w];
            }
            diff=tempdata;
            printf("the value is %lf\n",diff);   
        }
        MPI_Bcast(&diff,1,MPI_DOUBLE,0,MPI_COMM_WORLD);//必须有
    }
   // MPI_Barrier(MPI_COMM_WORLD);

    // 结果输出
    // if ( myid>0 ) {
    //     MPI_Recv(&temp, 1, MPI_INT, myid-1, 0, MPI_COMM_WORLD, &status);
    // }
    // printf("Result in process %d:\n", myid);
    // for ( i = 0; i
    //     for ( j = 0; j
    //         printf("%1.3f\t", myRows[i*N+j]);
    //     printf("\n");
    // }
    // if ( myid<3 ) {
    //     MPI_Send(&temp, 1, MPI_INT, myid+1, 0, MPI_COMM_WORLD);
    // }

    MPI_Barrier(MPI_COMM_WORLD);  //保证计时
    end_time=MPI_Wtime();
    MPI_Finalize();
    // printf("time is %lf\n",end_time-start_time); //所有进程都会执行
    // if(myid==0){
    //     printf("Communication accounted for %lf\n",comtimeto/(comtimeto+multimeto));
    //     printf("Calculation accounted for %lf\n",multimeto/(comtimeto+multimeto));
    // }
    if(myid==0)
        printf("total time is %lf\n",end_time-start_time);
}

可以通过这个程序测试计算和通信占比：（由于设备问题，只使用了一个结点）

N=100000	时间	占比
通信	0.0132s	0.008%
计算	164.7896s	99.992%

MPI分块实现

虚拟拓扑：
虚拟拓扑可以用图来表示，结点代表进程，边用来连接彼此之间通信的进程。目前应用最多的是具有规则的网格形状的笛卡尔拓扑。
Jacobi解决狄利克雷问题，使用笛卡尔拓扑，划分为2*2的网格。按行列同时划分时，分块数组需要和上下左右的邻居同时通信，为此，分块数组的上下左右都预留出需要通信的部分，用来存放同各个方向邻居通信得到的数据。

#include "mpi.h"
#include 
#include 
#include 
#define arysize 131072LL  //2的十七次方
#define arysize2 (arysize/2)
int main(int argc, char *argv[]){
    int n, myid, numprocs, i, j, nsteps=6;
    double *a=(double*)malloc(sizeof(double)*(arysize2+2)*(arysize2+2));
    double *b=(double*)malloc(sizeof(double)*(arysize2+2)*(arysize2+2));
    // double a[arysize2+2][arysize2+2],b[arysize2+2][arysize2+2];/*定义局部数组的大小 包含边界空间*/
    double starttime,endtime;
    int col_tag,row_tag,send_col,send_row,recv_col,recv_row;
    int col_neighbor,row_neighbor;
    MPI_Comm comm2d;
    MPI_Datatype newtype;
    int right,left,down,top,top_bound,left_bound,down_bound,right_bound;
    int periods[2];
    int dims[2],begin_row,end_row;
    MPI_Status status;
    MPI_Init(&argc,&argv);
    dims[0] = 2;
    dims[1] = 2;
    periods[0]=0;
    periods[1]=0;
    MPI_Cart_create( MPI_COMM_WORLD, 2, dims, periods, 0,&comm2d);/*定义虚拟进程拓扑 它是一个2´ 2的网格 得到的包含进程拓扑信息的新的通信域是comm2d*/
    MPI_Comm_rank(comm2d,&myid);
    MPI_Type_vector( arysize2, 1, arysize2+2,MPI_DOUBLE,&newtype);/*定义向量数据类型来表示一列*/
    MPI_Type_commit( &newtype );/*新类型的递交*/
    MPI_Cart_shift( comm2d, 0, 1, &left, &right);/*得到当前进程左右两侧的进程标识*/
    MPI_Cart_shift( comm2d, 1, 1, &down, &top);/* 得到当前进程上下方的进程标识*/
    /*下面的程序为数组赋初值*/
    for(i=0;i<arysize2+2;i++) 
        for(j=0;j<arysize2+2;j++) 
            a[i*(arysize2+2)+j]=0.0;
    if (top == MPI_PROC_NULL){
        for ( i=0;i<arysize2+2;i++) 
            a[1*(arysize2+2)+i]=8.0;
    }
    if (down == MPI_PROC_NULL){
        for ( i=0;i<arysize2+2;i++) 
            a[arysize2*(arysize2+2)+i]=8.0;
    }
    if (left == MPI_PROC_NULL){
        for ( i=0;i<arysize2+2;i++) 
            a[i*(arysize2+2)+1]=8.0;
    }
    if (right == MPI_PROC_NULL){
        for ( i=0;i<arysize2+2;i++) 
            a[i*(arysize2+2)+arysize2]=8.0;
    }
    col_tag = 5; row_tag = 6;
    printf("Laplace Jacobi#C(BLOCK,BLOCK)#myid=%d#step=%d#total arysize=%d*%d\n",myid,nsteps,arysize,arysize);
    top_bound=1;
    left_bound=1;
    down_bound=arysize2;
    right_bound=arysize2;
    if (top == MPI_PROC_NULL) top_bound=2;
    if (left == MPI_PROC_NULL) left_bound=2;
    if (down == MPI_PROC_NULL) down_bound=arysize2-1;
    if (right == MPI_PROC_NULL) left_bound= arysize2-1;
    MPI_Barrier(MPI_COMM_WORLD);
    starttime=MPI_Wtime();
    for (n=0; n<nsteps; n++) {
        MPI_Sendrecv( &a[1*(arysize2+2)+1], arysize2, MPI_DOUBLE, top, row_tag,& a[(arysize2+1)*(arysize2+2)+1],arysize2, MPI_DOUBLE, down, row_tag, comm2d, &status );/*向上数据传送*/
        MPI_Sendrecv( &a[arysize2*(arysize2+2)+1], arysize2, MPI_DOUBLE, down, row_tag,& a[0*(arysize2+2)+1],arysize2, MPI_DOUBLE, top, row_tag, comm2d, &status );/*向下数据传送*/
        MPI_Sendrecv( &a[1*(arysize2+2)+1], 1,newtype, left, col_tag,& a[1*(arysize2+2)+arysize2+1], 1, newtype,right, col_tag, comm2d, &status );/*向左数据传送*/
        MPI_Sendrecv( &a[1*(arysize2+2)+arysize2], 1, newtype, right, col_tag, &a[1*(arysize2+2)+0], 1, newtype, left,col_tag, comm2d, &status );/*向右数据传送*/
        for ( i=left_bound;i<right_bound;i++) 
            for (j=top_bound;j<down_bound;j++)
                b[i*(arysize2+2)+j] = (a[i*(arysize2+2)+j+1]+a[i*(arysize2+2)+j-1]+ a[(i+1)*(arysize2+2)+j]+a[(i-1)*(arysize2+2)+j])*0.25;
        for ( i=left_bound;i<right_bound;i++) 
            for (j=top_bound;j<down_bound;j++)
                a[i*(arysize2+2)+j] = b[i*(arysize2+2)+j];
    }
    MPI_Barrier(MPI_COMM_WORLD);
    endtime=MPI_Wtime();
    if(myid==0)
        printf("131072LL elapse time=%f\n",endtime-starttime);
    MPI_Type_free( &newtype );
    MPI_Comm_free( &comm2d );
    MPI_Finalize();
}

划分格式如图：

串行、分行、分块运行时间对比

N=131072	时间
串行	1332.307798s
分行	316.368530s
分块	271.883872s