CV笔记7：计算机视觉的通俗理解

目录

一、图像处理与计算机视觉

1.1 PhotoShop与图像处理

1.2 图像处理【实质+常见方法】

1.3 计算机视觉比图像处理区别在哪里

二、通俗理解计算机视觉决策流程

2.1 流程的简单实现

2.2 feature提取

2.3 model

2.4 决策性的result

2.5 小结

补充

图像灰度直方图 --> 对图像统计方面的描述

---

 

一、图像处理与计算机视觉

1.1 PhotoShop与图像处理

ps就是封装好的图像处理的算法，用一个软件形式进行展示并操作。

1.2 图像处理【实质+常见方法】

在使用opencv等工具进行处理时，其实就是将图像看成了矩阵，即图像就是矩阵，而图像处理就是对矩阵的处理。例如图像中的灰度图就是M×N的矩阵，彩色图就是M×N×3的图片。不仅仅是图像处理中将图像看作为矩阵，在计算机视觉中也是如此。我们可以回忆一下，在我们常熟悉的图像处理的方法有：颜色空间、仿射变换，投影变换、卷积、梯度、灰度均值化、直方图、直线检测（圆检测）等，这些也都是针对矩阵进行的。

1.3 计算机视觉比图像处理区别在哪里

我们经常讲到计算机视觉和图像处理。但两者的差别在哪里呢？我们看下他们的输入和输出：

图像处理：输入matrix --> 输出matrix

计算机视觉：输入matrix list --> 输出决策性的结果

所以，我们可以看到，计算机视觉加上了一些机器学习、深度学习等人工智能的东西在里面。因此我们也可以说：图像处理 + 机器学习 = 计算机视觉。

二、通俗理解计算机视觉决策流程

计算机视觉其实可以总结为如下的流程：

输入image --> 提取feature --> model（train&predict） --> 决策性result

2.1 流程的简单实现

上面我们给出了计算机视觉的实现流程，下面我们使用一个简单的例子进行整体流程的简要讲解。

假设我们有10张6×6的数字图片分别为1-10（像素值为0或1），其数字“8”和“1”的形式如下所示：

我们要做的就是使用某种方式能够将图像中的数据进行识别。

最简单的方式就是我们可以将上面6×6的图像数据的每行数据拼接转变成1×36的向量，而这个向量也就是我们需要的feature。

然后我们使用标准图像(假设提前规定好的某一6×6数字图像)的1×36的向量减去待预测图像的1×36向量，计算出来这两者的差值。如果差值为0，说明待预测的图像正是现在与其相减的数字；如果差值不为0说明待预测的图像不是现在与其相减的数字。上面这一相减并判断的过程，我们可以将其数学化为一个函数f(x)，当我们输入一个x，即1×36的向量时，我们便能够知道f(x)的值，也就是该对应图像到底时数字几。这个f(x)就是我上面提到的model，又称为判别器，f(x)的值就是所说的决策性的结果。

2.2 feature提取

在上面的例子中，我们将6×6的图像数据转变成1×36的向量，并应用在了后面的模型中。这个1×36的向量的其实就是我们提取的一种特征。假如，我们将上面的数字“8”旋转180°，作为一个新的图像：

这时仍然将图像转换成1×36的向量，我们可以很明确的知道现在的向量与之前的向量是不一样的。再用上面提到的f(x)进行计算，我们的就不能正确的得到该数字为“8”的结果。我们再怎么做呢？下面提出两种思路，虽然各有不足，但是都能够让我们理解特征提取过程和目的。

第一个方法：可以使用直方图向量作为新的特征x用来训练模型并预测。（灰度直方图可以参见本文补充部分）

这个地方强调一下，此时的x就是我们后续model的输入参数，和上面提到的x为1×36的向量道理一样，只不过是特征变了。我们在使用直方图向量时，无论图像中的数字是否旋转，还是发生了位置的变化，甚至图像尺寸发生了变化，但该数字的直方图向量是不会变化的。这时我们再用f(x)去判别图像到底为数字几。但是使用直方图特征也会存在缺陷，例如有两个数字的直方图向量相同，那么我们就很难正确的判断出该数字。

第二个方法：我们将二维图像的像素值向低维方向做投影，作为新的特征x。

还是以数字“8”为例，我们将图像像素值个数统计向x轴上进行映射，我们可以得到向量x=(0, 2, 3, 2, 0)。如下图：

这时候我们就可以使用这个投影向量x=(0, 2, 3, 2, 0)作为新的特征来描述数字“8”.对于其他的数字同样处理即可。同样的，我们将这个投影向量再带到后面的model中进行数字的判断就完成了整个数字识别流程。

我们看到，我们已经实现了3种特征的提取：①像素直接拼接；②直方图向量做特征；③投影向量。我们也从中发现一些特征在图像发生位置变化的时候其值是不会改变的，这些我们就称为特征的位置不变性。同理的，还有旋转不变性、光照不变性等。我们之所以提取这些不同的特征，就是为了能够使模型更好的来检测或识别出图像种的数字。

2.3 model

模型就是通过输入提取出的特征，用来判别图像到底为数字几（此处为分类）的一种算法。就如上面我们使用的待预测图像和标准图像的1×36向量相减一样，其实就是一种算法，该算法相当于求出了两个向量之间的差异(或相似度)。但是，这仅仅是一种很简单的算法，我们还可以将其换做其他的方法。

我们可以求带预测图像特征和标准图像特征的欧氏距离，并判断待预测图像与哪个数字特征的欧氏距离最小，最小的欧氏距离对应的数字就是待预测图像的数字。这样我们就进一步强化了模型。我们也可以利用一些已经存在的模型进行判断，如SVM，CNN等。

2.4 决策性的result

如上面的案例，输出的结果一个表征图像类别的数字。除此之外，决策性的result还可能是图片中某个物体的位置，精细轮廓，一句话的描述等。其分别针对着计算机视觉中的四大类问题：

• 分类问题
• 检测问题
• 分割问题
• 描述问题

2.5 小结

我们通过上面的例子介绍了计算机视觉的基本流程：

输入image --> 提取feature --> model（train&predict） --> 决策性result

从这个流程我们也能够看出为什么说计算机视觉是图像处理+人工智能：有一些的图像的特征都是图像处理中的基本概念和知识，我们使用图像处理后的matrix作为后续model的输入进而实现图像的分类或识别。在这个过程中，当我们的提取的feature具有良好的性质，能稳健地描述图像时，我们的model是可以使用简单一点的。同样的，当model很强时，则feature就可以弱一些，甚至都不需要feature。在现在的一些深度学习的算法中，通常会将特征提取和分类统一在了model之中，这并不是意味着没有特征提取。例如，当一个神经网络提取特征的时候能够直接提取到一个数字，其实我们就能够将这一个数字认为是我们需要的分类结果，这个过程我们仍可以称为是特征提取过程，只不过是超强的特征提取器。

 

补充

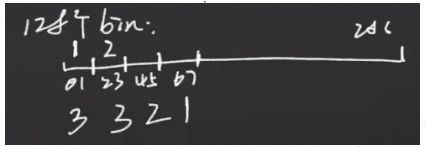
图像灰度直方图 --> 对图像统计方面的描述

 

简单理解，图像的灰度直方图即对规定bin的图像灰度值的统计个数。如上图中左上角的3×3的图像，在bin=256的情况下，0-255像素值的统计个数如图上所示，这个由表示各像素值个数的向量我们变成为该3×3图像的直方图向量。而直方图就是将该向量使用直方图进行了表示。上面我们提到了bin，bin可以理解为分成了多少个盛装相邻灰度值的桶。如上图，我们bin=256，就能理解为在0-255灰度值范围内，相当于每一个灰度值占用一个bin。若我们将上面的图像求解灰度直方图的时候规定bin=128，就相当于没两个相邻像素占用一个bin。如下图：