吴恩达机器学习第六周学习笔记及编程作业答案

一、理论基础
1. 评估一个假设
为了检验算法是否过拟合，我们将数据分成训练集和测试集，通常用 70%的数据作为训练集，用剩下 30%的数据作为测试集（训练集和测试集均要含有各种类型的数据，所以要对数据进行“洗牌”，然后再分成训练集和测试集）。
2. 模型选择和交叉验证集
使用交叉验证集来择一个更能适应一般情况的模型，即：使用 60%的数据作为训练集，使用 20%的数据作为交叉验证集，使用 20%的数据作为测试集

模型选择的方法为：

1. 使用训练集训练出 10 个模型
2. 用 10 个模型分别对交叉验证集计算得出交叉验证误差（代价函数的值）
3. 选取代价函数值最小的模型
4. 用步骤 3 中选出的模型对测试集计算得出推广误差（代价函数的值）
   3. 诊断偏差和方差
   
   
   过将训练集和交叉验证集的代价函数误差与多项式的次数绘制在同一张图表上来帮助分析：
   
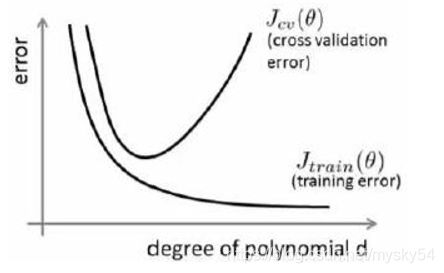
   解释：横坐标表示多项式的次数，纵坐标代表误差；
   对于训练集，当 较小时，模型拟合程度更低，误差较大；随着 的增长，拟合程度提高，误差减小。
   对于交叉验证集，当 较小时，模型拟合程度低，误差较大；但是随着 的增长，误差呈现先减小后增大的趋势，转折点是我们的模型开始过拟合训练数据集的时候。
   
   
   训练集误差和交叉验证集误差近似时：偏差/欠拟合
   交叉验证集误差远大于训练集误差时：方差/过拟合
   5.正则化和偏差/方差
   
   
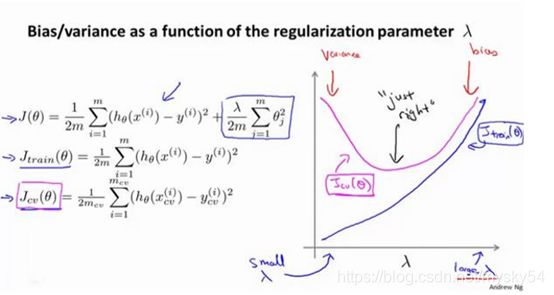
   当 较小时，训练集误差较小（过拟合）而交叉验证集误差较大，随着 的增加，训练集误差不断增加（欠拟合），而交叉验证集误差则是先减小后增加
   6. 学习曲线
   学习曲线是学习算法的一个很好的合理检验（sanity check）。学习曲线是将训练集误差和交叉验证集误差作为训练集实例数量（）的函数绘制的图表。
   
   在高偏差/欠拟合的情况下，增加数据到训练集不一定能有帮助。
   
   在高方差/过拟合的情况下，增加更多数据到训练集可能可以提高算法效果。
   
   总结：
   （1）获得更多的训练实例——解决高方差
   （2）尝试减少特征的数量——解决高方差
   （3）尝试获得更多的特征——解决高偏差
   （4）尝试增加多项式特征——解决高偏差
   （5）尝试减少正则化程度 λ——解决高偏差
   （6）尝试增加正则化程度 λ——解决高方差
   7. 类偏斜的误差度量
   查准率（Precision）和查全率（Recall）将算法预测的结果分成四种情况：
5. 正确肯定（True Positive,TP）：预测为真，实际为真
6. 正确否定（True Negative,TN）：预测为假，实际为假
7. 错误肯定（False Positive,FP）：预测为真，实际为假
8. 错误否定（False Negative,FN）：预测为假，实际为真
   查准率=TP/(TP+FP)。
   查全率=TP/(TP+FN)。
   
   二、编程作业
   1. linearRegCostFunction.m(Regularized linear regression
   cost function):implement regularized linear regression to predict the amount of water flowing out of a dam using the change of water level in a reservoir.
   regularized linear regression:
   
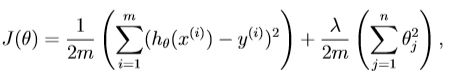
   the partial derivative of regularized linear regression’s cost for θj is defined as:
   

function [J, grad] = linearRegCostFunction(X, y, theta, lambda)           
% Initialize some useful values     
m = length(y); % number of training examples  
% You need to return the following variables correctly        
J = 0;       
grad = zeros(size(theta));        
J=1/(2*m)*(X*theta-y)'*(X*theta-y)+lambda/(2*m)*(theta'*theta-theta(1)^2);  
grad = 1/m*(X'*(X*theta-y));  
grad(2:end)=grad(2:end)+(lambda/m)*theta(2:end);    
grad = grad(:);  
end  

2.learningCurve.m(Generates a learning curve)：implement code to generate the learning curves that will be useful in
debugging learning algorithms.
training error for a dataset：

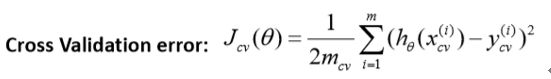
function [error_train, error_val] = ...      
    learningCurve(X, y, Xval, yval, lambda)             
% Number of training examples     
m = size(X, 1);             
% You need to return these values correctly      
error_train = zeros(m, 1);       
error_val   = zeros(m, 1);  
%模拟学习曲线，随着训练集m的增大，曲线逐渐靠近      
n = size(Xval,1); % number of cross validation set  
for i = 1:m     
    %计算theta值，找到拟合参数   
    theta = trainLinearReg(X(1:i,:), y(1:i,:), lambda);    
    %计算训练集的 cost    
    error_train(i) = 1/(2*i) * sum((X(1:i,:)*theta - y(1:i,:)).^2);        
     %计算交叉验证集的cost   
    error_val(i) = 1/(2*n) * sum((Xval*theta - yval).^2);    
end  

3. polyFeatures.m(Maps data into polynomial feature space)： address underfitting (high bias).by adding more features.
For use polynomial regression,our hypothesis has the form:

function [X_poly] = polyFeatures(X, p)           
% You need to return the following variables correctly.      
X_poly = zeros(numel(X), p);          
%X_poly(i, :) = [X(i) X(i).^2 X(i).^3 ...  X(i).^p];          
for i = 1 : p  
    X_poly(:,i) = X.^i;  
end;  
end  

4.validationCurve.m(Generates a cross validation curve)

function [lambda_vec, error_train, error_val] = ...  
    validationCurve(X, y, Xval, yval)          
% Selected values of lambda (you should not change this)      
lambda_vec = [0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10]';      
% You need to return these variables correctly.     
error_train = zeros(length(lambda_vec), 1);     
error_val = zeros(length(lambda_vec), 1);    
m = size(X, 1);  
n = size(Xval, 1);  
for i = 1 : length(lambda_vec)  
    lambda = lambda_vec(i);  
    theta = trainLinearReg(X,y,lambda);  
    error_train(i) = 1/(2*m) * sum((X*theta - y).^2);  % training error      
    error_val(i) = 1/(2*n) * sum((Xval*theta - yval).^2); % cross validation error     
end;  
end