计算机系统（四）：计算机网络中的安全（上篇）

目录

引言

5.1 什么是网络安全

5.2 密码学的原则

5.2.1 对称密钥密码体系

5.2.1.1 块密码

5.2.1.2 密码块链接

5.2.2 公开密钥加密

---

引言

在这一部分的学习中，我们将通篇使用 Alice 和 Bob 俩人的通信作为例子。他们俩是一种象征，可以代指两台需要安全交换路由选择表的路由器，也可以代指希望建立一个安全传输连接的客户端和服务器，或者是两个安全交换邮件的电子邮件应用程序。

Alice 和 Bob 希望他们之间的通信时安全的，比如，他们不希望信息被窃听者获取，他们要确保自己是在和对方通信，而不是一个伪装的第三者，或者是当通信内容被窃听者篡改后，Alice 和 Bob 都能检测到信息的破坏。接下来我们将更加具体的阐述这些问题。

5.1 什么是网络安全

我们指出，安全通信（secure communication）应该具有下列特征：

机密性（confidentiality）

仅有发送方和希望的接收方能够理解传输报文的内容。因为窃听者可以截获报文，这必须要求报文在一定程度上进行加密（encrypted），使截取的报文无法被截获者所理解。

报文完整性（message integrity）

Alice和Bob希望确保其通信的内容在传输过程中未被改变——或者恶意篡改或者意外改动。

端点鉴别（end-point authentication）

发送方和接收方都应该能证实通信过程所涉及的另一方，以确信通信的另一方确实具有他们所声称的身份。

运行安全性（operational security）

与公共因特网相连接的网络都潜在地能够被危及安全。攻击者能够试图在网络主机中安放蠕虫，获取机构秘密，勘察内部网络配置并发起DoS攻击。我们需要使用诸如防火墙和人侵检测系统等运行设备正被用于反制对机构网络的攻击。防火墙位于机构网络和公共网络之间，控制接人和来自网络的分组。人侵检测系统执行“深度分组检查”任务，向网络管理员发出有关可疑活动的警告。

明确了网络安全的具体含义后，我们再定义一下入侵者可能执行的行为：

窃听——监听并记录信道上传输的控制报文和数据报文。

修改、插入或删除报文或报文内容。

5.2 密码学的原则

我们通过这张图，来学习密码学中的一些重要术语：

明文（plaintext, cleartext）

Alice要向Bob发送一个报文。Alice报文的最初形式被称为明文。

加密算法（encryption algorithm）

Alice 使用加密算法加密其明文报文，

密文（eiphertext）

通过加密算法生成的加密报文被称为密文，该密文对任何人侵者看起来是不可懂的。

那是不是我们只需要加密算法就可以完成安全通信。但在许多现代密码系统中，包括因特网上所使用的那些加密算法，是公开发行的、标准化的和任何人都可使用的，即使对潜在的人侵者也是如此！所以我们需要使用一个秘密信息来阻止入侵者解密被传输的数据，即使用密钥。

密钥（key）

Alice提供了一个密钥，它是一串数字或字符，作为加密算法的输入。加密算法以密钥和明文报文m为输入，生成的密文作为输出。用符号表示使用密钥加密的明文报文m的密文形式。也就意味着使用密钥的实际加密算法与上下文有关。

解密算法（decryption algorithm） 

类似的，Bob将为解密算法提供密钥，将密文和Bob的密钥作为输入，输出初始明文。即，Bob接收到一个加密的报文，他可通过计算进行解密。

对称密钥系统（symmetric key system）

对称密钥系统中，Alice和Bob的密钥是相同的并且是秘密的。

公开密钥系统（public key system）

公开密钥系统中，使用一对密钥：一个密钥为所有人所知，另一个密钥只有Bob或Alice知道（而不是双方都知道）。

5.2.1 对称密钥密码体系

首先我们从一个古老简单的对称密钥算法开始，凯撒密码用于英语文本时，将明文报文中的每个字母用字母表中该字母后第k个字母进行替换（允许回绕，即把 a 排在 z 之后）。它加密简单，破译也简单，因为密钥值只有25个，只要你知道了凯撒密码的原理，不久就可以破译密文。

凯撒密码的一种改进方法是单码代替密码，就是使用字母表中的一个字母代替另一个字母，而不是按照一定规则替换。这种密码之所以优于凯撒密码是因为它的字母配对可能性是（10的26次方数量级）。

但是它也存在问题，因为不同字母的使用频率是不同的，还有一些常见的字母组合，如果入侵者大概知道密文的可能内容，那破译难度就会直线下降。上述所说的入侵者降低破译难度的方法是有术语解释的:

唯密文攻击

人侵者只得到截取的密文，也不了解明文报文的内容。入侵者可以在此情况下对数据进行统计分析。

已知明文攻击

入侵者知道（明文，密文）的部分匹配关系。

选择明文攻击

人侵者能够选择某一明文报文并得到该明文报文对应的密文形式。对于简单的加密算法，选择明文攻击可以导致现在的密文被破译，但对于复杂的加密算法，明文攻击不一定能攻破该加密机制。

对单码代替密码的改进是多码代替密码。它的思想就是使用多个单码代替密码。具体的实现方式是，一个单码代替密码用于加密某明文报文中一个特定位置的一个字母。因此，在某明文报文中不同位置出现的相同字母可能以不同的方式编码。

例如，我们使用两个凯撒密码（k = 5 和 19），如下图所示：

加密时采用以，，，，的次序进行循环，即第一个字母用加密，第二个和第三个字母使用加密，以此类推。对于这个例子，我们要想实现加密和解密，要知道和，以及加密时 和 循环的次序。

5.2.1.1 块密码

我们在上面介绍了一些古老的对称加密算法。现在我们需要学习对称加密技术今天的工作方式，对称加密技术有两种宽泛的类型：流密码（stream ciphers）和块密码（block ciphers）。我们在研究无线局域网的时候会使用到流密码，但是我们主要研究块密码。

在块密码中，要加密的报文被处理为k比特的块。例如，如果 k=64， 则报文被划分为64比特的块，每块被独立加密。为了加密一个块，该密码采用了一对一映射，将 h 比特块的明文映射为k比特块的密文。我们通过一个具体的例子学习：

假设 k=3，因此块密码将3比特输入（明文）映射为3比特输出（密文）。这是一个一对一的映射，即对每种输入有不同的输出。这种块密码将报文划分成3比特的块并根据映射关系进行加密。可以验证，报文010 110 001 111被加密成了101 000 111 001。

上述映射只是许多可能映射中的一种，有多少种可能的映射呢？每一种映射其实是3比特0和1的所有排列组合，共有种可能的输入，这8种输入能够排列为种不同方式。因为这些排列的每种都定义了一种映射，共有种可能的映射。每一种映射就是一个密钥。

但是对于现在计算机的算力，种可能映射的蛮力破解可以在一台PC上迅速完成，所以块密码会使用大的多的块，对于通常的k比特块密码，可能的映射数量为，所以我们一般取k = 64或者更大。

虽然全表块密码对于不大的k值能够产生健壮的对称密钥加密方案，但它们难以实现。当k = 64时，Alice要和Bob维护一张具有个输入值的表。并且每次改变密钥都要重新生成该表。因此，像全表块密码这样在所有输入和输出之间提供预先决定的完整映射关系是不太可能实现的事。

为了解决这个问题，块密码通常使用函数模拟随机排列表。我们举一个函数的例子，如下图所示：

当k=64时，该函数首先将64比特块划分为8个块，每个块由8比特组成。每个8比特块由一个“8比特到8比特”表处理，这个长度是可管理的。例如，第一个块由标志为的表来处理。接下来，这8个输出块被重新装配成一个64比特的块。该输出被回馈到64比特的输入，开始了第二次循环。经n次这样的循环后，该函数提供了一个64比特的密文块。 这种块密码算法的密钥是这8张排列表（假定置乱函数是公共已知的）。 

为什么要循环n次呢，这是因为如果仅使用一次循环，一个给定的输入比特将仅影响64输出比特中的8比特。而通过多次循环，多次将64比特划分为8比特，使得每个输入比特影响最后输出比特的大部分（并不一定是影响到全部比特）。

目前有一些流行的块密码，包括DES（Data Encryption Standard， 数据加密标准）、3DES和AES（Advanced Encryption Standard，高级加密标准）。这些标准中的每种都使用了函数（而不是预先决定的表），不同的算法它们在图中表示的连线也不同，具体到每种密码上来说会更为复杂。

这些算法中的每种也使用了比特串作为密钥。DES使用了具有56比特密钥的64比特块。AES使用128比特块，能够使用128、192 和256比特长的密钥进行操作。一个算法的密钥决定了特定“小型表”的映射和该算法内部的排列。

对这些密码中的每种进行蛮力攻击要循环通过所有密钥，用每个密钥应用解密算法。采用长度为n的密钥，有种可能的密钥。蛮力破解就要尝试种密钥。

5.2.1.2 AES的ECB模式

AES（Advanced Encryption Standard，高级加密标准），它的特点是：

• 对称密钥对称分组密码
• 128 位数据，128/192/256 位密钥
• 比 Triple-DES 更强更快
• 提供完整的规格和设计细节
• 可在 C 和 Java 中实现的软件

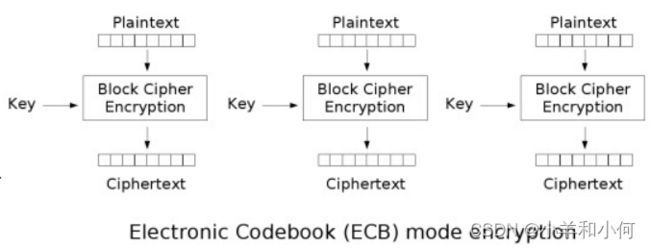
AES中一个常见的工作体制是ECB模式（Electric CodeBook Mode）。ECB模式的运作原理就是将明文所切成的明文区块直接当成加密演算法的输入，如图：

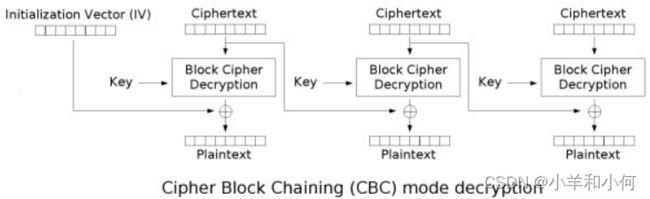
解密过程是：

使用ECB模式加密后，明文区块与密文区块是类似一对一的关系。这个问题我们已经在计算机网络中的安全（上篇）里探讨过了。入侵者可以利用这个信息猜出明文，并通过识别相同的密文块和利用支撑协议结构的知识，是能够解密整个报文的。我们可以通过一个直观的图看出来：

上面这两个对比图诠释了什么叫加密了但没完全加密，所以不建议使用ECB模式。对于ECB模式，我们的改进有上面所说的，将输出经过64比特置乱函数组合成新的64比特报文，然后再次当成输入，以此类推循环n次。还有一个改进是使用密码块链接。

5.2.1.3 密码块链接

使用上面的块密码对整个报文进行切合是存在问题的，因为报文中可能会出现重复的明文块，这就意味着产生相同的块密码，这是一个潜在的威胁，入侵者可以利用这个信息猜出明文，并通过识别相同的密文块和利用支撑协议结构的知识，是能够解密整个报文的。

所以我们需要能够加密长报文（或长数据流）。即在密文中混合某些随机性，使得相同的明文块也能产生不同的密文块。我们来进一步解释这个思路。

令表示第个密文块，具有密钥S的块密码的加密算法表示为，代表两个比特段的异或（XOR）:

	1	0	1	0
	1	0	0	1
	0	0	1	1

例如：

我们这样描述这个过程：

发送方为第块生成一个随机的比特数，并计算。注意，是为每块选择一个新的比特随机数。发送方发送等等。然后接收方拿到和，通过计算恢复每个明文块。尽管是明文发送的，入侵者窃取到了也因为不知道密钥 ，无法得到。

我们能注意到，引入随机性造成了发送者必需传输是以前两倍的比特，因为要发送，这使得带宽加倍。为了解决这个问题并不舍弃随机性的优点，块密码通常使用密码块链接（Cipher Block Chaining，CBC）技术。

CBC的基本思想是仅随第一个报文发送一个随机值，然后让发送方和接收方使用计算的编码块代替后继的随机数。我们具体描述一下这个过程：

• 在加密报文（或数据流）之前，发送方生成一个随机的比特串，称为初始向量（Initialization Vector，IV），将这个初始向量表示为，并以明文的方式将IV发送给接收方。
• 对于第一个块，发送方将和进行异或计算，然后再将其通过块密码算法变成密文块，这一步的总运算式为，然后将发送给接收方。
• 对于第个块，发送方根据生成第个密文块。

接收方在收到后可以利用解密得到；又因为接收方已经知道，他可以得到。

我们用两张图更直观的展示这一过程，首先是加密过程：

我们可以从上图看出，加密必须按顺序进行，但是解密可以并行进行，如下图所示：

当密文块或IV的丢失或损坏时，最多影响两个块的正确解密：

密码块链接的优点是：

即使两个明文块是相同的，它们的密文块几乎总是不同的。

虽然最初的IV是明文发送的，但因为入侵者不知道密钥S，他依然无法解密密文块。

密码块链接只增加了细微的带宽，因为它只需要在最开始额外发一个IV。

5.2.2 公开密钥加密

对称密钥加密存在的问题是，通信双方在互通密钥时要保证通信安全。可是还没有共享密钥的他们该如何加密通信呢...。为了解决这个问题，公开密钥加密提供了一个全新优雅的方案。

我们结合这张图解释一下公开密钥加密的使用。Bob拥有两个密钥，一个是所有人都知道的公钥（public key），另一个是只有Bob自己知道的私钥（private key）。Alice首先取得Bob的公钥，然后用这个和一个众所周知的加密算法，加密她要传递给Bob的报文m，即运算。Bob在收到Alice的密文后，用他的私钥和一个众所周知的解密算法解密密文，即运算。通过这种方式，他们任一方都无须分发任何密钥！公钥和私钥加密相互交换同样能够得到m，即。

但是公开密钥加密就没有问题了吗，当然不是，首先，因为入侵者也知道Bob的公钥，他就可以截取Alice发送的密文，又因为Alice使用的加密算法是公开的，入侵者就可以发起选择明文攻击。其次，入侵者可以利用公钥伪装成Alice加密一段明文，然后发送给Bob，这也是我们后面要用到数字签名的原因。

以上就是我们上半部分内容，主要讲述了如何使用密码术为两个通信实体提供机密性，在下篇的内容中我们将探讨报文完整性和数字签名这两个重要方面。