统计学习方法笔记(未完待续)

前言：
参考了一位NLP学长的博客，受益颇多，跟着学长学习李航老师的《统计学习方法》，希望整理一些重点，便于翻阅，日积月累，为三年后的面试打下基础！
代码来自：
https://www.pkudodo.com

（一）感知机

定义：

感知机是二分类的线性模型,属于判别模型.感知机学习旨在求出将训练数据进行线性划分的分离超平面.是神经网络和支持向量机的基础。

个人理解：结合看过的《深度学习入门基于python的理论与实现》，感知机说白了就是接受一些信号，输出信号的模型（就像理工科电工科中讲到的逻辑电路一个道理），多个输入信号都有各自固有的权重，这些权重发挥着控制各个信号的重要性的作用，也就是说，权重越大，对应该权重的信号的重要性就越高。


那么，有同学就疑问了，为什么是线性呢，非线性不能吗，这里可以看看两张图：

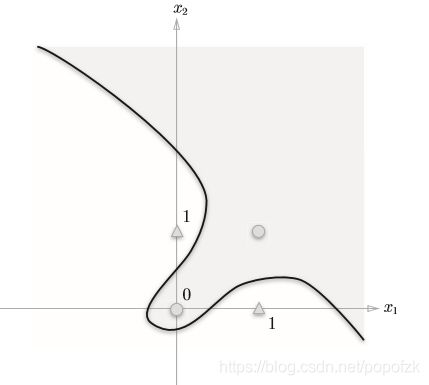
用一条直线是可以将图1正常分割开，而无法将第二张图分割，第一张图在编程实现时用到的是简单的逻辑电路（与门、与非门、或门），但是第二张图这种异或门只能通过多层感知机，也就是神经网络才能够实现。

感知机的几何解释:
模型公式:$f(x)=sign(w\cdot x+b)$
$w$叫作权值向量,$b$叫做偏置,$sign$是符号函数.
$w\cdot x+b$对应于特征空间中的一个分离超平面$S$,其中$w$是$S$的法向量,$b$是$S$的截距.$S$将特征空间划分为两个部分,位于两个部分的点分别被分为正负两类.

策略:
假设训练数据集是线性可分的,感知机的损失函数是误分类点到超平面$S$的总距离。因为误分类点到超平面S的距离是$\frac{1}{||w||}|w\cdot x_0+b|$.且对于误分类的数据来说,总有:$-y_i(w\cdot x_i+b)>0$成立,因此不考虑$\frac{1}{||w||}$,就得到感知机的损失函数:
$L(w,b)=-{\sum }_{x_i\in M}{y}_i(w\cdot x_i+b)$,其中$M$是误分类点的集合.感知机学习的策略就是选取使损失函数最小的模型参数.

算法:感知机的最优化方法采用随机梯度下降法.首先任意选取一个超平面$w0$,$b0$,然后不断地极小化目标函数.在极小化过程中一次随机选取一个误分类点更新$w,b$,直到损失函数为0:
$$w⟵w+\eta y_i{x}_i$$
$$b⟵b+\eta y_i$$
其中$\eta$表示步长.该算法的直观解释是:当一个点被误分类,就调整$w,b$使分离超平面向该误分类点接近.感知机的解可以不同.

对偶形式: 假设原始形式中的$w_0$和$b_0$均为0,设逐步修改$w$和$b$共$n$次,令$a=n\eta$,最后学习到的$w,b$可以表示为$w={\sum }_{i=1}^N\alpha y_i{x}_i,$.那么对偶算法就变为设初始a和b均为0,每次选取数据更新a和b直至没有误分类点为止.对偶形式的意义在于可以将训练集中实例间的内积计算出来,存在Gram矩阵中,可以大大加快训练速度

代码：

参考代码:

#coding=utf-8
#Author:Dodo
#Date:2018-11-15
#Email:[email protected]
'''
数据集：Mnist
训练集数量：60000
测试集数量：10000
------------------------------
运行结果：
正确率：81.72%（二分类）
运行时长：78.6s
'''
import numpy as np
import time
def loadData(fileName):
    '''
    加载Mnist数据集
    :param fileName:要加载的数据集路径
    :return: list形式的数据集及标记
    '''
    print('start to read data')
    # 存放数据及标记的list
    dataArr = []; labelArr = []
    # 打开文件
    fr = open(fileName, 'r')
    # 将文件按行读取
    for line in fr.readlines():
        # 对每一行数据按切割福','进行切割，返回字段列表
        curLine = line.strip().split(',')
        # Mnsit有0-9是个标记，由于是二分类任务，所以将>=5的作为1，<5为-1
        if int(curLine[0]) >= 5:
            labelArr.append(1)
        else:
            labelArr.append(-1)
        #存放标记
        #[int(num) for num in curLine[1:]] -> 遍历每一行中除了以第一哥元素（标记）外将所有元素转换成int类型
        #[int(num)/255 for num in curLine[1:]] -> 将所有数据除255归一化(非必须步骤，可以不归一化)
        dataArr.append([int(num)/255 for num in curLine[1:]])
    #返回data和label
    return dataArr, labelArr
def perceptron(dataArr, labelArr, iter=50):
    '''
    感知器训练过程
    :param dataArr:训练集的数据 (list)
    :param labelArr: 训练集的标签(list)
    :param iter: 迭代次数，默认50
    :return: 训练好的w和b
    '''
    print('start to trans')
    #将数据转换成矩阵形式（在机器学习中因为通常都是向量的运算，转换成矩阵形式方便运算）
    #转换后的数据中每一个样本的向量都是横向的
    dataMat = np.mat(dataArr)
    #将标签转换成矩阵，之后转置(.T为转置)。
    #转置是因为在运算中需要单独取label中的某一个元素，如果是1xN的矩阵的话，无法用label[i]的方式读取
    #对于只有1xN的label可以不转换成矩阵，直接label[i]即可，这里转换是为了格式上的统一
    labelMat = np.mat(labelArr).T
    #获取数据矩阵的大小，为m*n
    m, n = np.shape(dataMat)
    #创建初始权重w，初始值全为0。
    #np.shape(dataMat)的返回值为m，n -> np.shape(dataMat)[1])的值即为n，与
    #样本长度保持一致
    w = np.zeros((1, np.shape(dataMat)[1]))# 初始化权重w为1*N的0矩阵
    #初始化偏置b为0
    b = 0
    #初始化步长，也就是梯度下降过程中的n，控制梯度下降速率
    h = 0.0001

    #进行iter次迭代计算
    for k in range(iter):
        #对于每一个样本进行梯度下降
        #李航书中在2.3.1开头部分使用的梯度下降，是全部样本都算一遍以后，统一
        #进行一次梯度下降
        #在2.3.1的后半部分可以看到（例如公式2.6 2.7），求和符号没有了，此时用
        #的是随机梯度下降，即计算一个样本就针对该样本进行一次梯度下降。
        #两者的差异各有千秋，但较为常用的是随机梯度下降。
        for i in range(m):
            #获取当前样本的向量
            xi = dataMat[i]
            #获取当前样本所对应的标签
            yi = labelMat[i]
            #判断是否是误分类样本
            #误分类样本特征为： -yi(w*xi+b)>=0，详细可参考书中2.2.2小节
            #在书的公式中写的是>0，实际上如果=0，说明改点在超平面上，也是不正确的
            if -1 * yi * (w * xi.T + b) >= 0:
                #对于误分类样本，进行梯度下降，更新w和b
                w = w + h *  yi * xi
                b = b + h * yi
        #打印训练进度
        print('Round %d:%d training' % (k, iter))

    #返回训练完的w、b
    return w, b
def test(dataArr, labelArr, w, b):
    '''
    测试准确率
    :param dataArr:测试集
    :param labelArr: 测试集标签
    :param w: 训练获得的权重w
    :param b: 训练获得的偏置b
    :return: 正确率
    '''
    print('start to test')
    #将数据集转换为矩阵形式方便运算
    dataMat = np.mat(dataArr)
    #将label转换为矩阵并转置，详细信息参考上文perceptron中
    #对于这部分的解说
    labelMat = np.mat(labelArr).T

    #获取测试数据集矩阵的大小
    m, n = np.shape(dataMat)
    #错误样本数计数
    errorCnt = 0
    #遍历所有测试样本
    for i in range(m):
        #获得单个样本向量
        xi = dataMat[i]
        #获得该样本标记
        yi = labelMat[i]
        #获得运算结果
        result = -1 * yi * (w * xi.T + b)
        #如果-yi(w*xi+b)>=0，说明该样本被误分类，错误样本数加一
        if result >= 0: errorCnt += 1
    #正确率 = 1 - （样本分类错误数 / 样本总数）
    accruRate = 1 - (errorCnt / m)
    #返回正确率
    return accruRate
if __name__ == '__main__':
    #获取当前时间
    #在文末同样获取当前时间，两时间差即为程序运行时间
    start = time.time()

    #获取训练集及标签
    trainData, trainLabel = loadData('./mnist_train.csv')
    #获取测试集及标签
    testData, testLabel = loadData('./mnist_test.csv')

    #训练获得权重
    w, b = perceptron(trainData, trainLabel, iter = 30)
    #进行测试，获得正确率
    accruRate = test(testData, testLabel, w, b)

    #获取当前时间，作为结束时间
    end = time.time()
    #显示正确率
    print('accuracy rate is:', accruRate)
    #显示用时时长
    print('time span:', end - start)

（二）K-邻近

定义：

$k$近邻法根据其$k$个最邻的训练实例的类别,通过多数表决等方式进行预测.

什么是多数表决？我们为了对样本$x$进行归类，通过它周围最近的$k$个点来“投票”，这$k$个点大多数是哪个类型的，则定样本$x$为这个类型，故称为多数表决

模型说明:
(1)训练集（样本$x$以及样本$x$对应的label:$y$）
(2)距离度量(欧氏距离or曼哈顿距离) 特征空间中两个实例点的距离是相似程度的反映,k近邻算法一般使用欧氏距离,也可以使用曼哈顿距离.
欧式距离：
曼哈顿距离：
(3)k值 k值较小时,整体模型变得复杂,容易发生过拟合;k值较大时,整体模型变得简单.在应用中k一般取较小的值,通过交叉验证法选取最优的k.

但是K邻近算法也有其局限性：

1. 在预测样本类别时，待预测样本需要与训练集中所有样本计算距离，当训练集数量过高时（例如Mnsit训练集有60000个样本），每预测一个样本都要计算60000个距离，计算代价过高，尤其当测试集数目也较大时（Mnist测试集有10000个）。

2. K近邻在高维情况下时（高维在机器学习中并不少见），待预测样本需要与依次与所有样本求距离。向量维度过高时使得欧式距离的计算变得不太迅速了。本文在60000训练集的情况下，将10000个测试集缩减为200个，整个过程仍然需要308秒（曼哈顿距离为246秒，但准确度大幅下降）。

3. 使用欧氏距离还是曼哈顿距离，性能上的差别相对来说不是很大，说明欧式距离并不是制约计算速度的主要方式。最主要的是训练集的大小，每次预测都需要与60000个样本进行比对，同时选出距离最近的$k$项
   
   

代码：

参考代码:

#coding=utf-8
#Author:Dodo
#Date:2018-11-16
#Email:[email protected]

'''
数据集：Mnist
训练集数量：60000
测试集数量：10000（实际使用：200）
------------------------------
运行结果：（邻近k数量：25）
向量距离使用算法——欧式距离
    正确率：97%
    运行时长：308s
向量距离使用算法——曼哈顿距离
    正确率：14%
    运行时长：246s
'''

import numpy as np
import time

def loadData(fileName):
    '''
    加载文件
    :param fileName:要加载的文件路径
    :return: 数据集和标签集
    '''
    print('start read file')
    #存放数据及标记
    dataArr = []; labelArr = []
    #读取文件
    fr = open(fileName)
    #遍历文件中的每一行
    for line in fr.readlines():
        #获取当前行，并按“，”切割成字段放入列表中
        #strip：去掉每行字符串首尾指定的字符（默认空格或换行符）
        #split：按照指定的字符将字符串切割成每个字段，返回列表形式
        curLine = line.strip().split(',')
        #将每行中除标记外的数据放入数据集中（curLine[0]为标记信息）
        #在放入的同时将原先字符串形式的数据转换为整型
        dataArr.append([int(num) for num in curLine[1:]])
        #将标记信息放入标记集中
        #放入的同时将标记转换为整型
        labelArr.append(int(curLine[0]))
    #返回数据集和标记
    return dataArr, labelArr

def calcDist(x1, x2):
    '''
    计算两个样本点向量之间的距离
    使用的是欧氏距离，即 样本点每个元素相减的平方  再求和  再开方
    欧式举例公式这里不方便写，可以百度或谷歌欧式距离（也称欧几里得距离）
    :param x1:向量1
    :param x2:向量2
    :return:向量之间的欧式距离
    '''
    return np.sqrt(np.sum(np.square(x1 - x2)))

    #马哈顿距离计算公式
    # return np.sum(x1 - x2)




def getClosest(trainDataMat, trainLabelMat, x, topK):
    '''
    预测样本x的标记。
    获取方式通过找到与样本x最近的topK个点，并查看它们的标签。
    查找里面占某类标签最多的那类标签
    （书中3.1 3.2节）
    :param trainDataMat:训练集数据集
    :param trainLabelMat:训练集标签集
    :param x:要预测的样本x
    :param topK:选择参考最邻近样本的数目（样本数目的选择关系到正确率，详看3.2.3 K值的选择）
    :return:预测的标记
    '''
    #建立一个存放向量x与每个训练集中样本距离的列表
    #列表的长度为训练集的长度，distList[i]表示x与训练集中第
    ## i个样本的距离
    distList = [0] * len(trainLabelMat)
    #遍历训练集中所有的样本点，计算与x的距离
    for i in range(len(trainDataMat)):
        #获取训练集中当前样本的向量
        x1 = trainDataMat[i]
        #计算向量x与训练集样本x的距离
        curDist = calcDist(x1, x)
        #将距离放入对应的列表位置中
        distList[i] = curDist

    #对距离列表进行排序
    #argsort：函数将数组的值从小到大排序后，并按照其相对应的索引值输出
    #例如：
    #   >>> x = np.array([3, 1, 2])
    #   >>> np.argsort(x)
    #   array([1, 2, 0])
    #返回的是列表中从小到大的元素索引值，对于我们这种需要查找最小距离的情况来说很合适
    #array返回的是整个索引值列表，我们通过[:topK]取列表中前topL个放入list中。
    #----------------优化点-------------------
    #由于我们只取topK小的元素索引值，所以其实不需要对整个列表进行排序，而argsort是对整个
    #列表进行排序的，存在时间上的浪费。字典有现成的方法可以只排序top大或top小，可以自行查阅
    #对代码进行稍稍修改即可
    #这里没有对其进行优化主要原因是KNN的时间耗费大头在计算向量与向量之间的距离上，由于向量高维
    #所以计算时间需要很长，所以如果要提升时间，在这里优化的意义不大。（当然不是说就可以不优化了，
    #主要是我太懒了）
    topKList = np.argsort(np.array(distList))[:topK]        #升序排序
    #建立一个长度时的列表，用于选择数量最多的标记
    #3.2.4提到了分类决策使用的是投票表决，topK个标记每人有一票，在数组中每个标记代表的位置中投入
    #自己对应的地方，随后进行唱票选择最高票的标记
    labelList = [0] * 10
    #对topK个索引进行遍历
    for index in topKList:
        #trainLabelMat[index]：在训练集标签中寻找topK元素索引对应的标记
        #int(trainLabelMat[index])：将标记转换为int（实际上已经是int了，但是不int的话，报错）
        #labelList[int(trainLabelMat[index])]：找到标记在labelList中对应的位置
        #最后加1，表示投了一票
        labelList[int(trainLabelMat[index])] += 1
    #max(labelList)：找到选票箱中票数最多的票数值
    #labelList.index(max(labelList))：再根据最大值在列表中找到该值对应的索引，等同于预测的标记
    return labelList.index(max(labelList))


def test(trainDataArr, trainLabelArr, testDataArr, testLabelArr, topK):
    '''
    测试正确率
    :param trainDataArr:训练集数据集
    :param trainLabelArr: 训练集标记
    :param testDataArr: 测试集数据集
    :param testLabelArr: 测试集标记
    :param topK: 选择多少个邻近点参考
    :return: 正确率
    '''
    print('start test')
    #将所有列表转换为矩阵形式，方便运算
    trainDataMat = np.mat(trainDataArr); trainLabelMat = np.mat(trainLabelArr).T
    testDataMat = np.mat(testDataArr); testLabelMat = np.mat(testLabelArr).T

    #错误值技术
    errorCnt = 0
    #遍历测试集，对每个测试集样本进行测试
    #由于计算向量与向量之间的时间耗费太大，测试集有6000个样本，所以这里人为改成了
    #测试200个样本点，如果要全跑，将行注释取消，再下一行for注释即可，同时下面的print
    #和return也要相应的更换注释行
    # for i in range(len(testDataMat)):
    for i in range(200):
        # print('test %d:%d'%(i, len(trainDataArr)))
        print('test %d:%d' % (i, 200))
        #读取测试集当前测试样本的向量
        x = testDataMat[i]
        #获取预测的标记
        y = getClosest(trainDataMat, trainLabelMat, x, topK)
        #如果预测标记与实际标记不符，错误值计数加1
        if y != testLabelMat[i]: errorCnt += 1

    #返回正确率
    # return 1 - (errorCnt / len(testDataMat))
    return 1 - (errorCnt / 200)



if __name__ == "__main__":
    start = time.time()

    #获取训练集
    trainDataArr, trainLabelArr = loadData('./mnist_train.csv')
    #获取测试集
    testDataArr, testLabelArr = loadData('./mnist_test.csv')
    #计算测试集正确率
    accur = test(trainDataArr, trainLabelArr, testDataArr, testLabelArr, 25)
    #打印正确率
    print('accur is:%d'%(accur * 100), '%')

    end = time.time()
    #显示花费时间
print('time span:', end - start)

（三）朴素贝叶斯

定义 ：

朴素贝叶斯是基于贝叶斯定理和特征条件独立假设的分类方法。
首先学习输入/输出的联合概率分布,然后基于此模型,对给定的输入$x$,利用贝叶斯定理求出后验概率最大的输出$y$。

模型:
首先学习先验概率分布：$P(Y=c_k),k=1,2,...,K$ , $c_k$代表某一类，也就是计算该类别的概率（在样本中我们已知）
然后学习条件概率分布：$P(X=x|Y=c_k)=P(X^1=x^1,...,X^n=x^n|Y=c_k)$，给定一个类别$c_k$，计算该样本各个特征的概率,比如该样本第一个特征为
朴素贝叶斯法对条件概率分布作了条件独立性的假设：$$P(X^{(1)}=x^{(1)}|Y=c_k)P(X^{(2)}=x^{(2)}|Y=c_k)...P(X^{(j)}=x^{(j)}|Y=c_k)$$
上式变成:$$\prod _{j=1}^{n}P(X^{(j)}=x^{(j)}|Y=c_k)$$
在分类时,通过学习到的模型计算后验概率分布,由贝叶斯定理得到:
$$P(Y=c_k|X=x)=\frac{P(X=x|Y=c_k)P(Y=c_k)}{{\sum }_{k}P(X=x|Y=c_k)P(Y=c_k)}$$
将条件独立性假设得到的等式代入,并且注意到分母都是相同的,所以得到朴素贝叶斯分类器:
$$y=argma{x}_{c_k}P(Y=c_k)\prod _{j=1}P(X^{(j)}=x^{(j)}|Y=c_k)$$

算法:使用极大似然估计法估计相应的先验概率率:$$P(Y=c_k)=\frac{{\sum }_{i=1}^{N}I(y_i=c_k)}{N},k=1,2,...,K$$
以及条件概率：
$$P(X^{(j)}=a_{jl}|Y=c_k)=\frac{{\sum }_{i=1}^{N}I(x_i^{(j)}=a_{jl},y_i=c_k)}{{\sum }_{i=1}^{N}I(y_i=c_k)}$$
计算条件独立性假设下的实例各个取值的可能性,选取其中的最大值作为输出。

使用贝叶斯估计虽然保证了所有连乘项的概率都大于0，不会再出现某一项为0结果为0的情况。但若一个样本数据时高维的，比如说100维（100其实并不高），连乘项都是0-1之间的，那100个0-1之间的数相乘，最后的数一定是非常非常小了，可能无限接近于0。对于程序而言过于接近0的数可能会造成下溢出，也就是精度不够表达了。所以我们会给整个连乘项取对数，这样哪怕所有连乘最后结果无限接近0，那取完log以后数也会变得很大（虽然是负的很大），计算机就可以表示了。同样，多项连乘取对数，对数的连乘可以表示成对数的相加，在计算上也简便了。所以在实际运用中，不光需要使用贝叶斯估计（保证概率不为0），同时也要取对数（保证连乘结果不下溢出）。

代码：

参考代码:

# coding=utf-8
# Author:Dodo
# Date:2018-11-17
# Email:[email protected]

'''
数据集：Mnist
训练集数量：60000
测试集数量：10000
------------------------------
运行结果：
    正确率：84.3%
    运行时长：103s
'''

import numpy as np
import time

def loadData(fileName):
    '''
    加载文件
    :param fileName:要加载的文件路径
    :return: 数据集和标签集
    '''
    #存放数据及标记
    dataArr = []; labelArr = []
    #读取文件
    fr = open(fileName)
    #遍历文件中的每一行
    for line in fr.readlines():
        #获取当前行，并按“，”切割成字段放入列表中
        #strip：去掉每行字符串首尾指定的字符（默认空格或换行符）
        #split：按照指定的字符将字符串切割成每个字段，返回列表形式
        curLine = line.strip().split(',')
        #将每行中除标记外的数据放入数据集中（curLine[0]为标记信息）
        #在放入的同时将原先字符串形式的数据转换为整型
        #此外将数据进行了二值化处理，大于128的转换成1，小于的转换成0，方便后续计算
        dataArr.append([int(int(num) > 128) for num in curLine[1:]])
        #将标记信息放入标记集中
        #放入的同时将标记转换为整型
        labelArr.append(int(curLine[0]))
    #返回数据集和标记
    return dataArr, labelArr

def NaiveBayes(Py, Px_y, x):
    '''
    通过朴素贝叶斯进行概率估计
    :param Py: 先验概率分布
    :param Px_y: 条件概率分布
    :param x: 要估计的样本x
    :return: 返回所有label的估计概率
    '''
    #设置特征数目
    featrueNum = 784
    #设置类别数目
    classNum = 10
    #建立存放所有标记的估计概率数组
    P = [0] * classNum
    #对于每一个类别，单独估计其概率
    for i in range(classNum):
        #初始化sum为0，sum为求和项。
        #在训练过程中对概率进行了log处理，所以这里原先应当是连乘所有概率，最后比较哪个概率最大
        #但是当使用log处理时，连乘变成了累加，所以使用sum
        sum = 0
        #获取每一个条件概率值，进行累加
        for j in range(featrueNum):
            sum += Px_y[i][j][x[j]]
        #最后再和先验概率相加（也就是式4.7中的先验概率乘以后头那些东西，乘法因为log全变成了加法）
        P[i] = sum + Py[i]

    #max(P)：找到概率最大值
    #P.index(max(P))：找到该概率最大值对应的所有（索引值和标签值相等）
    return P.index(max(P))


def test(Py, Px_y, testDataArr, testLabelArr):
    '''
    对测试集进行测试
    :param Py: 先验概率分布
    :param Px_y: 条件概率分布
    :param testDataArr: 测试集数据
    :param testLabelArr: 测试集标记
    :return: 准确率
    '''
    #错误值计数
    errorCnt = 0
    #循环遍历测试集中的每一个样本
    for i in range(len(testDataArr)):
        #获取预测值
        presict = NaiveBayes(Py, Px_y, testDataArr[i])
        #与答案进行比较
        if presict != testLabelArr[i]:
            #若错误  错误值计数加1
            errorCnt += 1
    #返回准确率
    return 1 - (errorCnt / len(testDataArr))


def getAllProbability(trainDataArr, trainLabelArr):
    '''
    通过训练集计算先验概率分布和条件概率分布
    :param trainDataArr: 训练数据集
    :param trainLabelArr: 训练标记集
    :return: 先验概率分布和条件概率分布
    '''
    #设置样本特诊数目，数据集中手写图片为28*28，转换为向量是784维。
    # （我们的数据集已经从图像转换成784维的形式了，CSV格式内就是）
    featureNum = 784
    #设置类别数目，0-9共十个类别
    classNum = 10

    #初始化先验概率分布存放数组，后续计算得到的P(Y = 0)放在Py[0]中，以此类推
    #数据长度为10行1列
    Py = np.zeros((classNum, 1))
    #对每个类别进行一次循环，分别计算它们的先验概率分布
    #计算公式为书中"4.2节 朴素贝叶斯法的参数估计 公式4.8"
    for i in range(classNum):
        #下方式子拆开分析
        #np.mat(trainLabelArr) == i：将标签转换为矩阵形式，里面的每一位与i比较，若相等，该位变为Ture，反之False
        #np.sum(np.mat(trainLabelArr) == i):计算上一步得到的矩阵中Ture的个数，进行求和(直观上就是找所有label中有多少个
        #为i的标记，求得4.8式P（Y = Ck）中的分子)
        #np.sum(np.mat(trainLabelArr) == i)) + 1：参考“4.2.3节 贝叶斯估计”，例如若数据集总不存在y=1的标记，也就是说
        #手写数据集中没有1这张图，那么如果不加1，由于没有y=1，所以分子就会变成0，那么在最后求后验概率时这一项就变成了0，再
        #和条件概率乘，结果同样为0，不允许存在这种情况，所以分子加1，分母加上K（K为标签可取的值数量，这里有10个数，取值为10）
        #参考公式4.11
        #(len(trainLabelArr) + 10)：标签集的总长度+10.
        #((np.sum(np.mat(trainLabelArr) == i)) + 1) / (len(trainLabelArr) + 10)：最后求得的先验概率
        Py[i] = ((np.sum(np.mat(trainLabelArr) == i)) + 1) / (len(trainLabelArr) + 10)
    #转换为log对数形式
    #log书中没有写到，但是实际中需要考虑到，原因是这样：
    #最后求后验概率估计的时候，形式是各项的相乘（“4.1 朴素贝叶斯法的学习” 式4.7），这里存在两个问题：1.某一项为0时，结果为0.
    #这个问题通过分子和分母加上一个相应的数可以排除，前面已经做好了处理。2.如果特诊特别多（例如在这里，需要连乘的项目有784个特征
    #加一个先验概率分布一共795项相乘，所有数都是0-1之间，结果一定是一个很小的接近0的数。）理论上可以通过结果的大小值判断， 但在
    #程序运行中很可能会向下溢出无法比较，因为值太小了。所以人为把值进行log处理。log在定义域内是一个递增函数，也就是说log（x）中，
    #x越大，log也就越大，单调性和原数据保持一致。所以加上log对结果没有影响。此外连乘项通过log以后，可以变成各项累加，简化了计算。
    #在似然函数中通常会使用log的方式进行处理
    Py = np.log(Py)

    #计算条件概率 Px_y=P（X=x|Y = y）
    #计算条件概率分成了两个步骤，下方第一个大for循环用于累加，参考书中“4.2.3 贝叶斯估计 式4.10”，下方第一个大for循环内部是
    #用于计算式4.10的分子，至于分子的+1以及分母的计算在下方第二个大For内
    #初始化为全0矩阵，用于存放所有情况下的条件概率
    Px_y = np.zeros((classNum, featureNum, 2))
    #对标记集进行遍历
    for i in range(len(trainLabelArr)):
        #获取当前循环所使用的标记
        label = trainLabelArr[i]
        #获取当前要处理的样本
        x = trainDataArr[i]
        #对该样本的每一维特诊进行遍历
        for j in range(featureNum):
            #在矩阵中对应位置加1
            #这里还没有计算条件概率，先把所有数累加，全加完以后，在后续步骤中再求对应的条件概率
            Px_y[label][j][x[j]] += 1


    #第二个大for，计算式4.10的分母，以及分子和分母之间的除法
    #循环每一个标记（共10个）
    for label in range(classNum):
        #循环每一个标记对应的每一个特征
        for j in range(featureNum):
            #获取y=label，第j个特诊为0的个数
            Px_y0 = Px_y[label][j][0]
            #获取y=label，第j个特诊为1的个数
            Px_y1 = Px_y[label][j][1]
            #对式4.10的分子和分母进行相除，再除之前依据贝叶斯估计，分母需要加上2（为每个特征可取值个数）
            #分别计算对于y= label，x第j个特征为0和1的条件概率分布
            Px_y[label][j][0] = np.log((Px_y0 + 1) / (Px_y0 + Px_y1 + 2))
            Px_y[label][j][1] = np.log((Px_y1 + 1) / (Px_y0 + Px_y1 + 2))

    #返回先验概率分布和条件概率分布
    return Py, Px_y


if __name__ == "__main__":
    start = time.time()
    # 获取训练集
    print('start read transSet')
    trainDataArr, trainLabelArr = loadData('../Mnist/mnist_train.csv')

    # 获取测试集
    print('start read testSet')
    testDataArr, testLabelArr = loadData('../Mnist/mnist_test.csv')

    #开始训练，学习先验概率分布和条件概率分布
    print('start to train')
    Py, Px_y = getAllProbability(trainDataArr, trainLabelArr)

    #使用习得的先验概率分布和条件概率分布对测试集进行测试
    print('start to test')
    accuracy = test(Py, Px_y, testDataArr, testLabelArr)

    #打印准确率
    print('the accuracy is:', accuracy)
    #打印时间
    print('time span:', time.time() -start)

（四）决策树

定义：

书中实例：贷款申请样本，通过一个人的年龄、是否有工作、是否有自己的房子、信贷情况这四个特征判定，最终构建模型来判别是否给予贷款，如图：

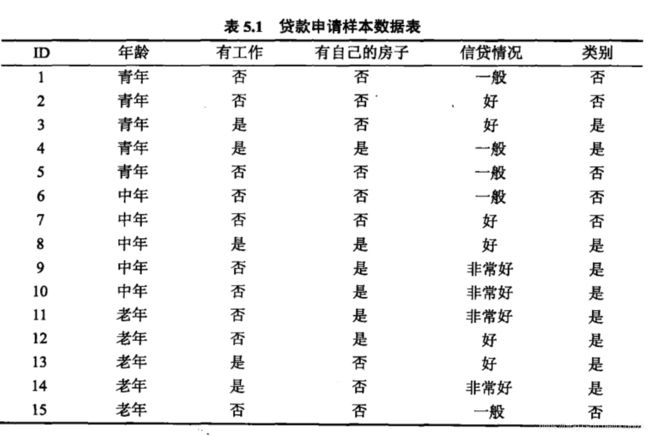
希望通过所给的训练数据学习一个贷款申请的决策树，用来对未来贷款申请进行分类（二分类），决策树可以理解成：有一个根节点开始，往下进行分支，越重要的节点应该离根越近，我们将重要的、影响度大的特征作为根节点，依次向下，其次重要的往下面街接，如图：

熵与条件熵的定义：
熵: 表示随机变量不确定性的度量，设$X$是一个取有限个值的离散随机变量，其概率分布为：$$P(X=x_i)=p_i,i=1,2,...,n$$
则随机变量$X$的熵定义为：
$$H(X)=-\sum _{i=1}^n{p}_i\log p_i$$
越大的概率，得到的熵值越小，也就是说概率大的确定性大，不确定不就小了嘛，反之亦然；
举例：$A$集合：[1,1,1,1,1,1,1,2,2]
           $B$集合：[1,2,3,4,5,6,7,8,9]
显然$A$集合的熵值要低，因为A里面只有两种类别，相对稳定一些，而B中类别太多，熵值就会大很多，而在分类问题中我们当然是希望分支后的数据类别的熵值小，确定性就大嘛，熵值越低，分类效果越好撒
同理条件熵 就是表示在已知随机变量X的条件下随机变量Y的不确定性$H(Y|X)$,定义为$X$给定条件下Y的条件概率分布的熵对X的数学期望：
$$H(Y|X)=\sum _{i=1}^n{p}_{i}H(Y|X=x_i)$$

信息增益：
做决策树目的就是在过程中将熵值不断减小，增益呢，就是熵值下降了多少，通过信息增益来遍历计算所有特征，哪个特征使得我们的信息增益最大，最大的哪个特征就拿过来当做根节点，接着同理把剩下的特征也这么来排序，排出第二个节点，第三个节点。。。
信息增益表示得知特征$X$的信息而使得类$Y$的信息不确定性减少的程度。
特征$A$对训练数据集$D$的信息增益$g(D,A)$,定义为集合$D$的经验熵，经验熵就是不考虑特征，只考虑整个样本label的熵，附上书中实例：

$H(D)$与特征$A$给定条件下$D$的经验条件熵$H(D|A)$之差，即：
$$g(D,A)=H(D)-H(D|A)$$
熵$H(Y)$与条件熵$H(Y|X)$之差成为互信息，此时信息增益等于互信息。
信息增益算法：
输入：训练数据集$D$和特征$A$；
输出：特征$A$对训练数据集$D$的信息增益$g(D,A)$。
(1)计算数据集$D$的经验熵$H(D)$
$$H(D)=-\sum _{k=1}^k\frac{|C_k|}{|D|}\log \frac{|C_k|}{|D|}$$
(2)计算特征$A$对数据集$D$的经验条件熵$H(D|A)$
$$H(D|A)=\sum _{i=1}^n\frac{|D_I|}{|D|}H(D_i)=-\sum _{i=1}^n\frac{|D_i|}{D}\sum _{k=1}^k\frac{|D_{ik}|}{D_i}{\log }_2\frac{|D_{ik}|}{|D_i|}$$
(3)计算信息增益：
$$g(D,A)=H(D)-H(D,A)$$

信息增益比：
以信息增益作为划分训练集的特征，存在偏向于选择取值较多的特征的问题，使用信息增益比对其校正：特征$A$对训练数据集$D$的信息增益比$g_R(D,A)$定义为其信息增益$g(D,A$与训练数据集$D$关于特征$A$的值的熵$H_A(D)$之比，即：
$$g_R(D,A)=\frac{g(D,A)}{H_A(D)}$$
以上讨论都是离散值，如果是连续值呢？

ID3算法:
核心是在决策树各个结点上应用信息增益准则选择信息增益最大且大于阈值的特征，递归地构建决策树.ID3相当于用极大似然法进行概率模型的选择.甶于算法只有树的生成，所以容易产生过拟合。


决策树剪枝策略：
为什么要剪枝：决策树过拟合风险很大，
预剪枝：边建立决策树边进行剪枝的操作
后剪枝：当建立完决策树后进行剪枝操作

代码：

参考代码:

#coding=utf-8
#Author:Dodo
#Date:2018-11-21
#Email:[email protected]
#Blog:www.pkudodo.com
'''
数据集：Mnist
训练集数量：60000
测试集数量：10000
------------------------------
运行结果：ID3(未剪枝)
    正确率：85.9%
    运行时长：356s
'''

import time
import numpy as np

def loadData(fileName):
    '''
    加载文件
    :param fileName:要加载的文件路径
    :return: 数据集和标签集
    '''
    #存放数据及标记
    dataArr = []; labelArr = []
    #读取文件
    fr = open(fileName)
    #遍历文件中的每一行
    for line in fr.readlines():
        #获取当前行，并按“，”切割成字段放入列表中
        #strip：去掉每行字符串首尾指定的字符（默认空格或换行符）
        #split：按照指定的字符将字符串切割成每个字段，返回列表形式
        curLine = line.strip().split(',')
        #将每行中除标记外的数据放入数据集中（curLine[0]为标记信息）
        #在放入的同时将原先字符串形式的数据转换为整型
        #此外将数据进行了二值化处理，大于128的转换成1，小于的转换成0，方便后续计算
        dataArr.append([int(int(num) > 128) for num in curLine[1:]])
        #将标记信息放入标记集中
        #放入的同时将标记转换为整型
        labelArr.append(int(curLine[0]))
    #返回数据集和标记
    return dataArr, labelArr

def majorClass(labelArr):
    '''
    找到当前标签集中占数目最大的标签
    :param labelArr: 标签集
    :return: 最大的标签
    '''
    #建立字典，用于不同类别的标签技术
    classDict = {}
    #遍历所有标签
    for i in range(len(labelArr)):
        #当第一次遇到A标签时，字典内还没有A标签，这时候直接幅值加1是错误的，
        #所以需要判断字典中是否有该键，没有则创建，有就直接自增
        if labelArr[i] in classDict.keys():
            # 若在字典中存在该标签，则直接加1
            classDict[labelArr[i]] += 1
        else:
            #若无该标签，设初值为1，表示出现了1次了
            classDict[labelArr[i]] = 1
    #对字典依据值进行降序排序
    classSort = sorted(classDict.items(), key=lambda x: x[1], reverse=True)
    #返回最大一项的标签，即占数目最多的标签
    return classSort[0][0]

def calc_H_D(trainLabelArr):
    '''
    计算数据集D的经验熵，参考公式5.7 经验熵的计算
    :param trainLabelArr:当前数据集的标签集
    :return: 经验熵
    '''
    #初始化为0
    H_D = 0
    #将当前所有标签放入集合中，这样只要有的标签都会在集合中出现，且出现一次。
    #遍历该集合就可以遍历所有出现过的标记并计算其Ck
    #这么做有一个很重要的原因：首先假设一个背景，当前标签集中有一些标记已经没有了，比如说标签集中
    #没有0（这是很正常的，说明当前分支不存在这个标签）。 式5.7中有一项Ck，那按照式中的针对不同标签k
    #计算Cl和D并求和时，由于没有0，那么C0=0，此时C0/D0=0,log2(C0/D0) = log2(0)，事实上0并不在log的
    #定义区间内，出现了问题
    #所以使用集合的方式先知道当前标签中都出现了那些标签，随后对每个标签进行计算，如果没出现的标签那一项就
    #不在经验熵中出现（未参与，对经验熵无影响），保证log的计算能一直有定义
    trainLabelSet = set([label for label in trainLabelArr])
    #遍历每一个出现过的标签
    for i in trainLabelSet:
        #计算|Ck|/|D|
        #trainLabelArr == i：当前标签集中为该标签的的位置
        #例如a = [1, 0, 0, 1], c = (a == 1): c == [True, false, false, True]
        #trainLabelArr[trainLabelArr == i]：获得为指定标签的样本
        #trainLabelArr[trainLabelArr == i].size：获得为指定标签的样本的大小，即标签为i的样本
        #数量，就是|Ck|
        #trainLabelArr.size：整个标签集的数量（也就是样本集的数量），即|D|
        p = trainLabelArr[trainLabelArr == i].size / trainLabelArr.size
        #对经验熵的每一项累加求和
        H_D += -1 * p * np.log2(p)

    #返回经验熵
    return H_D

def calcH_D_A(trainDataArr_DevFeature, trainLabelArr):
    '''
    计算经验条件熵
    :param trainDataArr_DevFeature:切割后只有feature那列数据的数组
    :param trainLabelArr: 标签集数组
    :return: 经验条件熵
    '''
    #初始为0
    H_D_A = 0
    #在featue那列放入集合中，是为了根据集合中的数目知道该feature目前可取值数目是多少
    trainDataSet = set([label for label in trainDataArr_DevFeature])

    #对于每一个特征取值遍历计算条件经验熵的每一项
    for i in trainDataSet:
        #计算H(D|A)
        #trainDataArr_DevFeature[trainDataArr_DevFeature == i].size / trainDataArr_DevFeature.size:|Di| / |D|
        #calc_H_D(trainLabelArr[trainDataArr_DevFeature == i]):H(Di)
        H_D_A += trainDataArr_DevFeature[trainDataArr_DevFeature == i].size / trainDataArr_DevFeature.size \
                * calc_H_D(trainLabelArr[trainDataArr_DevFeature == i])
    #返回得出的条件经验熵
    return H_D_A

def calcBestFeature(trainDataList, trainLabelList):
    '''
    计算信息增益最大的特征
    :param trainDataList: 当前数据集
    :param trainLabelList: 当前标签集
    :return: 信息增益最大的特征及最大信息增益值
    '''
    #将数据集和标签集转换为数组形式
    #trainLabelArr转换后需要转置，这样在取数时方便
    #例如a = np.array([1, 2, 3]); b = np.array([1, 2, 3]).T
    #若不转置，a[0] = [1, 2, 3]，转置后b[0] = 1, b[1] = 2
    #对于标签集来说，能够很方便地取到每一位是很重要的
    trainDataArr = np.array(trainDataList)
    trainLabelArr = np.array(trainLabelList).T

    #获取当前特征数目，也就是数据集的横轴大小
    featureNum = trainDataArr.shape[1]

    #初始化最大信息增益
    maxG_D_A = -1
    #初始化最大信息增益的特征
    maxFeature = -1
    #对每一个特征进行遍历计算
    for feature in range(featureNum):
        #“5.2.2 信息增益”中“算法5.1（信息增益的算法）”第一步：
        #1.计算数据集D的经验熵H(D)
        H_D = calc_H_D(trainLabelArr)
        #2.计算条件经验熵H(D|A)
        #由于条件经验熵的计算过程中只涉及到标签以及当前特征，为了提高运算速度（全部样本
        #做成的矩阵运算速度太慢，需要剔除不需要的部分），将数据集矩阵进行切割
        #数据集在初始时刻是一个Arr = 60000*784的矩阵，针对当前要计算的feature，在训练集中切割下
        #Arr[:, feature]这么一条来，因为后续计算中数据集中只用到这个（没明白的跟着算一遍例5.2）
        #trainDataArr[:, feature]:在数据集中切割下这么一条
        #trainDataArr[:, feature].flat：将这么一条转换成竖着的列表
        #np.array(trainDataArr[:, feature].flat)：再转换成一条竖着的矩阵，大小为60000*1（只是初始是
        #这么大，运行过程中是依据当前数据集大小动态变的）
        trainDataArr_DevideByFeature = np.array(trainDataArr[:, feature].flat)
        #3.计算信息增益G(D|A)    G(D|A) = H(D) - H(D | A)
        G_D_A = H_D - calcH_D_A(trainDataArr_DevideByFeature, trainLabelArr)
        #不断更新最大的信息增益以及对应的feature
        if G_D_A > maxG_D_A:
            maxG_D_A = G_D_A
            maxFeature = feature
    return maxFeature, maxG_D_A


def getSubDataArr(trainDataArr, trainLabelArr, A, a):
    '''
    更新数据集和标签集
    :param trainDataArr:要更新的数据集
    :param trainLabelArr: 要更新的标签集
    :param A: 要去除的特征索引
    :param a: 当data[A]== a时，说明该行样本时要保留的
    :return: 新的数据集和标签集
    '''
    #返回的数据集
    retDataArr = []
    #返回的标签集
    retLabelArr = []
    #对当前数据的每一个样本进行遍历
    for i in range(len(trainDataArr)):
        #如果当前样本的特征为指定特征值a
        if trainDataArr[i][A] == a:
            #那么将该样本的第A个特征切割掉，放入返回的数据集中
            retDataArr.append(trainDataArr[i][0:A] + trainDataArr[i][A+1:])
            #将该样本的标签放入返回标签集中
            retLabelArr.append(trainLabelArr[i])
    #返回新的数据集和标签集
    return retDataArr, retLabelArr

def createTree(*dataSet):
    '''
    递归创建决策树
    :param dataSet:(trainDataList， trainLabelList) <<-- 元祖形式
    :return:新的子节点或该叶子节点的值
    '''
    #设置Epsilon，“5.3.1 ID3算法”第4步提到需要将信息增益与阈值Epsilon比较，若小于则
    #直接处理后返回T
    #该值的大小在设置上并未考虑太多，观察到信息增益前期在运行中为0.3左右，所以设置了0.1
    Epsilon = 0.1
    #从参数中获取trainDataList和trainLabelList
    #之所以使用元祖作为参数，是由于后续递归调用时直数据集需要对某个特征进行切割，在函数递归
    #调用上直接将切割函数的返回值放入递归调用中，而函数的返回值形式是元祖的，等看到这个函数
    #的底部就会明白了，这样子的用处就是写程序的时候简洁一点，方便一点
    trainDataList = dataSet[0][0]
    trainLabelList = dataSet[0][1]
    #打印信息：开始一个子节点创建，打印当前特征向量数目及当前剩余样本数目
    print('start a node', len(trainDataList[0]), len(trainLabelList))

    #将标签放入一个字典中，当前样本有多少类，在字典中就会有多少项
    #也相当于去重，多次出现的标签就留一次。举个例子，假如处理结束后字典的长度为1，那说明所有的样本
    #都是同一个标签，那就可以直接返回该标签了，不需要再生成子节点了。
    classDict = {i for i in trainLabelList}
    #如果D中所有实例属于同一类Ck，则置T为单节点数，并将Ck作为该节点的类，返回T
    #即若所有样本的标签一致，也就不需要再分化，返回标记作为该节点的值，返回后这就是一个叶子节点
    if len(classDict) == 1:
        #因为所有样本都是一致的，在标签集中随便拿一个标签返回都行，这里用的第0个（因为你并不知道
        #当前标签集的长度是多少，但运行中所有标签只要有长度都会有第0位。
        return trainLabelList[0]

    #如果A为空集，则置T为单节点数，并将D中实例数最大的类Ck作为该节点的类，返回T
    #即如果已经没有特征可以用来再分化了，就返回占大多数的类别
    if len(trainDataList[0]) == 0:
        #返回当前标签集中占数目最大的标签
        return majorClass(trainLabelList)

    #否则，按式5.10计算A中个特征值的信息增益，选择信息增益最大的特征Ag
    Ag, EpsilonGet = calcBestFeature(trainDataList, trainLabelList)

    #如果Ag的信息增益比小于阈值Epsilon，则置T为单节点树，并将D中实例数最大的类Ck
    #作为该节点的类，返回T
    if EpsilonGet < Epsilon:
        return majorClass(trainLabelList)

    #否则，对Ag的每一可能值ai，依Ag=ai将D分割为若干非空子集Di，将Di中实例数最大的
    # 类作为标记，构建子节点，由节点及其子节点构成树T，返回T
    treeDict = {Ag:{}}
    #特征值为0时，进入0分支
    #getSubDataArr(trainDataList, trainLabelList, Ag, 0)：在当前数据集中切割当前feature，返回新的数据集和标签集
    treeDict[Ag][0] = createTree(getSubDataArr(trainDataList, trainLabelList, Ag, 0))
    treeDict[Ag][1] = createTree(getSubDataArr(trainDataList, trainLabelList, Ag, 1))

    return treeDict

def predict(testDataList, tree):
    '''
    预测标签
    :param testDataList:样本
    :param tree: 决策树
    :return: 预测结果
    '''
    # treeDict = copy.deepcopy(tree)

    #死循环，直到找到一个有效地分类
    while True:
        #因为有时候当前字典只有一个节点
        #例如{73: {0: {74:6}}}看起来节点很多，但是对于字典的最顶层来说，只有73一个key，其余都是value
        #若还是采用for来读取的话不太合适，所以使用下行这种方式读取key和value
        (key, value), = tree.items()
        #如果当前的value是字典，说明还需要遍历下去
        if type(tree[key]).__name__ == 'dict':
            #获取目前所在节点的feature值，需要在样本中删除该feature
            #因为在创建树的过程中，feature的索引值永远是对于当时剩余的feature来设置的
            #所以需要不断地删除已经用掉的特征，保证索引相对位置的一致性
            dataVal = testDataList[key]
            del testDataList[key]
            #将tree更新为其子节点的字典
            tree = value[dataVal]
            #如果当前节点的子节点的值是int，就直接返回该int值
            #例如{403: {0: 7, 1: {297:7}}，dataVal=0
            #此时上一行tree = value[dataVal]，将tree定位到了7，而7不再是一个字典了，
            #这里就可以直接返回7了，如果tree = value[1]，那就是一个新的子节点，需要继续遍历下去
            if type(tree).__name__ == 'int':
                #返回该节点值，也就是分类值
                return tree
        else:
            #如果当前value不是字典，那就返回分类值
            return value

def test(testDataList, testLabelList, tree):
    '''
    测试准确率
    :param testDataList:待测试数据集
    :param testLabelList: 待测试标签集
    :param tree: 训练集生成的树
    :return: 准确率
    '''
    #错误次数计数
    errorCnt = 0
    #遍历测试集中每一个测试样本
    for i in range(len(testDataList)):
        #判断预测与标签中结果是否一致
        if testLabelList[i] != predict(testDataList[i], tree):
            errorCnt += 1
    #返回准确率
    return 1 - errorCnt / len(testDataList)

if __name__ == '__main__':
    #开始时间
    start = time.time()

    # 获取训练集
    trainDataList, trainLabelList = loadData('../Mnist/mnist_train.csv')
    # 获取测试集
    testDataList, testLabelList = loadData('../Mnist/mnist_test.csv')

    #创建决策树
    print('start create tree')
    tree = createTree((trainDataList, trainLabelList))
    print('tree is:', tree)

    #测试准确率
    print('start test')
    accur = test(testDataList, testLabelList, tree)
    print('the accur is:', accur)

    #结束时间
    end = time.time()
    print('time span:', end - start)

（五）逻辑回归

定义：

当给定一个训练集（矩阵），如下：

年龄	工资	学历	逾期
20	4000	本科	YES（Y=1）
25	5000	专科	NO（Y=0）
22	6000	本科	NO
28	5000	专科	YES
27	8000	本科

我们需要去预测最后一个人是否会逾期，归根到底就是要学习从输入到输出的映射$f:X\to Y$

最后求出一个条件概率$P(Y|X)$，即$P(Y=1|27，8000，本科)$，其概率大则逾期可能性大，或者说就是比较$P(Y=1|27，8000，本科)$和$P(Y=0|27，8000，本科)$的大小。

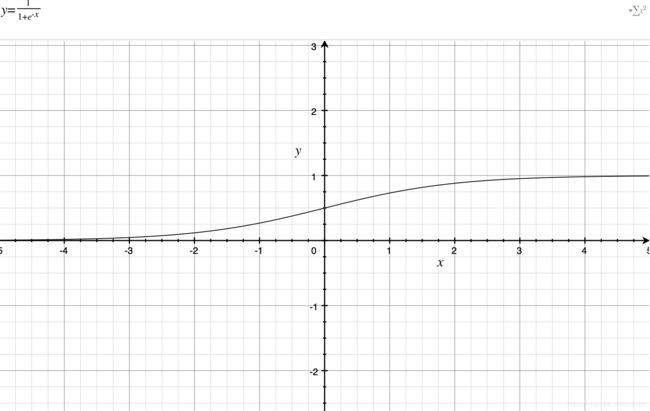
那么能否用线性回归来表示呢？比如：$P(Y=1)=w^{T}x+b$,观察过值域后会发现是不行的，概率不大于1，而右边值域为负无穷到正无穷，为了使得等号成立，则需要采用逻辑函数$\sigma$,$$\sigma (x)=\frac{1}{1+e^{-x}}$$

逻辑函数$\sigma (x)$的值域为$(0,1)$满足概率的值域范围，将$w^{T}x+b$作为自变量替换即可，条件概率即为：

$$P(Y|X)=\frac{1}{1+e^{-(w^T+b)}}$$

对于二分类问题来说：

$$P(Y=1|X)=\frac{1}{1+e^{-w^T+b}}$$

$P(Y=0|X)=\frac{e^{-w^T+b}}{1+e^{-w^T+b}}$

两个式子可以合并为：

$P(y|x,w)=p(y=1|x,w{)}^y[1-p(y=1|x,w)]$

合并的式子可这样理解：当$y=1$时：$p(y=1|x,w)=p(y=1|x,w)\times 1$

当$y=0$时：$p(y=0|x,w)=1-p(y=1|x,w)$

逻辑函数为线性分类器

证明如下：

这是感知机里面的图片，相同的，逻辑回归也是将平面上各种点进行了分类，为了证明逻辑回归是线性的分类器，我们将落在分离平面上的点组成的线方程给求出来，是直线则是线性分类，落在分离平面上的点有一个特点，它到两边的距离都差不多，也就是说它是$y=1$和$y=0$的概率相等：

$$P(Y=1|X)=P(Y=0|X)$$

$$\frac{1}{1+e^{-w^T+b}}=\frac{e^{-w^T+b}}{1+e^{-w^T+b}}$$

推导可得：

$w^{T}x+b=0$

即：分离平面（边界）为线性分类器

逻辑回归的目标函数：

前面已经定义了合并后的：

$$P(y|x,w)=p(y=1|x,w{)}^y[1-p(y=1|x,w){]}^{1-y}$$

下面我们要来由训练集训练出最好的权重$(w)$和偏置$(b)$,从而使得能够最好的拟合我们的数据集$(X)$,因此我们需要最大化：给定样本数据的$x_i,w,b$情况下，对应为label$(y_i)$的概率，也就是条件概率$p(y_i|x_i,w,b)$（最大似然）,想让每一项都最大，那么每个样本条件概率相乘也就最大。

即最大化目标函数：

$$\hat{w},\hat{b}=arma{x}_{w,b}\prod _{i=1}^{n}p(y_i|x_i,w,b)$$（寻找$w,b$使得连乘式最大化）

$$\begin{gathered} arma{x}_{w,b}{\prod }_{i=1}^{n}p(y_i|x_i,w,b) \\ =argma{x}_{w,b}\log ({\prod }_{i=1}^{n}p(y_i|x_i,w,b)) \\ =argma{x}_{w,b}{\sum }_{i=1}^n\log p(y_i|x_i,w,b) \end{gathered}$$

通常我们不喜欢去求最大值，而是转化为最小值求解，即：

$$argmi{n}_{w,b}=-\sum _{i=1}^n\log p(y_i|x_i,w)$$

逻辑回归的梯度下降法：

$$\begin{gathered} argmi{n}_{w,b}-{\sum }_{i=1}^n\log p(y_i|x_i,w) \\ =argmi{n}_{w,b}-{\sum }_{i=1}^n\log p(y_i=1|x,w{)}^{y_i}[1-p(y_i=1|x,w){]}^{1-y_i} \\ =argma{x}_{w,b}-{\sum }_{i=1}^n{y}_i\log p(y_i=1|x,w)+(1-y_i)\log p(y_i=1|x,w) \end{gathered}$$

令$-{\sum }_{i=1}^n{y}_i\log \sigma (w^{T}x+b)+(1-y_i)\log \sigma (w^{T}x+b)$为$L(w,b)$

对权重$w$求导： 求导知识：$\{\begin{array}{l}\sigma (x)=\frac{1}{1+e^{-x}}\\ {\sigma }^{{}^{\prime }}(x)=\sigma (x)[1-\sigma (x)]\\ (\log x{)}^{{}^{\prime }}=\frac{1}{x}\end{array}$

$$\begin{gathered} \frac{\partial L(w,b)}{\partial w}=-{\sum }_{i=1}^n{y}_i\frac{\sigma (w^{T}x+b)[1-\sigma (w^{T}x+b)]}{\sigma (w^{T}x+b)}{x}_i+(1-y_i)\frac{-\sigma (w^{T}x+b)[1-\sigma (w^{T}x+b)]}{1-\sigma (w^{T}x+b)}{x}_i \\ =-{\sum }_{i=1}^n{y}_i[1-\sigma (w^{T}x+b)]x_i+(y_i-1)\sigma (w^{T}x+b)x_i \\ =-{\sum }_{i=1}^n[y_i-\sigma (w^{T}x+b)]x_i \\ ={\sum }_{i=1}^n[\sigma (w^{T}x+b)-y_i]x_i \end{gathered}$$

对偏置$b$求导：

$\frac{\partial L(w,b)}{\partial b}={\sum }_{i=1}^n[\sigma (w^{T}x+b)-y_i]$

（两者相比较，相差一个外部$x_i$相乘）

梯度下降：

初始化$w^1,b^1$

$For：t=1,2...$

​ $$\begin{gathered} w^{t+1}=w^t-\eta {\sum }_{i=1}^n[\sigma (w^{T}x+b)-y_i]x_i \\ {b}^{t+1}=b^t-\eta {\sum }_{i=1}^n[\sigma (w^{T}x+b)-y_i] \end{gathered}$$

梯度下降方式又分为：$\{\begin{array}{l}1.标准梯度下降\\ 2.随机梯度下降\\ 3.Mini-batch梯度下降\end{array}$
标准梯度下降是在权值更新前对所有样例汇总误差,而随机梯度下降的权值是通过考查某个训练样例来更新的，而mini-batch则是两者的折中。

参考博客：
https://www.cnblogs.com/limitlessun/p/8611103.html
https://www.pkudodo.com