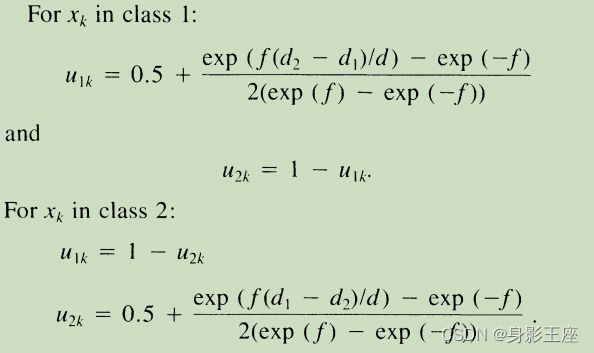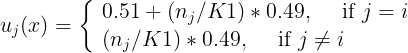A Fuzzy K-Nearest Neighbor Algorithm
0. 论文的基本介绍
Keller J M, Gray M R, Givens J A. A fuzzy k-nearest neighbor algorithm[J]. IEEE transactions on systems, man, and cybernetics, 1985 (4): 580-585.
而且现在这个期刊是一个TOP刊。
1. 摘要
许多算法利用样本之间的距离或相似性作为一种分类手段。在这些模式识别问题中，经常使KNN。但是在KNN中每个样本属于不同类别只有0或1的分别，而每个类别中不同样本属于该类的重要性(隶属度)是不一样的，而KNN中每个标记的样本在同一类中都被赋予同等的重要性，而不管它们的“典型性”如何。通过将模糊集理论引入到KNN中，开发出Fussy_KNN，本文提出了三种对标记样本分配模糊隶属度的方法，并通过实验将Fussy_KNN与传统的KNN(Crips)、其他分类算法进行比较，表明Fussy_KNN具有更好的效果。
2.模糊集
假定n个带有分类标签的样本：
，分类的类别数为c，因此我们可以得到一个隶属度矩阵
，
，
。该隶属度矩阵表示每个样本属于每个类的隶属度(概率)，因此一个样本属于不同类的隶属度之和就为1。
3.KNN算法
3.1 Crisp KNN
假定n个带有分类标签的样本：，该算法流程如下：
Begin
输入一个未知类别样本y
设定k值,1 <= k <= n
初始化 i = 1
DO UNTIL (寻找k个最近的邻居)
计算y到xi的距离
IF (i <= k)
将xi放到k个最近的邻居的数据集中
ELSE IF (y到xi的距离比k个最近的邻居的数据集中的最大值小)
删除k个最近的邻居的数据集中的最大值数据
将xi放到k个最近的邻居的数据集中
END IF
i++
END DO UNTIL
将k个样本中代表的大多数样本的类作为y的类别
IF (如果k个样本中存在多个类样本数并列第一的情况)
计算y与每个类(样本数并列第一)的所有样本距离之和
IF (如果不存在距离和并列第一的情况)
将距离之和最小的类标签作为y的类别
ELSE
将最后发现的距离之和最小的类标签作为y的类别
END IF
ELSE
将样本数最大的类的标签作为y的类别
END IF
END3.2 Fussy K-NN
假定n个带有分类标签的样本：，
表示未知类别样本y属于每个类别的概率(隶属度)。
针对的是n个带有分类标签的样本，它表示的是每个样本属于每个类别的概率(隶属度)。算法流程如下：
Begin
输入一个未知类别样本y
设定k值,1 <= k <= n
初始化 i = 1
DO UNTIL (寻找k个最近的邻居)
计算y到xi的距离
IF (i <= k)
将xi放到k个最近的邻居的数据集中
ELSE IF (y到xi的距离比k个最近的邻居的数据集中的最大值小)
删除k个最近的邻居的数据集中的最大值数据
将xi放到k个最近的邻居的数据集中
END IF
i++
END DO UNTIL
初始化 i = 1
DO UNTIL
计算ui(y)
i++
END DO UNTIL
END
从上述公式我们可以看出，的大小受到两个因素的影响：
- 第一个就是未知样本与标签样本的距离，距离越小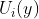，就越大；
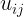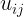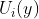- 第二个就是，如果第j个样本在i个类中隶属度越高，越大，就越大。
的设定简单来说有3种：
- 第一种就是属于对应类的设置为1，不属于设置为0；
- 第二种就是根据该样本到类中的所有样本的距离之和来设定；
- 第三种就是类中所有样本求和取均值，然后根据该样本与均值的距离来设定。
m值的设定，m值越大，距离对产生的影响就会缩小。在本文中，m设定为2。
4.最近的原型分类器
4.1 Crisp最近的原型分类器
与上述样本集不同的是，上述每个类别中的每个样本代表一个集合元素，而这里每个集合元素是由一个类别的所有样本的均值组成的。因此这里的样本集表示为
，c代表是类别。因此对应的算法流程如下：
BEGIN
输入待分类的x
初始化 i = 1
DO UNTIL(计算每个类(原型)到x的距离)
计算Zi到x的距离
i++
END DO UNTIL
将距离最小的原型代表的类作为x的类
IF(有并列最小的)
将最后的距离最小的原型代表的类作为x的类
ELSE
将距离最小的原型代表的类作为x的类
END IF
END4.2 Fussy最近的原型分类器
样本集表示为，c代表是类别。因此对应的算法流程如下：
BEGIN
输入待分类的x
初始化 i = 1
DO UNTIL(计算每个类(原型)到x的距离)
计算Zi到x的距离
i++
END DO UNTIL
初始化 i = 1
DO UNTIL
计算ui(x)
i++
END DO UNTIL
END 
5.结果
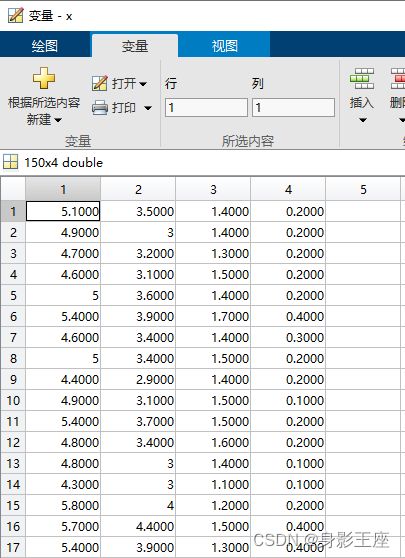
本文中用到的数据集：
该过程是从数据集中保留一个样本，并使用剩余的样本作为标记的数据集对其进行分类。重复这个过程，直到数据集中的所有样本都被分类为止。
本文提出了三种 (带标签样本所属不同类的隶属度)的设定方法：
1、属于对应类的设置为1，不属于设置为0；
2、第二种限制条件是分类的类别只能为2。通过到不同类之间的距离来设定带标签样本所属不同类的隶属度。
这里d1是样本到第1类的平均值的距离，d2是样本到第2类的平均值的距离，d是两个平均值之间的距离(可以设定为(d1+d2)/2)。常数f必须是正的，它控制了隶属度向0.5下降的速率。
3.先找出距离每个带标签样本x最近的k1(不等同于上述的k)个样本，然后每个带标签样本x的各个类的隶属度计算公式如下：
当每个带标签样本x的真正类别i就是j类时候，它在j类中的隶属度值就是上面的计算公式，nj表示k1个最近的样本中属于j类的有多少个样本。当每个带标签样本x的真正类别i不是j类时候，它在j类中的隶属度值就是下面的计算公式，nj表示k1个最近的样本中属于j类的有多少个样本。
以下就是论文中采用3种计算
方法下的Fussy K-NN的实验结果：
这里的1，3，5，7，9指的是计算K1，也就是求的第三种方法种的K1。在大多数KINIT选择中，错误分类的样本类中隶属度高（大于0.8）的错误分类样本的数量远远少于错误分类样本的一半，说明大部分被分类错误的样本是属于类与类之间交接部分的样本。
对比算法的实验效果，用K-Means算法进行分类的结果：
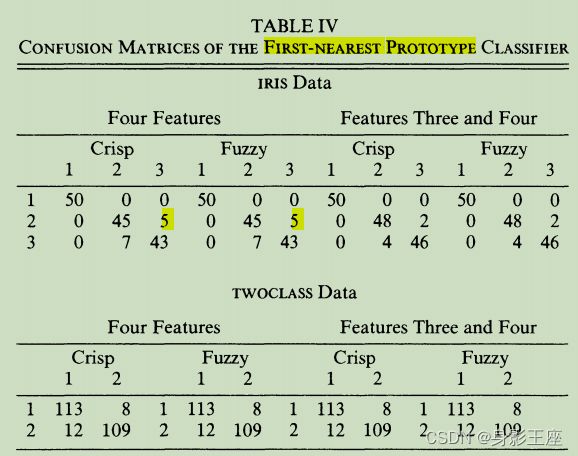
最近原型分类器的实验结果，分为Crisp和Fussy版本：
不同样本的隶属度出现分类错误的情况：
说明大部分被分类错误的样本是属于类与类之间交接部分的样本。
6.算法的复现与实验
6.1Crisp K-NN
y值有1、2、3三类标签。
function test_y = knn(x, y, test_x, k)
% x:nxm,y:nx1,test_x:n0xm,test_y:n0x1
n0 = size(test_x, 1);
test_y = zeros(n0, 1);
for i = 1 : n0
ind = [];
% num表示有多少个类标签
num = 3;
max_label = 0;
Dist = sum((x - test_x(i, :)).^2,2);
% 从小大大排序，取前k个
[D,I] = sort(Dist);
D = D(1:k, :);
D_y = y(I(1:k), :);
for j = 1 : num
% 计算k个样本中各类样本的数量,记录下最大数量的样本的类别
label1 = sum(D_y==j);
if label1 > max_label
max_label = label1;
ind = [];
ind = [ind; j];
elseif label1 == max_label
ind = [ind; j];
end
end
num_ind = size(ind, 1);
min_dist = inf;
% 如果存在数量相等的情况,就将距离之和最小的类标签作为test_y的类别
for j1 = 1 : num_ind
dist = sum(D(D_y == ind(j1)));
if dist <= min_dist
test_y(i, :) = ind(j1);
end
end
end
endclc;clear;clearvars;
load('iris_X.mat', 'iris');
x = iris;
load('iris_Y.mat', 'iris');
y = iris;
n = size(x, 1);
test_y = zeros(n ,1);
for k = 1 : 10
for i = 1 : n
% 在样本集中选择一个样本作为测试集，其他样本作为训练集
test_x = x(i, :);
if i == 1
ind = i + 1 : n;
test_y(i, :) = knn(x(ind, :), y(ind, :), test_x, k);
else
ind = [1 : i - 1, i + 1 : n];
test_y(i, :) = knn(x(ind, :), y(ind, :), test_x, k);
end
end
err_num = sum(test_y ~= y);
err_rate = err_num / n;
fprintf("iris total: %d k: %d err_num: %d err_rate: %.4f\n",n,k,err_num,err_rate);
endclc;clear;clearvars;
load('iris_X.mat', 'iris');
x = iris;
load('iris_Y.mat', 'iris');
y = iris;
n = size(x, 1);
test_y = zeros(n ,1);
for k = 1 : 10
for i = 1 : n
% 在样本集中选择一个样本作为测试集，其他样本作为训练集
test_x = x(i, :);
if i == 1
ind = i + 1 : n;
test_y(i, :) = knn(x(ind, :), y(ind, :), test_x, k);
else
ind = [1 : i - 1, i + 1 : n];
test_y(i, :) = knn(x(ind, :), y(ind, :), test_x, k);
end
end
err_num = sum(test_y ~= y);
err_rate = err_num / n;
fprintf("iris total: %d k: %d err_num: %d err_rate: %.4f\n",n,k,err_num,err_rate);
end 
测试结果与论文中结果差不多，甚至比论文中结果小优。
6.2Fussy K-NN
本文提到了三种计算的方式，根据本文给出的实验结果来看，第三种方式的准确率最高，因此我这里也就只复现第三种计算方式的Fussy K-NN算法。
function u = memberships(x, y, num, k1)
% x:nxm,y:nx1,k1是一个常数,u:n*num,这个num代表类别
n = size(x, 1);
u = zeros(n, num);
for i = 1 : n
ind = [1 : i - 1, i + 1 : n];
Dist = sum((x(ind, :) - x(i, :)).^2,2);
% 从小大大排序，取前k1个
[~,I] = sort(Dist);
D_y = y(I(1:k1), :);
for j = 1 : num
nj = sum(D_y == j);
if y(i, :) == j
u(i, j) = 0.51 + (nj / k1) * 0.49;
else
u(i, j) = (nj / k1) * 0.49;
end
end
end
endfunction test_y = fknn(x, test_x, k, num, u)
% x:nxm,test_x:n0xm,test_y:n0x1,
% u:n*num,这个num代表类别,u->menbershiip,k代表最近邻k个
n0 = size(test_x, 1);
m = 2;
% 表示每个样本属于每个类的概率
U = zeros(n0, num);
for i = 1 : n0
Dist = sum((x - test_x(i, :)).^2,2);
% 从小大大排序，取前k个
[D,I] = sort(Dist);
D = D(1:k, :);
% 防止除0
D(D==0) = 0.00001;
D = D.^(-1 / (m - 1));
Sum_DIST = sum(D);
for j = 1 : num
Sum_MULT = sum(u(I(1:k), j) .* D);
U(i, j) = Sum_MULT / Sum_DIST;
end
end
% 求U每行最大值以及对应的索引
[~, I] = max(U, [], 2);
test_y = I;
end
clc;clear;clearvars;
load('iris_X.mat', 'iris');
x = iris;
load('iris_Y.mat', 'iris');
y = iris;
n = size(x, 1);
% num表示有多少个类标签
num = 3;
for k = 1 : 10
% for k1 = 1 : 5
for k1 = 3
u = memberships(x, y, num, k1);
test_y = zeros(n ,1);
for i = 1 : n
% 在样本集中选择一个样本作为测试集，其他样本作为训练集
test_x = x(i, :);
if i == 1
ind = i + 1 : n;
test_y(i, :) = fknn(x(ind, :), test_x, k, num, u);
else
ind = [1 : i - 1, i + 1 : n];
test_y(i, :) = fknn(x(ind, :), test_x, k, num, u);
end
end
err_num = sum(test_y ~= y);
err_rate = err_num / n;
fprintf("iris total: %d k: %d k1: %d err_num: %d err_rate: %.4f\n",n,k,k1,err_num,err_rate);
end
end
将k1改为5。
最后一次预测的错误的四个值以及相对应的隶属度， 可以看出当隶属度在接近0.5时候，容易预测错误，但是高于0.7后，预测的基本都正确。
6.3The Crisp Nearest Prototype Classifier 和Fuzzy Nearest Prototype Algorithm
The Crisp Nearest Prototype Classifier：
clc;clear;clearvars;
load('iris_X.mat', 'iris');
x = iris;
load('iris_Y.mat', 'iris');
y = iris;
% num表示有多少个类标签
num = 3;
n = size(x, 1);
m = size(x, 2);
z = zeros(num, m);
z_lable = [1; 2; 3];
for i = 1 : num
z(i, :) = sum(x(y == i, :), 1) ./ sum(y == i);
end
% cnp
test_y = zeros(n, 1);
for i = 1 : n
Dist = sum((x(i, :) - z).^2,2);
[~,I] = min(Dist);
test_y(i, :) = I;
end
err_num = sum(test_y ~= y);
fprintf("cnp: iris total: %d err_num: %d\n",n,err_num);
输出：cnp: iris total: 150 err_num: 11
clc;clear;clearvars;
load('iris_X.mat', 'iris');
x = iris;
load('iris_Y.mat', 'iris');
y = iris;
% num表示有多少个类标签
num = 3;
n = size(x, 1);
m = size(x, 2);
z = zeros(num, m);
z_lable = [1; 2; 3];
for i = 1 : num
z(i, :) = sum(x(y == i, :), 1) ./ sum(y == i);
end
U = zeros(n, num);
for i = 1 : n
Dist = sum((x(i, :) - z).^2, 2);
D = Dist.^(-1 / (2 - 1));
Sum_DIST = sum(D);
for j = 1 : num
Sum_MULT = D(j, 1);
U(i, j) = Sum_MULT / Sum_DIST;
end
end
% 求U每行最大值以及对应的索引
[~, test_y] = max(U, [], 2);
err_num = sum(test_y ~= y);
fprintf("fnp: iris total: %d err_num: %d\n",n,err_num);输出：fnp: iris total: 150 err_num: 11
可以看出二者没有本质的差别，错误率差不多。