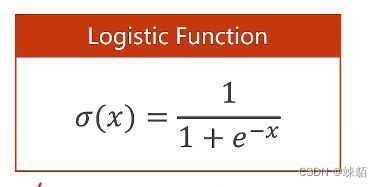《Pytorch深度学习实践》课程合集(刘二大人)笔记
2 线性模型
深度学习步骤
- 数据集 —— 拿到的训练集,要分成两部分,训练集,交叉验证集 和 测试集
- 模型
- 训练
- 推理
ML常用损失函数
模型可视化 visdom包
- 训练过程中,要存盘
- visdom 可视化
'''
线性模型——— 用直线 预测相关的值
'''
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
def forward(x):
return x * w
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) * (y_pred - y)
w_list =[]
mse_list = []
for w in np.arange(0.0, 4.1, 0.1):
print('w=', w)
l_sum = 0
for x_val, y_val in zip(x_data, y_data):
y_pred_val = forward(x_val)
loss_val = loss(x_val, y_val)
l_sum += loss_val
print('\t', x_val, y_pred_val, loss_val)
print("MSE=", l_sum/3)
w_list.append(w)
mse_list.append(l_sum/3)
plt.plot(w_list, mse_list)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()
3 梯度下降
随机梯度下降:随机选一个点
批量梯度下降
import numpy as np
import matplotlib.pyplot as plt
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w=0
def forward(x):
return x*w
def cost (xs, ys):
cost = 0;
for x, y in zip(xs, ys):
y_pred = forward(x)
cost += (y_pred - y) ** 2
return cost/len(xs)
def gradient(xs, ys):
grad = 0
for x,y in zip(xs, ys):
grad += 2*x*(x*w-y)
return grad / len(xs)
print("Predict (before training", 4, forward(4))
for epoch in range(100):
cost_val = cost(x_data, y_data)
grad_val = gradient(x_data, y_data)
w -= 0.01 * grad_val
print('Epoch:',epoch, 'w=',w,'loss=', cost_val)
print('predict(after training', 4, forward(4))
4 反向传播
矩阵的求导公式
matirx cookbook
import torch
x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = torch.tensor([1.0])
w.requires_grad = True
def forward(x):
return x*w
# w is a tensor type variable
def loss(x, y):
y_pred = forward(x)
return (y_pred - y) ** 2
print("predict:", 4, forward(4).item())
for epoch in range(100):
for x, y in zip(x_data, y_data):
l = loss(x,y)
l.backward() # 自动计算梯度,并且反向传播
w.data = w.data - 0.01 * w.grad.data
w.grad.data.zero_()
print("progress:", epoch, l.item())
print("predict", 4, forward(4).item())
5 用pytorch 实现线性回归
确定模型,,定义损失函数,优化损失函数
准备数据集,用类设计模型,,构造损失函数和优化器,,写训练周期(前馈,反馈,更新)
numpy中的自动广播机制
不同维度的矩阵,是不能直接进行加法的
所以,在numpy中,会 把维度小的向量,自动复制成维度大的向量

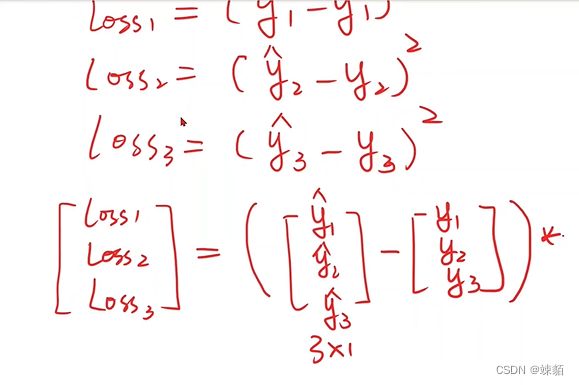
线性单元—— y = w*x+b
函数中传递参数,常用的形式
def func(*args, **kwargs):
print(args)
print(kwargs)
func(1,2,4,3, x=3, y=5)
(1, 2, 4, 3)
{'x': 3, 'y': 5}
*arg : 可以传递很多参数,会进行自动匹配,,结果是一个元组
**kwargs : 是作为一个字典使用
模型训练
#训练模型
for epoch in range(100):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss)
optimizer.zero_grad() # 梯度归0
loss.backward()
optimizer.step()
训练过程,其实就是,先算y_pred, 计算损失函数,,反向传播,,更新参数,四部分组成
import torch
x_data = torch.tensor( [ [1.0], [2.0], [3.0]])
y_data = torch.tensor([[2.0], [4.0], [6.0] ])
class LinearModel(torch.nn.Module):
def __init__(self): #构造函数
super(LinearModel, self).__init__()
self.linear = torch.nn.Linear(1,1)
def forward(self, x):
y_pred = self.linear(x)
return y_pred
model = LinearModel()
# 损失函数
criterion = torch.nn.MSELoss(size_average=False) # false表示不求均值
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
# model.parameters() : 告诉模型,,要对哪些参数进行优化
#训练模型
for epoch in range(100):
y_pred = model(x_data)
loss = criterion(y_pred, y_data)
print(epoch, loss.item())
optimizer.zero_grad() # 梯度归0
loss.backward()
optimizer.step()
print('w=', model.linear.weight.item())
print('b=', model.linear.bias.item())
x_test = torch.tensor([[4.0]])
y_test = model(x_test)
print('y_pred =', y_test.data)