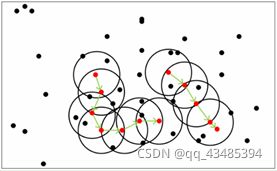
【一个作业】利用高斯混合模型、谱聚类法和DBSCAN进行多维数据聚类
本文目录
- 聚类模型
-
- 高斯混合模型GMM
- 谱聚类
- 密度聚类DBSCAN
- 聚类效果的指标
- 实例:雷达信号分选
-
- 内容
- 代码
- 结果
- 参考
聚类模型
聚类是一种机器学习技术,它涉及到数据点的分组。给定一组数据点,我们可以使用聚类算法将每个数据点划分为一个特定的组。理论上,同一组中的数据点应该具有相似的属性和/或特征,而不同组中的数据点应该具有高度不同的属性和/或特征。聚类是一种无监督学习的方法,是许多领域中常用的统计数据分析技术。
在数据科学中,我们可以使用聚类分析从我们的数据中获得一些有价值的见解。
高斯混合模型GMM
高斯混合模型(Gaussian Mixture Model, GMM):
用概率模型来刻画聚类原型(软聚类)。GMM可以看作是由K个单高斯模型组合而成的模型,即概率密度分布
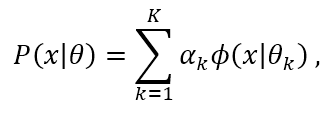 其中, ϕ ( x ∣ θ k ) \mathop{\phi}(x|{\theta}_k) ϕ(x∣θk)为第k个单维高斯分布子模型的概率密度函数,参数为 θ k = ( μ k , σ k 2 , α k ) \mathop{\theta}_k=({\mu}_k,{\sigma}^2_k,{\alpha}_k) θk=(μk,σk2,αk),分别表示每个子模型的期望、方差和混合系数。混合系数 α k \mathop{\alpha}_k αk指的是子模型k在混合模型中发生的概率。
其中, ϕ ( x ∣ θ k ) \mathop{\phi}(x|{\theta}_k) ϕ(x∣θk)为第k个单维高斯分布子模型的概率密度函数,参数为 θ k = ( μ k , σ k 2 , α k ) \mathop{\theta}_k=({\mu}_k,{\sigma}^2_k,{\alpha}_k) θk=(μk,σk2,αk),分别表示每个子模型的期望、方差和混合系数。混合系数 α k \mathop{\alpha}_k αk指的是子模型k在混合模型中发生的概率。
针对GMM的聚类问题,我们采用极大似然估计方法(Maximum Likelihood Estimation, MLE),求解每个子模型的参数 { θ k = ( μ k , σ k 2 , α k ) ∣ k ∈ [ 1 , K ] } \mathop\lbrace{\theta}_k=({\mu}_k,{\sigma}^2_k,{\alpha}_k)|k\in[1,K]\rbrace {θk=(μk,σk2,αk)∣k∈[1,K]}。对于单高斯模型,若每个数据点(个数N)是相互独立的,其对数似然函数为
log L ( θ ) = ∑ j = 1 N log ϕ ( x j ∣ θ ) . \begin{aligned} \log L({\theta}) = {\sum}_{j=1}^{N}\log \phi(x_j|\theta). \end{aligned} logL(θ)=∑j=1Nlogϕ(xj∣θ).
对于GMM,其对数似然函数为
log L ( θ ) = ∑ j = 1 N ∑ k = 1 K α k ϕ ( x ∣ θ k ) . \begin{aligned} \log L({\theta}) = {\sum}_{j=1}^{N}{\sum}_{k=1}^K\alpha_k\phi(x|\theta_k). \end{aligned} logL(θ)=∑j=1N∑k=1Kαkϕ(x∣θk).
对于上述求似然函数最大的问题,由于每个子分布是未知的,即隐遍历,我们常用EM算法(Expectation-Maximization)求解各个参数。EM算法的每次迭代包含两个步骤,即E步和M步:
① E步:
根据当前参数计算每个样本j来自子模型k的后验概率
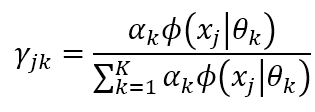 其中, j = 1 , 2 , … , N , k = 1 , 2 , … , K \mathop j=1,2,…,N,k=1,2,…,K j=1,2,…,N,k=1,2,…,K。
其中, j = 1 , 2 , … , N , k = 1 , 2 , … , K \mathop j=1,2,…,N,k=1,2,…,K j=1,2,…,N,k=1,2,…,K。
② M步:
若 { θ k = ( μ k , σ k 2 , α k ) ∣ k ∈ [ 1 , K ] } \mathop\lbrace{\theta}_k=({\mu}_k,{\sigma}^2_k,{\alpha}_k)|k\in[1,K]\rbrace {θk=(μk,σk2,αk)∣k∈[1,K]}能使似然函数最大,则分别对三个函数求偏导更新参数:
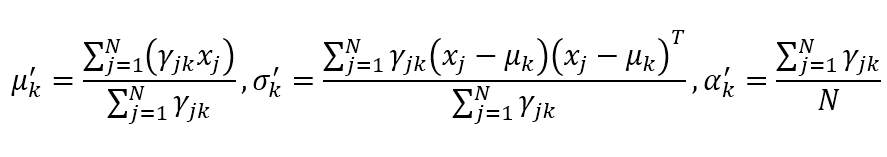 其中, k = 1 , 2 , … , K \mathop k=1,2,…,K k=1,2,…,K。当停止条件满足时,停止迭代。
其中, k = 1 , 2 , … , K \mathop k=1,2,…,K k=1,2,…,K。当停止条件满足时,停止迭代。
谱聚类
谱聚类(spectral clustering),是一种基于图论的聚类方法。。它的主要思想是把所有的数据看做空间中的点,这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低,而距离较近的两个点之间的边权重值较高,通过对所有数据点组成的图进行切图,让切图后不同的子图间边权重和尽可能的低,而子图内的边权重和尽可能的高,从而达到聚类的目的。
因此,概括来说,谱聚类的步骤主要有两个,一是构图,二是切图。构图时,样本对应的是图的顶点,样本相似度是边的权重。切图后的结果是同子图内顶点相似度高,不同子图内顶点相似度低。
谱聚类的主要步骤 :
- 根据样本构建权重矩阵 W。
- 计算度矩阵 D 和拉普拉斯矩阵 L,对 L 进行奇异值分解(SVD);
- 取 L 的前 K 个最小特征值对应的右奇异向量,构成矩阵 V。这一步的目的是给拉普拉斯特征映射降维度。
- 对 V 的行向量进行K-Means聚类。即对样本数据的拉普拉斯矩阵的奇异值向量进行聚类。
密度聚类DBSCAN
DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于一组“邻域”参数来刻画样本分布的紧密程度的密度聚类方式。它是从样本密度的角度考察样本之间的可连接性,将簇定义为密度相连的点的最大集合,能够把具有足够高密度的区域划分为簇,并可在噪声的空间数据库中发现任意形状的聚类。
DBSCAN划分簇的方法为:若 x \mathop x x为核心对象,由 x \mathop x x密度可达的所有样本组成的集合为X,则 X 即为满足连接性与最大性的簇。其中,密度可达表示:
若 x j \mathop x_j xj位于 x i \mathop x_i xi的 ϵ \mathop \epsilon ϵ - 邻域中,且 x i \mathop x_i xi是核心对象,那么称 x j \mathop x_j xj由 x i \mathop x_i xi密度直达。那么,若有一连串这样的 ( x n , x n − 1 , . . . , x 0 ) \mathop (x_n,x_{n-1},...,x_0) (xn,xn−1,...,x0),其中, x i \mathop x_i xi由 x i − 1 \mathop x_{i-1} xi−1密度直达,那么 x n \mathop x_n xn由 x 0 \mathop x_0 x0密度可达。
聚类效果的指标
1.精度
精度(accuracy)表示聚类后,分选正确的样本数占样本总数的比例。
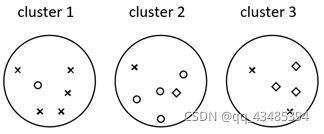
2.聚类纯度
聚类纯度(Purity),利用聚类后的每个簇中,占比最高的真实类别的元素个数计算。由于对于聚类后的结果我们并不知道每个簇所对应的真实类别,因此需要取每种情况下的最大值。具体的,纯度的计算公式定义如下:
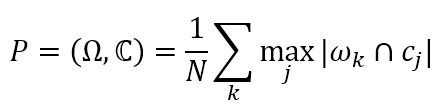 其中, N \mathop N N表示总的样本数。 Ω = { ω 1 , ω 2 , . . . , ω K } \mathop \Omega = \lbrace \omega_1,\omega_2,...,\omega_K\rbrace Ω={ω1,ω2,...,ωK}表示聚类后的簇和集合, C = { c 1 , c 2 , . . . , c J } \mathop C = \lbrace c_1,c_2,...,c_J\rbrace C={c1,c2,...,cJ}表示正确的类别。 ω k \mathop \omega_k ωk表示聚类后第 k \mathop k k个簇中所有的样本,而 c j \mathop c_j cj表示第 j \mathop j j个类真实的样本。
其中, N \mathop N N表示总的样本数。 Ω = { ω 1 , ω 2 , . . . , ω K } \mathop \Omega = \lbrace \omega_1,\omega_2,...,\omega_K\rbrace Ω={ω1,ω2,...,ωK}表示聚类后的簇和集合, C = { c 1 , c 2 , . . . , c J } \mathop C = \lbrace c_1,c_2,...,c_J\rbrace C={c1,c2,...,cJ}表示正确的类别。 ω k \mathop \omega_k ωk表示聚类后第 k \mathop k k个簇中所有的样本,而 c j \mathop c_j cj表示第 j \mathop j j个类真实的样本。
3.混淆矩阵
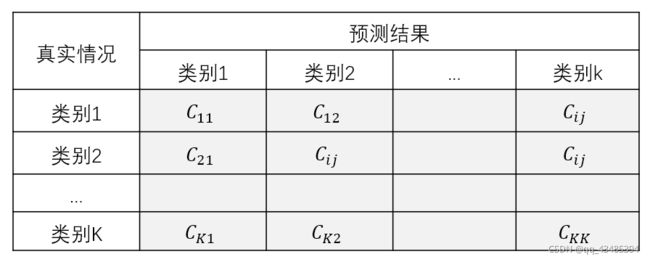
混淆矩阵可以用于评估分类的准确性。根据定义,混淆矩阵如下灰色区域所示,其中 C i j \mathop C_{ij} Cij等于已知在簇i中,被预测为簇 j \mathop j j中的样本数量。
…
实例:雷达信号分选
即,利用上述三种聚类方法分类雷达信号辐射源。
内容
假设环境中包含 8 部雷达,每部雷达的数据参数如下:
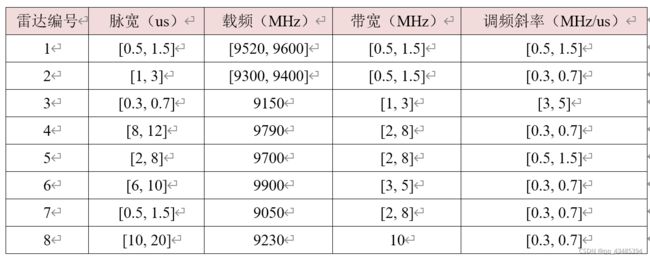
对给出的 8 部雷达数据实现基于无监督聚类的信号分选,具体步骤为:
- 针对每部雷达,在其各参数区间内随机产生 500 个样本数据,每个样本包含上述四种特征数据(脉宽、载频、带宽和调频斜率);
- 分别用 GMM、谱聚类、DBSCAN 三种算法进行聚类分选;
- 列表比较各算法的以下指标:精度、聚类纯度、辐射源级的查准率和查全率;
- 列表比较各算法的效率。
补充:辐射源级的查准率和查全率
对于信号分选,有时我们只关心是否能将电磁环境中存在的各个辐射源分选出来,也就是考察“辐射源级”的信号分选结果,而不会关注到“样本级”的粒度。
对于单个辐射源级的查准率(Precision)和查全率(Recall)定义如下:
① 查准率(Precision):分选出的信息中我们关注的辐射源的信号的比例。
② 查全率(Recall):我们关注的辐射源信号有多少比例被分选出来了。
代码
代码如下:
1.生成数据
import openpyxl
import numpy as np
import xlrd
import random
''' 函数2 产生的样本数据写入excel表格'''
def write_to_excel(value,sheet_name,filename):
# 雷达数据i = [脉宽,载频,带宽,调频斜率]*500
wb = openpyxl.load_workbook(filename)
sheet = wb[sheet_name]
for item in value:
sheet.append(item)
wb.save(filename)
print('成功!')
''' 函数1 由雷达参数产生随机数据 '''
def sample_data(radar_para, N, Num):
[Tl, Tu, fcl, fcu, Bl, Bu, Kl, Ku] = radar_para
sample = []
for i in range(N):
T = np.random.uniform(Tl,Tu)
fc = np.random.uniform(fcl,fcu)
B = np.random.uniform(Bl,Bu)
K = np.random.uniform(Kl,Ku)
sample.append([T,fc,B,K,Num]) # Num是标签,无监督时用不上
return sample
# 读取雷达参数,也就是上文的那个表格
para_excel = xlrd.open_workbook('parameter.xlsx')
para_sheet = para_excel.sheet_by_name('radar')
nRows = para_sheet.nrows # 读取行数
nRadar = nRows -1
radar_para = [] # 雷达参数list
for i in range(nRows-1):
para = para_sheet.row_values(i+1)
radar_para.append(para[1::])
print(para)
# 每个雷达的信号数据个数
N = 500
# 建立用于存放数据的excel表格
filename = 'radar_data.xlsx'
wb = openpyxl.Workbook()
sheet_name = 'data'
wb.create_sheet(sheet_name,0)
sheet = wb[sheet_name]
heads = ['脉宽','载频','带宽','调频斜率','标签']
sheet.append(heads)
wb.save(filename)
# 向excel写数据
data = []
for i in range(nRadar):
shuju = sample_data(radar_para[i],N,i)
data = data + shuju
write_to_excel(data,sheet_name,filename) # 生成一个excel hxd!
2.聚类
以DBSCAN为例.
准确率,辐射源级的查全率和查准率就不在这里写了。
这几个参数的计算需要进行标签映射:因为无监督聚类后,虽然本质上的同一类可能大部分都分到了一起,但是他的标签与原标签不一定是对应的。
标签映射需要设计一个简单的算法
这里可以说一下我个人的思路:看一下每个聚类得到的簇里面哪个真实类别最多,就把该类标记为哪个真实类别。
import time
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import DBSCAN
from sklearn import metrics
#----------------- Subfunction -------------------
def normalization(data): # 数据归一化
_range = np.max(data) - np.min(data)
return (data - np.min(data)) / _range
begin_time = time.time() # 测试运行时间
# 自设颜色
colors = [] # 你喜欢的颜色~
radar_data_sheet = pd.read_excel('样本数据文件路径')
[x, y] = radar_data_sheet.shape
radar_data = radar_data_sheet[radar_data_sheet.columns[0:y-1]].values
radar_label = radar_data_sheet[radar_data_sheet.columns[-1]].values
# 对数据归一化处理 谱聚类不用归一化
radar_data_norm = normalization(radar_data)
#------------------- 模型 ------------------------
db = DBSCAN(eps=0.005, min_samples=10) # DBSCAN
label_pred = db.fit_predict(radar_data_norm)
print(label_pred==-1)
# GMM
# gmm = GaussianMixture(
# n_components = num_clusters, covariance_type="full", max_iter=20)
# gmm.fit(radar_data_norm)
# label_pred = gmm.predict(radar_data_norm) # 训练得到的label
# 谱聚类
#sp = SpectralClustering(n_clusters=num_clusters,
# assign_labels='discretize',
# random_state=0)
#label_pred = sp.fit_predict(X) # 得到预测的 lable
#------------------- 聚类性能指标 ---------------------
print("簇数: %d" % num_clusters)
print("Completeness: %0.3f" % metrics.completeness_score(radar_label, label_pred))
print("Homogeneity: %0.3f" % metrics.homogeneity_score(radar_label, label_pred))
# 准确率还有查准率和查全率就不在这里写了
#---------------------- 绘图 -----------------------
plt.figure(1)
plt.figure(figsize=(10, 8))
# 原图
plt.subplot(2,2,1)
plt.title('Original data')
for i in range(num_clusters):
data = radar_data[radar_label == i]
plt.scatter(data[:, 0],data[:, 1],s=2, color= colors[i])
plt.subplot(2,2,3)
plt.title('Original data')
for i in range(num_clusters):
data = radar_data[radar_label == i]
plt.scatter(data[:, 2], data[:, 3], s=2, color=colors[i])
# 绘制聚类后的图
plt.subplot(2,2,2)
plt.title('DBSCAN')
for i in range(num_clusters):
data = radar_data[label_pred == i]
plt.scatter(data[:, 0],data[:, 1],s=2, color= colors[i])
plt.subplot(2,2,4)
plt.title('DBSCAN')
for i in range(num_clusters):
data = radar_data[label_pred == i]
plt.scatter(data[:, 2], data[:, 3], s=2, color=colors[i])
end_time = time.time()
run_time = end_time-begin_time
print ('DBSCAN 程序运行时间:',run_time)
结果
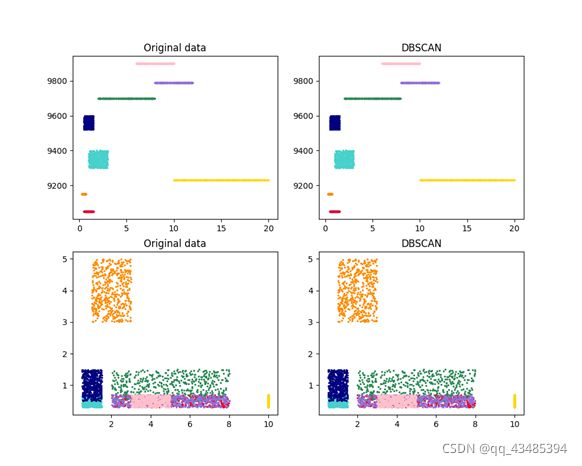
簇数: 8
准确率: 100.00%
Completeness: 1.000
Homogeneity: 1.000
DBSCAN 程序运行时间: 1.3269813867223123
参考
[1] 五种主要聚类算法
[2] sklearn官网