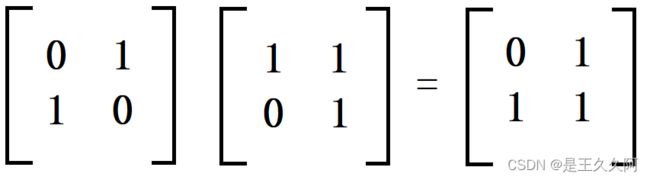2.C语言矩阵乘法

目录

1.原理

左乘和右乘

乘法原理

2.C语言编写矩阵乘法函数

编写函数（数组形式和指针形式）

测试

3.完整代码

---

1.原理

左乘和右乘

在线性代数中，矩阵左乘和矩阵右乘是不一样的。

例如：现有矩阵A： ，矩阵B：。

AB为矩阵B左乘矩阵A：

BA为矩阵B右乘矩阵A：

通过计算发现：左乘和右乘的结果是完全不同的，所以在进行矩阵乘法时，需分清左乘和右乘。

乘法原理

矩阵乘法需要满足的条件：左侧矩阵的列数=右侧矩阵的行数。

结果矩阵的行和列：行数=左侧矩阵的行数，列数=右侧矩阵的列数。

矩阵的相乘过程：

以AB为例：

• A矩阵的第一行中的元素和B矩阵第一列中的元素对应相乘再相加，结果放在第一行第一列中；
• A矩阵的第一行中的元素和B矩阵第二列中的元素对应相乘再相加，结果放在第一行第二列中；
• A矩阵的第一行中的元素和B矩阵第三列中的元素对应相乘再相加，结果放在第一行第三列中；
• ......
• A矩阵的第三行中的元素和B矩阵第三列中的元素对应相乘再相加，结果放在第三行第三列中；

最后的结果为：

2.C语言编写矩阵乘法函数

编写函数（数组形式和指针形式）

矩阵虽然有左乘和右乘之分，但是只要更改传入参数的位置，即可实现左乘和右乘。

核心思想：

• 利用二维数组将矩阵中的数存放起来，用define定义行和列的数值，方便代码的更改。
• 定义一个矩阵左乘函数Matrix_left_mul，将矩阵以及矩阵的行列长度传给函数。
• 利用3个for循环遍历完成计算。

传参的时候可以用数组的形式传，也可以用指针的形式传，二者本质都一样。两种方法都会进行介绍。

1、我们创建两个数组arr1和arr2来存放两个矩阵

（在平时创建二维数组时，不能省略列，可以省略行；但是在矩阵乘法中，行和列的信息都要有）

//左矩阵的行和列
#define COL1 4  
#define ROW1 3
//右矩阵的行和列
#define ROW2 4
#define COL2 3
double arr1[ROW1][COL1] = { 1,2,3,4,5,6,7,8,9,10,11,12};
double arr2[ROW2][COL2] = { 12,11,10,9,8,7,6,5,4,3,2,1};

2、传参以及判断矩阵相称的条件是否成立

利用assert断言条件是否成立，如果不成立系统会提示报错，assert需要包含头文件。

因为数组传参传的是地址，所以函数的类型设置为void即可。

如果不进行判断，传入错误的参数后，二维数组的访问会溢出，返回一个随机数。

数组形式：

void Matrix_left_mul(double arr1[][COL1], double arr2[][COL2], double arr3[][COL2],int row1,int row2,int col1,int col2)
{
	assert(col1 == row2);//判定左列是否等于右行，需包含头文件
	
}

指针形式： 

void Matrix_left_mul(double(*arr1)[COL1], double (*arr2)[COL2], double(*arr3)[COL2], int row1, int row2, int col1, int col2)
{
	assert(col1 == row2);//判定左列是否等于右行，assert需包含头文件
}

3、for循环遍历计算

创建三个for循环：

• 第一个for循环（i）：循环左矩阵的i行
• 第二个for循环（j）：循环右矩阵的j列
• 第三个for循环（k）：逐个循环左行k元素×右列k元素，将其结果累加

数组形式：

int i = 0;//行
int j = 0;//列
int k = 0;//行列中，第k个元素相乘
for (i = 0; i < row1; i++)//从第i行开始
{
	for (j = 0; j < col2; j++)//从第j列开始
	{
		for (k = 0; k < col1; k++)//i行元素和j列元素相乘，结果累加
		{
			arr3[i][j] += arr1[i][k] * arr2[k][j];
		}
	}
}

指针形式：

void Matrix_left_mul(double(*arr1)[COL1], double (*arr2)[COL2], double(*arr3)[COL2], int row1, int row2, int col1, int col2)
{
	assert(col1 == row2);//判定左列是否等于右行，assert需包含头文件
	int i = 0;//行
	int j = 0;//列
	int k = 0;//行列中，第k个元素相乘
	for (i = 0; i < row1; i++)//从第i行开始
	{
		for (j = 0; j < col2; j++)//从第j列开始
		{
			for (k = 0; k < col1; k++)//i行元素和j列元素相乘，结果累加
			{
				*(* (arr3 + i)+j) += *(*(arr1 + i) + k) * *(*(arr2 +k) + j);
			}
		}
	}
}

用define定义常量的优点就是灵活，方便使用，后续只需要更改输入矩阵的相关参数即可进行运算。

测试

在VS中，F10进入调试模式，监视arr1，arr2，arr3数组。这里为了监视方便，我们暂时将数组改成整型，数组中的参数都是整数。

 结果完全正确，如果不放心还可以多试验几组数据。

3.完整代码

数组形式：

#include
#include

//左矩阵的行和列
#define COL1 4  
#define ROW1 3
//右矩阵的行和列
#define ROW2 4
#define COL2 3

void Matrix_left_mul(double arr1[][COL1], double arr2[][COL2], double arr3[][COL2],int row1,int row2,int col1,int col2)
{
	assert(col1 == row2);//判定左列是否等于右行，assert需包含头文件
	int i = 0;//行
	int j = 0;//列
	int k = 0;//行列中，第k个元素相乘
	for (i = 0; i < row1; i++)//从第i行开始
	{
		for (j = 0; j < col2; j++)//从第j列开始
		{
			for (k = 0; k < col1; k++)//i行元素和j列元素相乘，结果累加
			{
				arr3[i][j] += arr1[i][k] * arr2[k][j];
			}
		}
	}
}

int main()
{
	double arr1[ROW1][COL1] = { 1,2,3,4,5,6,7,8,9,10,11,12};
	double arr2[ROW2][COL2] = { 12,11,10,9,8,7,6,5,4,3,2,1 };
	double arr3[ROW1][COL2]={0};//结果矩阵的行等于左矩阵的行，列等于右矩阵的列
    Matrix_left_mul(arr1, arr2, arr3,ROW1,ROW2,COL1,COL2);
	return 0;
}

指针形式

#include
#include

//左矩阵的行和列
#define COL1 4  
#define ROW1 3
//右矩阵的行和列
#define ROW2 4
#define COL2 3

void Matrix_left_mul(double(*arr1)[COL1], double (*arr2)[COL2], double(*arr3)[COL2], int row1, int row2, int col1, int col2)
{
	assert(col1 == row2);//判定左列是否等于右行，assert需包含头文件
	int i = 0;//行
	int j = 0;//列
	int k = 0;//行列中，第k个元素相乘
	for (i = 0; i < row1; i++)//从第i行开始
	{
		for (j = 0; j < col2; j++)//从第j列开始
		{
			for (k = 0; k < col1; k++)//i行元素和j列元素相乘，结果累加
			{
				*(* (arr3 + i)+j) += *(*(arr1 + i) + k) * *(*(arr2 +k) + j);
			}
		}
	}
}

int main()
{
	double arr1[ROW1][COL1] = { 1,2,3,4,5,6,7,8,9,10,11,12 };
	double arr2[ROW2][COL2] = { 12,11,10,9,8,7,6,5,4,3,2,1 };
	double arr3[ROW1][COL2] = { 0 };//结果矩阵的行等于左矩阵的行，列等于右矩阵的列
	Matrix_left_mul(arr1, arr2, arr3, ROW1, ROW2, COL1, COL2);
	return 0;
}