元学习入门必备:MAML(背景+论文解读+代码分析)
文章目录
- 前言
- 背景
-
- 元学习简介
- 元学习问题定义
- 小样本学习(Few shot learning)
-
- 问题定义
- 元学习/小样本学习基本特征
- 论文解读
-
- Abstract
- Introduction
- Motivation
- Model-Agnostic Meta-Learning
-
- 元学习问题设定
- 与模型无关的元学习算法
-
- 细节
- 伪代码
- 算法实例讲解
- 实验部分
- MAML vs Pre-training
- 代码分析
-
- 代码总体结构图
- 数据加载
- 网络构建
-
- forward 模块
- 网络训练
- 主函数
- 总结
前言
就在今年三四月份,炒出了一个“元宇宙”的新名词,相信大家并不陌生吧,百度百科的解释:“元宇宙(Metaverse)是利用科技手段进行链接与创造的,与现实世界映射与交互的虚拟世界,具备新型社会体系的数字生活空间。说起来比较遥远,跟我们目前现实并不是特别直观,但是元学习(Meta Learning)这个概念已经被提出了很多年了,让我们一探究竟吧。
今天给大家分享一篇比较经典的文章,也是入门元学习的必看论文:MAML
论文题目:Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks
模型不可知元学习在深度网络快速自适应中的应用
论文是2017年发表在ICML上的,目前被引用量也超过4600+,值得大家进行学习。
背景
元学习简介
在我前一篇文章已经介绍过元学习的一些基本概念和与机器学习的区别,大家感兴趣的话可以看一下MetaSelector:基于用户级自适应模型选择的元学习推荐
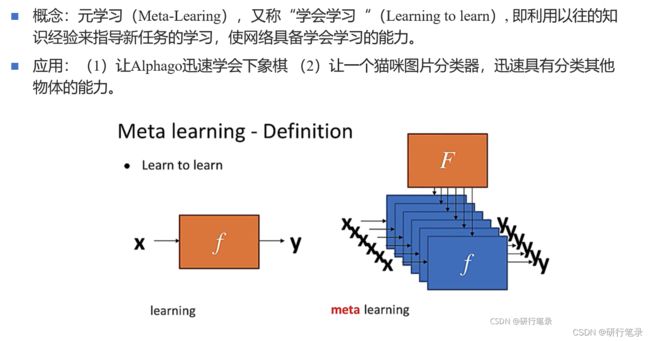
元学习问题定义
下面就是将元学习定义为双层优化问题,这是一个新思路,希望能够对元学习有更深刻的理解。

首先将元训练集分为支持集(Support)和查询集(Query);w可以看成算法;θ可以认为是模型参数;
在内层优化阶段(Inner loop),在支持集中,采用w算法,根据task的loss值表现,来进行优化θ参数,最终根据Ltask最小值,内层优化得到最优的θ’值。
在外层优化阶段(Outer loop),在查询集中,根据内层优化的最优θ’值,计算当前Lmeta的值,根据多个任务后,计算出最小的所有任务的总loss值来优化w参数,不断调整w算法,最终在所有任务中表现最优。
根据双层优化的思想,我们可以将元学习问题也是可以定义为一个双层优化的问题。
小样本学习(Few shot learning)
问题定义
人类非常擅长通过极少量的样本识别一个新物体,比如小孩子只需要书中的一些图片就可以认识什么是“斑马”,什么是“犀牛”。在人类的快速学习能力的启发下,研究人员希望机器学习模型在学习了一定类别的大量数据后,对于新的类别,只需要少量的样本就能快速学习,这就是 Few-shot Learning 要解决的问题。
通俗理解:在训练阶段模型学习大量数据,在测试阶段通过少量的样本学习后,可以快速的学习样本特征。
元学习/小样本学习基本特征
论文解读
Abstract
通过论文题目,我们会有一个大致的了解,Model-Agnostic(模型无关)、Fast Adaptation(快速适应)、Deep Networks(深度网络),可以看出这篇文章是适用于深度网络并且提出一种与模型无关的通用框架。
主要内容:提出了一种与模型无关的元学习算法,它与任何用梯度下降训练的模型都是兼容的,并且适用于各种不同的学习问题【分类、回归和强化学习】
元学习的目标:训练一个关于各种学习任务的模型,这样就可以只使用少量的训练样本来解决新的学习任务。
具体方法:模型的参数被显式地训练,使得少量的梯度步长和来自新任务的少量训练数据将在该任务上产生良好的泛化性能。
实验结果:证明了该方法在两个少镜头图像分类基准上的最优性能。
Introduction
关键思想是训练模型的初始参数,使模型在通过一个或多个用来自新任务的少量数据计算的一个或多个梯度步骤更新参数后,在新任务上具有最大的性能。
从特征学习的观点来看,训练模型的参数使得几个梯度步骤,甚至单个梯度步骤就可以在新任务上产生良好结果的过程可以被视为构建广泛适用于许多任务的内部表示,如果内部表示适用于许多任务,只需稍微微调参数(例如,主要通过修改前馈模型中的顶层权重)就可以产生良好的结果。
我们的程序针对易于微调和快速调整的模型进行了优化,允许在适合快速学习的空间进行调整。
从动力系统的观点来看,我们的学习过程可以被视为最大化新任务的损失函数对参数的敏感度:敏感度较高时,对参数的微小局部更改可导致深度网络快速适应的模型不可知元学习在任务损失方面的大幅改善。
这项工作的主要贡献是一种简单的与模型和任务无关的元学习算法,该算法训练模型的参数,以便少量的梯度更新将导致在新任务上的快速学习。
Motivation

传统的模型就是随机初始化,这样一开始的参数需要很多步更新后才能够达到比较好的结果。所以在MAML中想要获得一个比较好的初始值他和她,只经过一步更新后,就能够获得对于当前任务比较好的参数。【我们可以看右边的图,θ根据三个loss值得到对应的更新方向,最终经过一步更新后,获得一个比较好的初始值,适用于其他任务。】
Model-Agnostic Meta-Learning
训练能够实现快速适应的模型,这是一种经常被形式化为极少机会学习的问题设置。
元学习问题设定
小样本学习中常见的一个概念:N-way N-shot
N-way 的意思是N分类
N-shot是在学习的样本中,每个类只提供N个样本
例子:常见小样本学习分类数据集MiniImagenet,5-way 5-shot
小样本元学习的目标:训练一个只使用几个数据点和训练迭代就能快速适应新任务的模型。
实现目标:在一组任务的元学习阶段对模型或学习者进行训练,使得训练的模型可以仅使用少量的示例或试验来快速适应新的任务。
为了实现这一点,相当于定义一个模型 f ,使得对于输入的X任务,会产生a. 我们训练这个网络使得它可以适应不同的无限的任务。 f ( x ) = a f(x)=a f(x)=a
在图像分类中,其中L()是损失函数,q()是样本的分布,定义公式:
T = { L ( x 1 , a 1 ) , q ( x 1 ) } T=\left\{L\left(x_{1}, a_{1}\right), q\left(x_{1}\right)\right\} T={L(x1,a1),q(x1)}
主要过程:从P(T)任务分布中选取新任务T,在k-shot的情境下,使用k个样本训练模型,从q()分布中选取k个样本,生成对应任务T的L().
与模型无关的元学习算法
细节
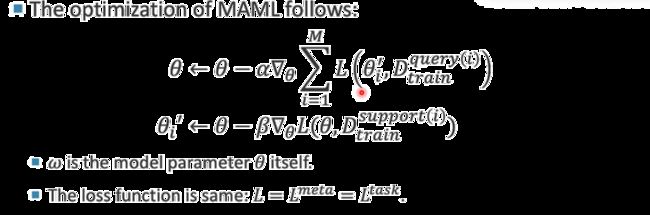
根据上述元学习的背景中,MAML算法的具体细节正如上图所示。首先进入内层优化,在支持集中,根据当前的θ值情况,进行一步更新得到θ’,经过内层优化后得到较好的θ’后,在外层优化查询集中,根据在查询集中θ’的loss值情况,在进行外层的θ更新,最终得到一个较好的θ初始值。
与元学习不同的点是:1、w值就是θ值本身 2:同时Ltask和Lmeta的Loss设计是一致的。
伪代码

上图是MAML的伪代码,下面就小曾哥就继续带大家一起来分析
1、首先随机初始化θ值
2、然后从P(T)中取出任务Ti
3、进入内层优化,根据当前初始化的θ值,评估梯度变化,然后进行一步更新,得到更新后的θi’值。
4、继续再从P(T)中取出其他任务Ti
5、然后根据更新后的θi’,在查询集中计算loss值,最后根据所有任务的loss值之和来进行更新θ值情况。
上述是MAML算法的基本流程,有助于帮助大家理解。
算法实例讲解
1、简图1
左边部分还是算法伪代码,右边是帮助大家加深理解,通过实例来讲解。
首先我们选择两个任务,分别是bird和deer分类器,定义为task1和task2
然后我们在内部优化的过程中,选择支持集进行第一步θ更新,我们发现,φt1是任务1的更新方向,φt2是任务2的更新方向,完成内部优化过程。

2、简图2
我们可以看到右边出现了对应task1和task2的test图片,对应的是任务的查询集,我们现在就进行外部优化,可以看到,通过查询集,我们也能够计算当前更新后的θ’值的梯度变化,分别是图片中的蓝色和红色线。

3、简图3
那么最关键的部分就在右边,我们θ值为什么会有一个比较好的初始化?
可以看到我们的θ更新,是根据任务1和任务2的梯度变化来进行更新的,那么θ到底是从哪个地方来更新呢?这也是一个比较简单的向量合并,可以看到蓝色线和红色线,最终θ是朝着绿色线更新,对应前面还有一个系数,因此就是紫色线部分,这条紫线就是任务1和任务2的最好的θ初始值。

实验部分

可以看到在回归的任务中,MAML进行一步更新的绿色线通过5个样本点能够与ground truth趋势保持一致,在10个样本点的情况下,表现的效果更好。

在分类的任务中,MAML的性能跟其他方法相比效果还是比较好的。
MAML vs Pre-training
相信有很多小伙伴感觉MAML跟预训练比较相似,都是想给模型一个比较好的初始参数。下面就介绍一下MAML和Pre-training的区别
 在这里插入图片描述
在这里插入图片描述
这个图片是吴恩达老师视频里面的,可以看到的区别是Loss函数的定义,在Pre-training里面,是想要获得当前的loss值最小的θ就好。而在MAML中,其实是获得进行一步更新后的θ’情况,然后再取得最小的Loss值对应的θ’值。其实可以任务,预训练更注重当前的表现如何,而MAML则是更注重表现潜力如何。
通俗理解:MAML中的θ可以认为是教练,θ’是教练教的学员,在比赛中,是学员上场,所以教练技术好不好不是那么重要,而是要让教出的学员表现的比较好就行了。而预训练更像是要求教练表
现的比较好,那么学员表现的也比较好。
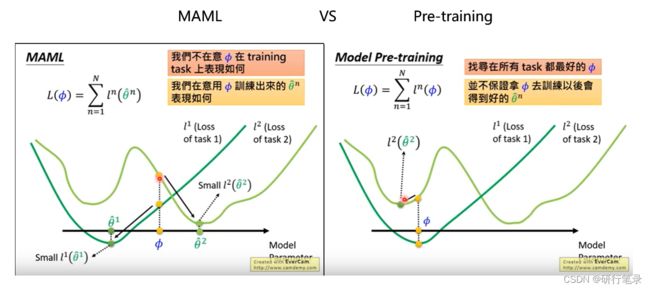
相信这张图,应该很多小伙伴都看过吧,这个也是比较直观的凸显出MAML算法的优势
1、首先看左边MAML这张图,一开始的φ再中间点,在两个任务中都不太好,但是根据一次更新后,可以看到都到达每个任务的最低点,已经能够达到全局最优。
2、然后看右边Pre-training这张图,一开始的φ是在两个任务中loss之和的最小值,可以认为是相对较好,但是经过一步更新后,任务2更新到绿色点,可以发现只是一个局部最优的情况,并不能达到右边全局最优点。
通过上图,应该能够更加直观知道MAML和Pre-training之间的区别。
代码分析
关于MAML的代码,论文里面提供的github链接是tensflow版本,如果需要看Pytorch版本,可以访问MAML pytorch 版本代码
传统的深度学习实现框架步骤
(1)要先定义好网络,(2)然后从数据集中随机取出一个batch送入网络中,(3)最后通过输出结果与真实结果之间的误差,更新参数。
(1)和(2)都各自需要继承pytorch中的某一个定制类。所谓定制类,就是类中有一些特殊的函数,我们继承这些类,就必须要针对自己的算法实现这些特殊函数,我们把这些函数实现好了,(1)和(2)代码这块就已经结束。
代码总体结构图

【这块也是看了知乎大佬的讲解,感兴趣的可以直达链接:https://zhuanlan.zhihu.com/p/343827171】
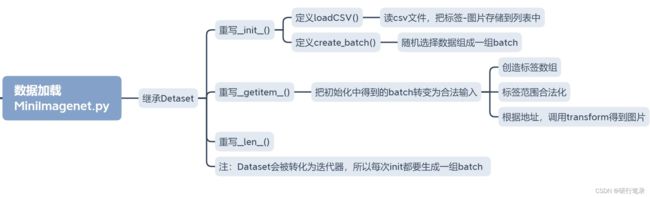
数据加载
针对从网络上下载好数据集,(1)从这一数据集中随机取出一组数据组成一个batch,(2)把得到的batch转变为合法输入,具体来说,要得到能直接送进神经网络中的张量。
数据加载需要继承torch.utils.data.Dataset类,通过继承它,再在主函数配合以torch.utils. data.DataLoader,就可以定义出一个迭代器。随后,在每一次主函数的训练中都会从这个迭代器中取出一个batch的数据,送到神经网络中训练。
网络构建
实现神经网络前向传播的整个过程,搭建好后,输入数据,就可以得到结果。
如果要用pytorch定义自已的网络,就一定要继承torch.nn.Module类,它是专门为神经网络设计的模块化接口,nn.Module是nn中十分重要的类, 包含网络各层的定义及forward方法。

forward 模块
MAML算法的核心思想,就是forward这块,就是定义输入数据是如何在网络中前向传播的。
下面就具体进行这块的代码分析
# 完整代码
def forward(self, x_spt, y_spt, x_qry, y_qry):
"""
:param x_spt: [b, setsz, c_, h, w]
:param y_spt: [b, setsz]
:param x_qry: [b, querysz, c_, h, w]
:param y_qry: [b, querysz]
:return:
"""
task_num, setsz, c_, h, w = x_spt.size()
querysz = x_qry.size(1)
losses_q = [0 for _ in range(self.update_step + 1)] # losses_q[i] is the loss on step i
corrects = [0 for _ in range(self.update_step + 1)]
for i in range(task_num):
# 1. run the i-th task and compute loss for k=0
logits = self.net(x_spt[i], vars=None, bn_training=True)
loss = F.cross_entropy(logits, y_spt[i])
grad = torch.autograd.grad(loss, self.net.parameters())
fast_weights = list(map(lambda p: p[1] - self.update_lr * p[0], zip(grad, self.net.parameters())))
# this is the loss and accuracy before first update
with torch.no_grad():
# [setsz, nway]
logits_q = self.net(x_qry[i], self.net.parameters(), bn_training=True)
loss_q = F.cross_entropy(logits_q, y_qry[i])
losses_q[0] += loss_q
pred_q = F.softmax(logits_q, dim=1).argmax(dim=1)
correct = torch.eq(pred_q, y_qry[i]).sum().item()
corrects[0] = corrects[0] + correct
# this is the loss and accuracy after the first update
with torch.no_grad():
# [setsz, nway]
logits_q = self.net(x_qry[i], fast_weights, bn_training=True)
loss_q = F.cross_entropy(logits_q, y_qry[i])
losses_q[1] += loss_q
# [setsz]
pred_q = F.softmax(logits_q, dim=1).argmax(dim=1)
correct = torch.eq(pred_q, y_qry[i]).sum().item()
corrects[1] = corrects[1] + correct
for k in range(1, self.update_step):
# 1. run the i-th task and compute loss for k=1~K-1
logits = self.net(x_spt[i], fast_weights, bn_training=True)
loss = F.cross_entropy(logits, y_spt[i])
# 2. compute grad on theta_pi
grad = torch.autograd.grad(loss, fast_weights)
# 3. theta_pi = theta_pi - train_lr * grad
fast_weights = list(map(lambda p: p[1] - self.update_lr * p[0], zip(grad, fast_weights)))
logits_q = self.net(x_qry[i], fast_weights, bn_training=True)
# loss_q will be overwritten and just keep the loss_q on last update step.
loss_q = F.cross_entropy(logits_q, y_qry[i])
losses_q[k + 1] += loss_q
with torch.no_grad():
pred_q = F.softmax(logits_q, dim=1).argmax(dim=1)
correct = torch.eq(pred_q, y_qry[i]).sum().item() # convert to numpy
corrects[k + 1] = corrects[k + 1] + correct
# end of all tasks
# sum over all losses on query set across all tasks
loss_q = losses_q[-1] / task_num
# optimize theta parameters
self.meta_optim.zero_grad()
loss_q.backward()
# print('meta update')
# for p in self.net.parameters()[:5]:
# print(torch.norm(p).item())
self.meta_optim.step()```
首先我们 通过代码进入for循环里面,选择一个任务i
1、主要进行梯度计算,得到一步更新后的梯度fast_weight
logits = self.net(x_spt[i], vars=None, bn_training=True)
loss = F.cross_entropy(logits, y_spt[i])
grad = torch.autograd.grad(loss, self.net.parameters())
fast_weights = list(map(lambda p: p[1] - self.update_lr * p[0], zip(grad, self.net.parameters())))
这里介绍更新前的loss和准确度情况
特别注意 self.net(x_qry[i], self.net.parameters(), bn_training=True),输入是更新前的参数
2、这里介绍更新前的loss和准确度情况
特别注意 self.net(x_qry[i], self.net.parameters(), bn_training=True),是更新前的参数self.net.parameters()
with torch.no_grad():
# [setsz, nway]
logits_q = self.net(x_qry[i], self.net.parameters(), bn_training=True)
loss_q = F.cross_entropy(logits_q, y_qry[i])
losses_q[0] += loss_q
pred_q = F.softmax(logits_q, dim=1).argmax(dim=1)
correct = torch.eq(pred_q, y_qry[i]).sum().item()
corrects[0] = corrects[0] + correct
3、计算更新后的loss和准确度情况
特别注意logits_q = self.net(x_qry[i], fast_weights, bn_training=True)中,参数是fast_weights,是更新后的梯度参数
with torch.no_grad():
logits_q = self.net(x_qry[i], fast_weights, bn_training=True)
loss_q = F.cross_entropy(logits_q, y_qry[i])
losses_q[1] += loss_q
# [setsz]
pred_q = F.softmax(logits_q, dim=1).argmax(dim=1)
correct = torch.eq(pred_q, y_qry[i]).sum().item()
corrects[1] = corrects[1] + correct
4、计算任务的loss值,以及更新后一次的梯度,然后计算更新后的loss_q值,保存下来
for k in range(1, self.update_step):
# 1. run the i-th task and compute loss for k=1~K-1
logits = self.net(x_spt[i], fast_weights, bn_training=True)
loss = F.cross_entropy(logits, y_spt[i])
# 2. compute grad on theta_pi
grad = torch.autograd.grad(loss, fast_weights)
# 3. theta_pi = theta_pi - train_lr * grad
fast_weights = list(map(lambda p: p[1] - self.update_lr * p[0], zip(grad, fast_weights)))
logits_q = self.net(x_qry[i], fast_weights, bn_training=True)
# loss_q will be overwritten and just keep the loss_q on last update step.
loss_q = F.cross_entropy(logits_q, y_qry[i])
losses_q[k + 1] += loss_q
with torch.no_grad():
pred_q = F.softmax(logits_q, dim=1).argmax(dim=1)
correct = torch.eq(pred_q, y_qry[i]).sum().item() # convert to numpy
corrects[k + 1] = corrects[k + 1] + correct
5、最后进行梯度更新θ参数
loss_q = losses_q[-1] / task_num
# optimize theta parameters
self.meta_optim.zero_grad()
loss_q.backward()
self.meta_optim.step()
网络训练
要实现神经网络反向传播的整个过程,搭建好后,输入有标签数据,就能更新神经网络参数。
首先会在__init__()中,实例化上一小节创建的神经网络类net=learner()
其次会在forward()中,先喂数据给net,进行正向传播,再根据结果,结合MAML算法,进行反向传播,更新参数。
主函数
总结
这篇文章很早就已经写了一部分了,主要是想把这个MAML更具体一点,不仅有元学习的背景知识,还有MAML论文的解析,加上具体代码实现,将理论与实践进行结合,是入门元学习的不二之选,如果对大家有所帮助,还请点个赞,收藏,评论,在此谢谢大家。
关于代码解析的部分,感兴趣的可以直达链接:https://zhuanlan.zhihu.com/p/343827171


