GRNN和PNN神经网络简介与MATLAB实践

目录

GRNN（广义回归神经网络）

PNN（概率神经网络）

RBF、GRNN、PNN总结对比

MATLAB实例：鸢尾花种类识别

---

GRNN（广义回归神经网络）和PNN（概率神经网络），与RBF非常的相似，请先看上一篇博文《简单直白理解RBF神经网络及其MATLAB实例》，了解一下RBF的大致原理。本文介绍将类比RBF神经网络来介绍。

GRNN（广义回归神经网络）

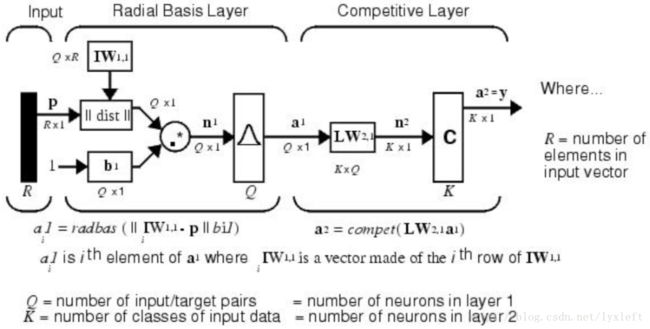
我们先看上面的示意图。左边的部分（input层和径向基层）和RBF神经网络非常相似，都是比较输入和训练集的欧氏距离，经过RBF的激活函数得到一个输出（a1），然后进入右边的线性处理部分，做一个连接权值、线性方程组求解的过程。LW{2，1}也是一个确定的结果，用的是训练集的输出矩阵（T），再和输出a1做点乘（nprod）。

这么讲可能有点抽象。我们知道一般RBF函数，中间对称轴处x=0处对应的y=1，即如果横轴的值||dist||接近0时，输出为1。假设有个输入向量p非常接近于训练集样本中某个样本。则p产生的第一层的输出a1接近于1，由于第二层的权重LW{2，1}就是设为T（T是target，就是训练集的输出），则第二层的输出a2也会与等于1乘以T，就是T的值。

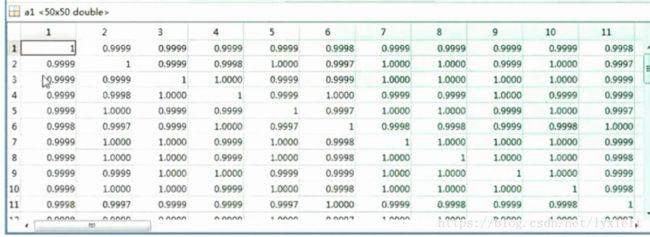
上述现象，可以在matlab中查看a1矩阵的值来帮助理解，我们会发现对角线的元素都是1：

为什么？因为p1作为测试样本时，和p1最接近；p2作为测试样本时，和p2最接近……每个样本作为测试样本输入时，总会和自己最接近，输出就会是1。

matlab中GRNN的函数是：net = newgrnn(P,T,spread)，我们可以通过MATLAB的文档来学习一下GRNN的知识：

P	R-by-Q matrix of Q input vectors
T	S-by-Q matrix of Q target class vectors
spread	Spread of radial basis functions (default = 1.0)

如何调参数spread：The larger the spread, the smoother the function approximation. To fit data very closely, use a spread smaller than the typical distance between input vectors. To fit the data more smoothly, use a larger spread.（调整spread直接影响到的是偏置b）

续上面那张a1矩阵的值的图，如果此时调整spread参数，调整的更大，会怎么样？

我们就会发现所有值都接近于1。

GRNN的性质：

newgrnn creates a two-layer network. The first layer has radbas neurons, and calculates weighted inputs with dist and net input with netprod. The second layer has purelin neurons, calculates weighted input with normprod, and net inputs with netsum. Only the first layer has biases.

newgrnn sets the first layer weights to P', and the first layer biases are all set to 0.8326/spread, resulting in radial basis functions that cross 0.5 at weighted inputs of +/– spread. The second layer weights W2 are set to T.

正因为GRNN没有权值这一说，所以不用训练的优势就体现在他的速度真的很快。而且曲线拟合的非常自然。样本精准度不如径向基精准，但在实际测试中表现甚至已经超越了BP。

 

PNN（概率神经网络）

PNN和RBF、GRNN很相似，只是第二层最后输出时，不是用线性函数（加权和，线性映射），而是成了竞争层（只是取出一个最大的样本对应的label作为结果）！

MATLAB函数：net = newpnn(P,T,spread)

P	R-by-Q matrix of Q input vectors
T	S-by-Q matrix of Q target class vectors
spread	Spread of radial basis functions (default = 0.1)

If spread is near zero, the network acts as a nearest neighbor classifier. As spread becomes larger, the designed network takes into account several nearby design vectors.

newpnn creates a two-layer network. The first layer has radbas neurons, and calculates its weighted inputs with dist and its net input with netprod. The second layer has compet neurons, and calculates its weighted input with dotprod and its net inputs withnetsum. Only the first layer has biases.

newpnn sets the first-layer weights to P', and the first-layer biases are all set to 0.8326/spread, resulting in radial basis functions that cross 0.5 at weighted inputs of +/– spread. The second-layer weights W2 are set to T.

RBF、GRNN、PNN总结对比

RBF网络是一个三层的网络，出了输入输出层之外仅有一个隐层。隐层中的转换函数是局部响应的高斯函数，而其他前向型网络，转换函数一般都是全局响应函数。由于这样的不同，要实现同样的功能，RBF需要更多的神经元，这就是rbf网络不能取代标准前向型网络的原因。但是RBF的训练时间更短。它对函数的逼近是最优的，可以以任意精度逼近任意连续函数。隐层中的神经元越多，逼近越较精确. 径向基神经元和线性神经元可以建立广义回归神经网络，它是径RBF网络的一种变化形式，经常用于函数逼近。在某些方面比RBF网络更具优势。 径向基神经元和竞争神经元还可以组成概率神经网络。PNN也是RBF的一种变化形式，结构简单训练快捷，特别适合于模式分类问题的解决。

MATLAB实例：鸢尾花种类识别

%% I. 清空环境变量
clear all
clc

%% II. 训练集/测试集产生
%%
% 1. 导入数据
load iris_data.mat

%%
% 2 随机产生训练集和测试集
P_train = [];
T_train = [];
P_test = [];
T_test = [];
for i = 1:3
    temp_input = features((i-1)*50+1:i*50,:);
    temp_output = classes((i-1)*50+1:i*50,:);
    n = randperm(50);
    % 训练集――120个样本
    P_train = [P_train temp_input(n(1:40),:)'];
    T_train = [T_train temp_output(n(1:40),:)'];
    % 测试集――30个样本
    P_test = [P_test temp_input(n(41:50),:)'];
    T_test = [T_test temp_output(n(41:50),:)'];
end

%% III. 模型建立 
result_grnn = [];
result_pnn = [];
time_grnn = [];
time_pnn = [];
for i = 1:4
    for j = i:4
        p_train = P_train(i:j,:);
        p_test = P_test(i:j,:);
       %% 
        % 1. GRNN创建及仿真测试
        t = cputime;
        % 创建网络
        net_grnn = newgrnn(p_train,T_train);
        % 仿真测试
        t_sim_grnn = sim(net_grnn,p_test);
        T_sim_grnn = round(t_sim_grnn);
        t = cputime - t;
        time_grnn = [time_grnn t];
        result_grnn = [result_grnn T_sim_grnn'];
       %%
        % 2. PNN创建及仿真测试
        t = cputime;
        Tc_train = ind2vec(T_train);
        % 创建网络
        net_pnn = newpnn(p_train,Tc_train);
        % 仿真测试
        Tc_test = ind2vec(T_test);
        t_sim_pnn = sim(net_pnn,p_test);
        T_sim_pnn = vec2ind(t_sim_pnn);
        t = cputime - t;
        time_pnn = [time_pnn t];
        result_pnn = [result_pnn T_sim_pnn'];
    end
end

%% IV. 性能评价
%%
% 1. 正确率accuracy
accuracy_grnn = [];
accuracy_pnn = [];
time = [];
for i = 1:10
    accuracy_1 = length(find(result_grnn(:,i) == T_test'))/length(T_test);
    accuracy_2 = length(find(result_pnn(:,i) == T_test'))/length(T_test);
    accuracy_grnn = [accuracy_grnn accuracy_1];
    accuracy_pnn = [accuracy_pnn accuracy_2];
end

%%
% 2. 结果对比
result = [T_test' result_grnn result_pnn]
accuracy = [accuracy_grnn;accuracy_pnn]
time = [time_grnn;time_pnn]

%% V. 绘图
figure(1)
plot(1:30,T_test,'bo',1:30,result_grnn(:,4),'r-*',1:30,result_pnn(:,4),'k:^')
grid on
xlabel('测试集样本编号')
ylabel('测试集样本类别')
string = {'测试集预测结果对比(GRNN vs PNN)';['正确率:' num2str(accuracy_grnn(4)*100) '%(GRNN) vs ' num2str(accuracy_pnn(4)*100) '%(PNN)']};
title(string)
legend('真实值','GRNN预测值','PNN预测值')
figure(2)
plot(1:10,accuracy(1,:),'r-*',1:10,accuracy(2,:),'b:o')
grid on
xlabel('模型编号')
ylabel('测试集正确率')
title('10个模型的测试集正确率对比(GRNN vs PNN)')
legend('GRNN','PNN')
figure(3)
plot(1:10,time(1,:),'r-*',1:10,time(2,:),'b:o')
grid on
xlabel('模型编号')
ylabel('运行时间(s)')
title('10个模型的运行时间对比(GRNN vs PNN)')
legend('GRNN','PNN')

 

参考资料：

1、Wasserman, P.D., Advanced Methods in Neural Computing, New York, Van Nostrand Reinhold, 1993, pp. 155–61

2、MATLAB文档

3、概率神经网络（PNN）https://blog.csdn.net/guoyunlei/article/details/76209647

4、https://blog.csdn.net/qq_18343569/article/details/47071423