RBF神经网络、GRNN广义回归神经网络、PNN概率神经网络

RBF神经网络介绍

• RBF神经网络能够逼近任意的非线性函数

  RBF可以处理系统内部难以解析的规律性，具有良好的泛化能力，并有很快的学习收敛速度，已成功应用于非线性函数逼近、时间序列分析、数据分类、模式识别、信息处理、系统建模、控制和故障诊断。

• RBF网络收敛速度快

  当网络的可调参数（权值或阈值）对任何一个输出都有影响时，该网络称为全局逼近网络；
  对于每一次输入，网络上的各个权值都要调整，从而导致网络学习速度很慢；例如BP神经网络

  如果对于输入空间的某个局部区域只有少数几个连接权值影响输出，则该网络称为局部逼近网络；例如RBF神经网络，可有效提高学习速度。

RBF网络结构

• RBF网络是一种三层前向型网络，如下图：
  

  • 输入层由信号源结点组成；

  • 第二层为隐含层，隐含层神经元数目视所描述问题的需要而定（示例中隐含层神经元p个），隐含层神经元的传递函数是对中心点径向对称且衰减的非负非线性函数

  • 第三层为输出层，它对输入模式的作用做出响应

  • 从输入空间到隐含层空间的变换是非线性的，而从隐含层空间到输出层空间的变换是线性的。

RBF隐藏层

• 径向基函数

  • 径向基函数是一个取值仅仅依赖离原点距离的实值函数

  • 函数公式：$radbas(X,C)=\varphi (||X-C||)$，表示x到任意一点c的距离，c点称为中心点；由于距离是径向的，称为径向基函数。$||X-C||$表示差向量的模，或者叫2范数

  • 径向基函数:
    Guass（高斯）函数：$\Phi (x)=\exp (-\frac{x^2}{{\sigma }^2})$，$\sigma$称为径向基函数的扩展常数，它反映了函数图像的宽度，$\sigma$越小，宽度越窄，函数越具有选择性
    

• 基于径向基函数的插值函数：
  $F(x)={\sum }_{p=1}^p{w}_p{\varphi }_p(||X-X^p||)=w_1{\varphi }_1(||X-X^p||)+w_2{\varphi }_2(||X-X^p||)+\dots \dots +w_p{\varphi }_p(||X-X^p||)$
  

  RBF的方法是为隐藏层选择P个基函数，每个基函数对应一个训练数据，各基函数形式为${\varphi }_p(||X-X^p||)$；

• 隐藏层作用

  • 输入X是个m维的向量，样本容量为P，P>m。可以看到输入数据点$X^p$是径向基函数${\varphi }_p$的中心。

  • 隐藏层的作用是把向量从低维映射到高维，低维线性不可分的情况到高维就线性可分了

RBF神经网络MATLAB代码

%% I. 清空环境变量
clear all
clc

%% II. 训练集/测试集产生
%%
% 1. 导入数据
load spectra

%%
% 2. 随机产生训练集和测试集
temp = randperm(size(NIR,1));
% 训练集——50个样本
P_train = NIR(temp(1:50),:)';
T_train = octane(temp(1:50),:)';
% 测试集——10个样本
P_test = NIR(temp(51:end),:)';
T_test = octane(temp(51:end),:)';
N = size(P_test,2);

%% III. RBF神经网络创建及仿真测试
%%
% 1. 创建网络
net = newrbe(P_train,T_train,30);

%%
% 2. 仿真测试
T_sim = sim(net,P_test);

%% IV. 性能评价
%%
% 1. 相对误差error
error = abs(T_sim - T_test)./T_test;

%%
% 2. 决定系数R^2
R2 = (N * sum(T_sim .* T_test) - sum(T_sim) * sum(T_test))^2 / ((N * sum((T_sim).^2) - (sum(T_sim))^2) * (N * sum((T_test).^2) - (sum(T_test))^2)); 

%%
% 3. 结果对比
result = [T_test' T_sim' error']

%% V. 绘图
figure
plot(1:N,T_test,'b:*',1:N,T_sim,'r-o')
legend('真实值','预测值')
xlabel('预测样本')
ylabel('辛烷值')
string = {'测试集辛烷值含量预测结果对比';['R^2=' num2str(R2)]};
title(string)

GRNN广义回归神经网络

• GRNN网络结构

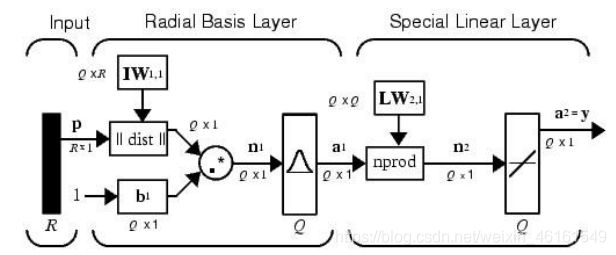
  如下图所示：GRNN一般由输入层、隐含层和输出层组成；

  输入层仅将样本变量送入隐含层，并不参与真正的运算；

  隐含层的神经元个数等于训练集样本数，该层的权值函数为欧式距离函数(||dist||表示)，其作用为计算网络输入与第一层的权值$I{W}_{1,1}$之间的距离，$b_1$为隐含层的阈值。隐含层的传递函数为径向基函数，通常采用高斯函数作为网络的传递函数。

  输出层的权函数为规范化点积权函数（用nprod表示），计算网络的向量为$n^2=normprod[L{W}_{2,1}{a}^1]$，它的每个元素就是向量$a^1=radbas(||I{W}_{1,1}-p||b_1)$和权值矩阵$L{W}_{2,1}$(取训练集输出矩阵)每行元素的点积再除以向量$a^1$的铬元素之和得到的，并将结果$n^2$提供给线性传递函数$a^2=purelin(n^2)$，计算网络的输出。
  

• 与BP神经网络相比，GRNN具有以下优点：

  网络的训练是单个训练而不需要迭代；

  隐含层神经元个数由训练样本自适应确定；

  网络各层之间的连接权重由训练样本唯一确定，避免了BP神经网络在迭代中的权值修改；

  隐含层节点的激活函数采用对输入信息具有局部激活特性的高斯函数，使得对接近于局部神经元特征德尔输入具有很强的吸引力

PNN概率神经网络

• Parzen方法

  由高斯函数为基函数来形成联合概率密度分布的估计方法和贝叶斯优化规则，构造了一种概率密度分类估计和并行处理的神经网络。

• PNN结构
  
  如上图所示：

  与GRNN类似，PNN由输入层、隐藏层及输出层组成；

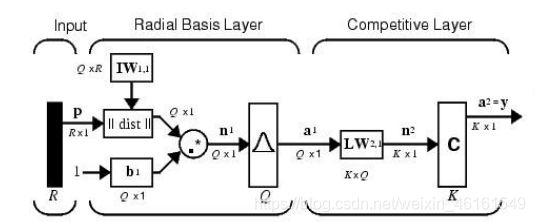
  与GRNN不同的是，PNN的输出层采用竞争输出代替线性输出，$a^2=compet(L{W}_{2,1}{a}^1)$，各神经元只依据Parzen方法来求和估计估计各类的概率，从而竞争输入模式的响应机会，最后仅有一个神经元竞争获胜，这样获胜神经元即表示对输入模式的分类。

• 特点
  PNN既具有一般神经网络所具有的特点，又具有很好的泛化能力及快速学习能力

  数学角度看PNN结构：Cover定理证明，对于一个模式问题，在高维数据空间中可能解决在低维空间不易解决的问题。PNN隐含层神经元的个数表示隐含层的空间维数，维数越高，网络的逼近精度就越高，同时网络复杂程度也会增加。

GRNN和PNN MATLAB代码

%% I. 清空环境变量
clear all
clc

%% II. 训练集/测试集产生
%%
% 1. 导入数据
load iris_dataset

%%
% 2 随机产生训练集和测试集
P_train = [];
T_train = [];
P_test = [];
T_test = [];
for i = 1:3
    temp_input = features((i-1)*50+1:i*50,:);
    temp_output = classes((i-1)*50+1:i*50,:);
    n = randperm(50);
    % 训练集——120个样本
    P_train = [P_train temp_input(n(1:40),:)'];
    T_train = [T_train temp_output(n(1:40),:)'];
    % 测试集——30个样本
    P_test = [P_test temp_input(n(41:50),:)'];
    T_test = [T_test temp_output(n(41:50),:)'];
end

%% III. 模型建立 
result_grnn = [];
result_pnn = [];
time_grnn = [];
time_pnn = [];
for i = 1:4
    for j = i:4
        p_train = P_train(i:j,:);
        p_test = P_test(i:j,:);
       %% 
        % 1. GRNN创建及仿真测试
        t = cputime;
        % 创建网络
        net_grnn = newgrnn(p_train,T_train);	% spread默认为1
        % 仿真测试
        t_sim_grnn = sim(net_grnn,p_test);
        T_sim_grnn = round(t_sim_grnn);
        t = cputime - t;
        time_grnn = [time_grnn t];
        result_grnn = [result_grnn T_sim_grnn'];
       %%
        % 2. PNN创建及仿真测试
        t = cputime;
        Tc_train = ind2vec(T_train);
        % 创建网络
        net_pnn = newpnn(p_train,Tc_train);
        % 仿真测试
        % Tc_test = ind2vec(T_test);
        t_sim_pnn = sim(net_pnn,p_test);
        T_sim_pnn = vec2ind(t_sim_pnn);
        t = cputime - t;
        time_pnn = [time_pnn t];
        result_pnn = [result_pnn T_sim_pnn'];
    end
end

%% IV. 性能评价
%%
% 1. 正确率accuracy
accuracy_grnn = [];
accuracy_pnn = [];
time = [];
for i = 1:10
    accuracy_1 = length(find(result_grnn(:,i) == T_test'))/length(T_test);
    accuracy_2 = length(find(result_pnn(:,i) == T_test'))/length(T_test);
    accuracy_grnn = [accuracy_grnn accuracy_1];
    accuracy_pnn = [accuracy_pnn accuracy_2];
end

%%
% 2. 结果对比
result = [T_test' result_grnn result_pnn]
accuracy = [accuracy_grnn;accuracy_pnn]
time = [time_grnn;time_pnn]

%% V. 绘图
figure(1)
plot(1:30,T_test,'bo',1:30,result_grnn(:,4),'r-*',1:30,result_pnn(:,4),'k:^')
grid on
xlabel('测试集样本编号')
ylabel('测试集样本类别')
string = {'测试集预测结果对比(GRNN vs PNN)';['正确率:' num2str(accuracy_grnn(4)*100) '%(GRNN) vs ' num2str(accuracy_pnn(4)*100) '%(PNN)']};
title(string)
legend('真实值','GRNN预测值','PNN预测值')
figure(2)
plot(1:10,accuracy(1,:),'r-*',1:10,accuracy(2,:),'b:o')
grid on
xlabel('模型编号')
ylabel('测试集正确率')
title('10个模型的测试集正确率对比(GRNN vs PNN)')
legend('GRNN','PNN')
figure(3)
plot(1:10,time(1,:),'r-*',1:10,time(2,:),'b:o')
grid on
xlabel('模型编号')
ylabel('运行时间(s)')
title('10个模型的运行时间对比(GRNN vs PNN)')
legend('GRNN','PNN')