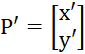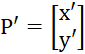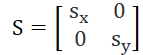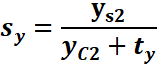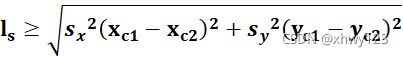简单的一些二维坐标系构建数学模型
1.需求分析
在项目中，需要识别小车三个轮子的相对位置，这就需要对小车抽象出来的二维世界坐标进行缩放平移翻转，并将其转换到控件坐标显示到屏幕上。
2.解决需求
将小车抽象为二维坐标系的一个点P，完成对应数学模型的搭建，实现下列功能：
- 平移变换。
- 另取任意一点C作为缩放中心，对P坐标进行缩放变换。
- 沿X轴对称变换。
- 实现一个三角形从世界坐标系转换到屏幕坐标系，并正常显示.
3.解决问题
1.平移（Translation）
设平移的距离为t x和 t y ,原始坐标为P(x, y)，则将t x和 t y加到原始坐标，可得一个新的坐标位置P’(x', y')，即实现二维坐标系的平移，如下图所示。
其表达式可为：
x'=x+tx y'=y+ty
将一对平移距离( tx , ty )，称为平移向量T。 则可使用下面的列向量来表示坐标位置和平移向量，然后将方程表示成单个矩阵等式。表达成：
; '
; 
2.缩放（Scaling）
改变一个对象的大小，可使用缩放变换。一个简单的二维缩放操作可通过将缩放系数sx
和 sy
与原始坐标位置P(x, y)相乘而得。
其表达式可为：
缩放系数Sx 在x方向缩放对象，而Sy在y方向进行缩放。基本的二维缩放方程也可以写成矩阵形式：
3. 平移、缩放变换拓展
在上面，我们已经完成缩放操作，但还是具有一定的局限性，当
, 
都大于1时，缩放后的坐标位置远离原点O，反之则靠近原点O，这是十分不利的。
于是，我们根据所查资料，使用了固定点(Fixed point)的概念，即缩放变换后不改变位置的点，用以控制缩放后对象的位置，固定点可以是坐标系内的任意一点，这里我们设为点C（
）。
实现过程如下，先进行坐标轴的平移，即将点C作为新的坐标原点，并以C点作为缩放中心，将点P进行缩放，再还原坐标轴得到P‘(x’,y’)，如下图所示。
推导公式如下：
- 将C作为坐标原点:
点C(x,y) => C(x-
, y-
)
点P(x,y) => P(x-
, y-
) 点o(0,0) => 点o(-
, -
)
2.缩放，得到点P’，0’：
点P(x-
, y-
) => P’( 
, 
)
点o(-
, -
) => 点o’( 
, 
)
3.还原缩放中心，获得实际的坐标：
P‘(
, 
)
=》实际坐标P’(
, 
)
点o’(
, 
)
=》实际坐标点o’(
,
)
综上：
其表达式可为：
3. 对称变换
沿着X轴对称变换。
其表达式可为：
4.问题应用
任意三、多边形的缩放翻转平移，将其世界坐标转换到屏幕坐标。
先前讨论的均在世界坐标系当中，但在实际应用场景中，则需要将对象的世界坐标转换成屏幕坐标。
上图为世界坐标系和屏幕坐标系，可以看出屏幕坐标系和世界坐标系是不一样的，屏幕坐标系中以左上角为原点（0，0），大部分的操作系统如Windows，Android，Symbian都是使用这个方案。
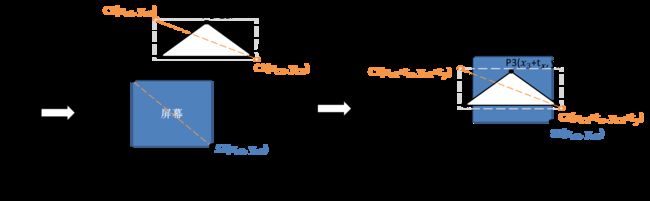
现假设世界坐标系有一三角形对象（其3个顶点分别为P1,P2,P3），想将其转换显示到屏幕上，需要进行下列操作。
1.选定区域。
选定一矩形区域，作为三角形的边界，需要注意的是矩形的尺寸需要略大于三角形。矩形的4个顶点分别为（C1,C2,C3,C4）.
2.将世界坐标系变换到屏幕坐标系
由于屏幕坐标系和世界坐标系不同，所以需要对世界坐标系进行翻转操作，再使用镜像对称(注意：这里的镜像对称并不改变实际坐标，仅起到方便观察作用)。
3.正确的显示到屏幕上
实际生活中，屏幕是由一个一个像素点构成的，且有大小限制，需要通过计算得到合适的参数，对转换后的图像进行平移缩放。
计算如下：
（1）移动到合适位置。
在应用中，我们一般先移动图像，将矩阵的中心点与屏幕中心点重合，如下图所示可得，屏幕中心点为（
，
）矩阵的中心点为（
，
）;
则位移距离
：
综上，表达式可为：
… …
(2)采用对角线法确定缩放比例
使用两点间距离公式
可以得到矩形区域和屏幕的对角线长度，分别设为
和
。
则表达式可为：
*其中，
中xs1
，
可取0。
另设
、
为缩放系数
由S2(2
)可知屏幕可视区域的为
*
，如下图所示，若要将图像铺满，则需进行矩形区域进行缩放。
由于屏幕的形状也是矩形，可以考虑通过缩放，使得C2 (
+
, 
+
)
点跟S2(
)点重合，既可铺满，计算如下：
得到了缩放比例，即可计算三角形三个顶点坐标：
… …
需要注意的是，要正常显示，屏幕的对角线长度应大于等于缩放之后的矩形区域对角线长度。
条件如下：
步骤如下：
