2021李宏毅机器学习笔记--11 explainable ML

摘要

可解释性分为两种，一种是局部可解释性，一般指的是机器说明如何判断这个样例(例如分类问题中，机器如何将一张猫的图片分成猫)；另一种是全局可解释性，一般指的是机器如何对总体进行特征判断(例如分类问题中，机器认为猫长什么样子)

那么为什么我们需要这种可解释性呢？神经网络一般都是黑盒算法这确实，但并不是黑盒本身让我们难受，因为我们人的大脑也是个黑盒；而是如果我们没有一定的解释的话，我们可能会不爽。就例如一个神经网络来计算成绩，如果你分低但是还不知道为什么，那绝对会不爽。而这时如果机器能够解释每道题扣了多少分或者错在哪里这种等等，就不会不服气。也就是说我们期待的不仅是机器知道，还要机器知道为什么知道。

一、局部可解释性

1.1 基本思想

既然我们想要知道机器如何判断，这个问题其实等价于，机器把哪些所谓的特征看的很重要，是这些特征的出现很大程度的影响了机器的判断。
那我们要做的就是，把我们的这些所谓的组成部分来进行修改或者移除等等，来查看影响的效果即可，

下面就使用移除和修改两种不同的操作来进行实验。

1.2 移除组成要素

在图像中的组成要素其实我们大致就可以看作是“一块区域”，这也是CNN的基本假设。那我们就可以移除一部分，然后来记录移除这个部分的影响。如下图，就是将一部分区域涂灰，然后再进行预测，预测的效果在图的下方，与上图涂灰区域的中心对应，预测效果越差就越是冷色调。那我们就可以说明，冷色调的部分很大程度上影响了机器最后判断，也就是所谓的机器学到的内容。

例如上面第三张图中，机器识别出来了狗。如果我们不采用这种方法，我们完全可以不信机器真的是看到了狗才识别出来的，而是把左面的人看成了狗；而采用这种方法，我们看出如果图片中抹去了狗的部分，那机器完全不会在这张图中找到狗，那就说明了机器确实是学到了狗的相关特征。

1.3 改变组成要素

我们可以从另一个角度来去寻找机器更看重哪些信息。对于比较重要的信息，按道理更有可能是对最后的结果影响越大，那么相当于就是，如果输入信息有改变，那么对结果的改变就会更大；如果我们把这个思想取极限，那么就是导数了。根据每个值对目标值得偏微分，我们可以画出一个Saliency Map。

如下图所示，导数越大的地方越明亮。当然，我们这里是计算结果对N个要素的求导而不是单纯的对每个像素求导，因为明显一个像素的改变不会影响结果，也不算是一个特征。

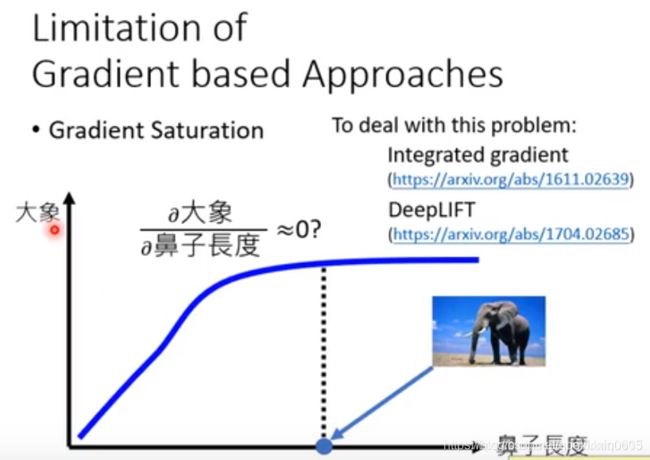
但这种方法存在一个比较大的问题，那就是所谓的 信息冗余现象 ，如下图所示，横轴是鼻子长度而纵轴是说判断为大象的概率。显然，鼻子长是大象的一个极其显著的特点，这里的曲线我们也可以确定机器是关注到这一点的了；但是鼻子长到足够明显了的时候，再长貌似就没有必要了，即信息冗余。如果我们在这个时候看梯度，那竟然几乎是0，也就是说梯度是饱和的（Gradient Saturation），从而和我们的想法相矛盾。如果我们要考虑到对应的前面的梯度，那就只能是连接原点和这个点，就转化成了所谓的移除要素，而不是轻微的改变这个要素了。

1.4 局限性

上述的两种方法看起来确实不错，但是后来大家发现了一个问题，那就是我们完全可以针对这种模型进行攻击。如下图所示，我们就加入了一些肉眼看不到的噪声，也没有改变机器分类的结果，但机器所关注到的部分改变了很多，例如下图中遭受攻击后，机器其实是通过看云来识别出了卡车。虽然我们无法解释这是为什么，但它确实发生了，这就说明了这种方法并不是完全可靠的，而且机器学到的内容可能还是很杂，不是我们想要的效果。

当然，最简单的处理方式是，那我们就对原来的图片加入一个高斯分布的噪音，形成n张图片，然后把这n张图片取平均，来作为说明每个部分的效果。这种方法也被称作SmoothGrad。这里有一个小误区，那就是这样多次加噪声取平均，只是可以更好的说明到底哪个地方的影响力大，而如果是为了用于训练分类器的话，多次取平均与就一次加噪声效果是一样的。

1.5 实例（pokemon vs digimon）

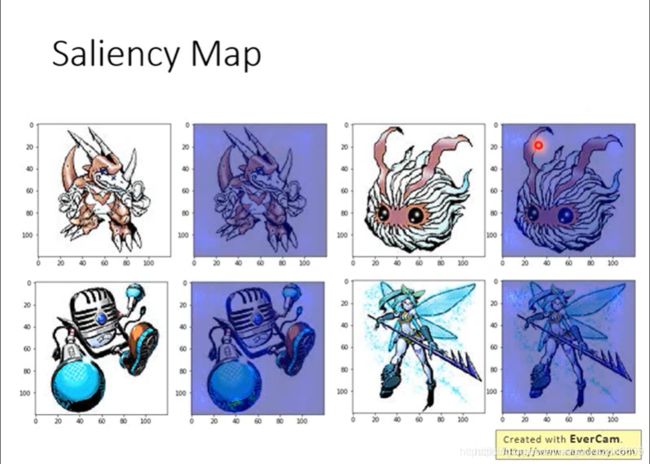
网上有相关数据集。即便是人类，可能也很难分辨一些特殊物种，到底是数码宝贝还是宠物小精灵。机器能否做到呢？胡乱叠了几层 CNN ，训练集准确率98.9%；测试集98.4%。很惊人。于是李老师做了Saliency Map。

李老师回去看了下数据，发现：宝可梦的图片大多是PNG，而Digimon大多是JPEG。这里解释了为什么我们需要Explainable ML。

二、全局可解释性

2.1 反向寻找理想输入

其实在CNN中，我们就提到了全局可解释性。假设我们是在识别MNIST数据集的手写数字，我们既然是想知道在机器眼中，每个数字的样子，那我们就完全可以把结果固定，然后对输入通过梯度下降来得出，到底哪样的输入会使得结果最显

2.2 输入正则化

我们其实是希望，我们最后生成的这些图片，应该是尽量像数字的，从而这就成为了正则化项。比如上图中我们看到，白色像素的点还是太多了，而所有的手写数字图片中，白色的亮点都是比较少的，因此我们就可以在这里加入正则化项，使得我们的整体越暗越好(换句话说就是白色亮点越少越像数字)，最后的结果如下图所示，还是有一定效果的。当然，这一定不是最好的正则化方式，但如果我们人去定义的话，我们很难去找到一个更有说服力的正则化方式。

既然都学这么久机器学习了，我们当然会想到，那我们试图让机器自动去学习这种所谓的正则化方式不就好了吗？而这种正则化的本质，是定义"如何更像一个正常的图片"。我们不好去定义，那就让神经网络去学着去辨认算了，如果神经网络能够将图片很好的分类，那我们就说这是一个正常的图片。所以核算我们的神经网络有两个部分，一个是“生成部分”，利用所谓的反解使得结果就是我们要得到的所谓的损失值的图片；另一个是“分类部分”，用来说我们得到的是不是像正常的图片。但是，这完全不是GAN！而且是分类不是判别！但生成部分本身可以是GAN。

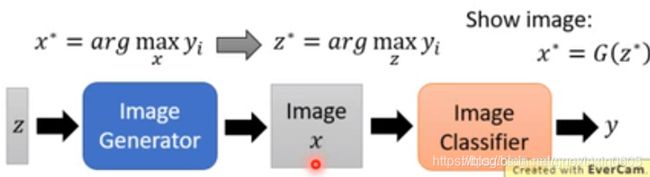当然，这个分类器应该早就训练好了，然后我们产生的图片我们放入这个分类器中，对生成的图片对分类效果和产生效果做一个综合指标，选出合适的。

三、用模型解释模型

另一种可能能更泛化的解释复杂模型的方式，就是用一些操作，使用可解释的模型来解释复杂模型。我们一般用的可解释的模型是线性模型和比较简单的决策树模型。

3.1 使用线性模型

线性模型是最容易解释的模型，不论参数有多少个，每个参数的意义都是能很鲜明的说出这个对应项的情况的。那我们就试图用线性模型直接去尽量的切合我们的神经网络的结果。
然而实际上，线性模型过于简单，很多时候根本无法胜任这个任务。我们只能退而求其次，我们希望看到一个区域内的情况，然后来做出我们的决策。因此，LIME就应运而生。当然，这个所谓的局部的大小，可能会对模型有极大的影响，因此调参也成为了一项技术活。
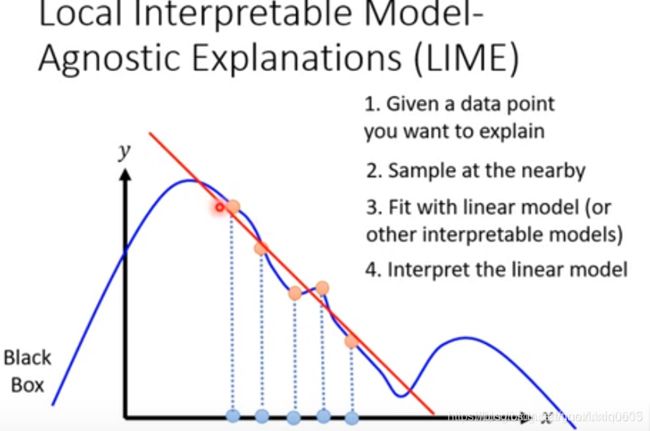当然，在我们的图像处理中，这里的第二步也会有细节问题。对于一张图片，每个维度是一个像素或者是一个像素的一种颜色。这个所谓的附近点，对于一张图片而言，改动太少了，机器辨认的结果依然一直很好，这就导致了我们这里硬要求的话效果很难很好，因为本来就都说明不了什么差异。
因此我们就是，把一张图片分成多个部分，然后我们直接去掉一些部分，来作为所谓的相邻区域的样本。注意，这里有个有趣的事情，就是如何去划分这些部分。其实这是图形学的一些知识，但总之就是和色调的变化相关。
看下图，我们现在则可以分析linear model这些参数：

如果权重接近0，则说明这个区域与青蛙无关；
如果正数，则说明这个区域与青蛙相关；
如果负数，则说明这个区域让机器认为其不是青蛙。

3.2 使用决策树

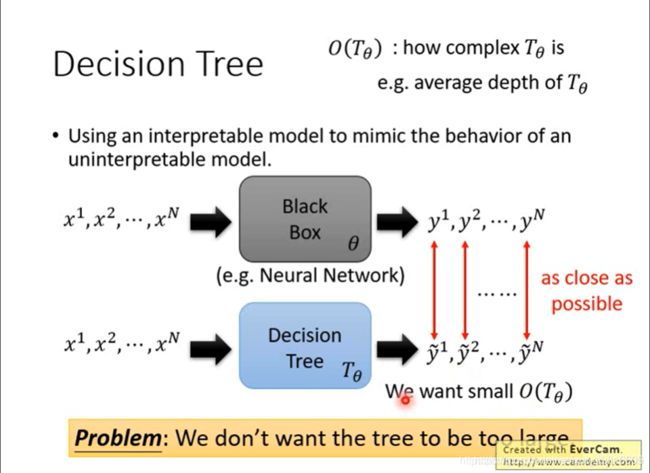决策树模型和线性模型的区别就是，如果树足够复杂，那么理论上多复杂的神经网络都是可以被模拟的。所以我们考虑的不应该再是分块处理来试图想办法契合神经网络的结果，而是我们要综合考虑两个指标：一个是决策树的契合程度，另一个是决策树的复杂程度(当然定义有很多种，比如所有点平均的深度)。

通过式子我们可以看出，这也可以说是所谓的正则化，被称为树正则化。最后有一个细节问题就是，正则化项是离散的，这次确实没办法微分了。因此paper中选择的方式是训练了另一个神经网络，那个神经网络用于把主神经网络的参数作为输入，预测树的深度，然后对主神经网络的参数做微分。

总结

可解释机器学习的目的是让现有的高精度深度学习模型增强可解释性，可解释性分为局部可解释性和全局可解释性。局部可解释性其实就是对组成部分进行修改和移除两种做法，这两张做法看起来不错。但也有一定的局限性，比如可以针对训练的模型进行攻击。全局可解释性之前有过接触，包括反向寻找理想输入和输入正则化。也可以使用可解释的模型来解释复杂模型，我们一般用的可解释的模型是线性模型和比较简单的决策树模型。那么为什么我们需要这种可解释性呢？源于我们期待的不仅是机器知道，还要机器知道为什么知道。