Model-Agnostic Meta-Learning (MAML)模型介绍及算法详解
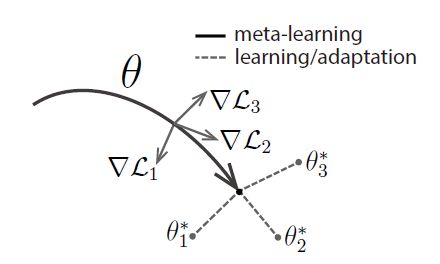
整理自:
Frank Tian 回答
首先,我们先从Meta Learning的概念说起。
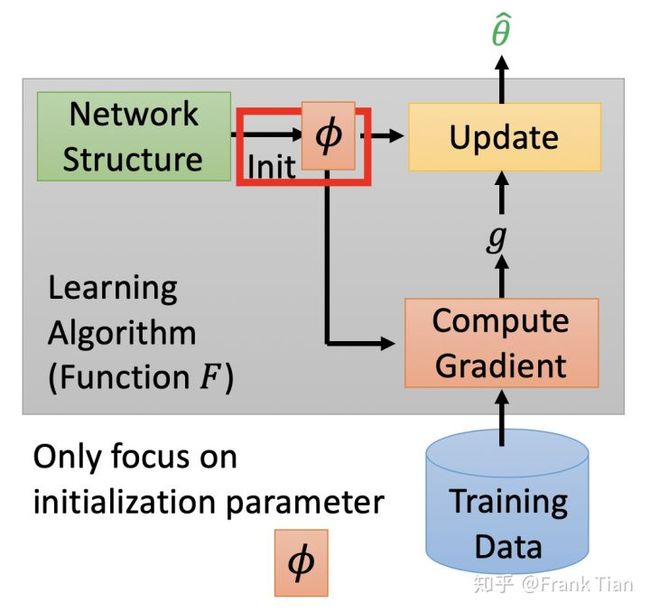
原始的机器学习的流程被认为是下面这这样的:
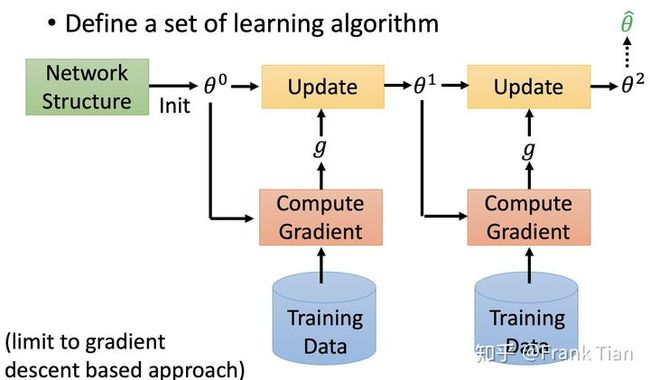
也就是我们根据我们先验知识设计网络架构和参数初始化方法,从Training Data 中得到参数的梯度,使用一阶条件调整参数。
因为网络架构已经是提前设计好的,我们学习的最终输出其实就是参数。
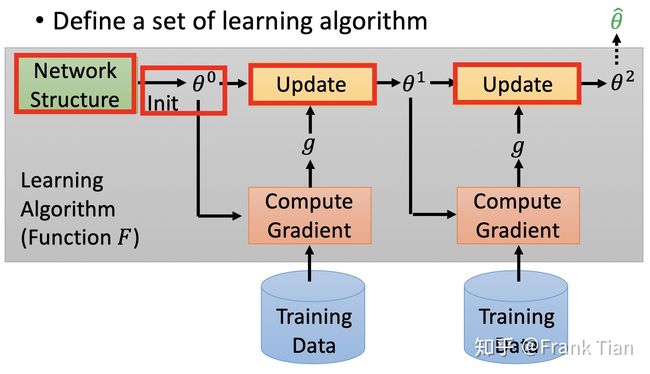
图中红框内的都是人类之前设计好的,Meta Learning 的目标就是学习这些是如何设计的。
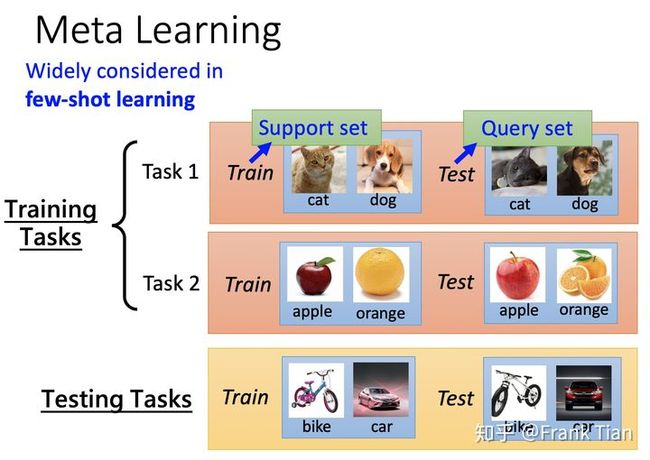
Meta Learning的任务是输入,现阶段成熟的方法一般默认这些任务是同类的。例如图像分类。
输入的训练集可以是十个图像分类任务,这些任务有自己的训练集和测试集,但是我们在这里称为 Support Set 和 Query Set
而测试集可以是两个额外的任务,当然他们也有自己的Support set 和 Query set。
Machine Learning 的训练和测试数据如下:

Meta Learning 的训练和测试数据如下:
在 Machine Learning 中我们定义损失函数为 l = L ( f ) l = L(f) l=L(f) , f f f 表示这个模型,损失函数 L L L 是一个泛函,通常我们用测试数据经过模型的输出和原来的label的差异作为损失函数的估计。
而Meta Learning中,我们用这些 l l l 的和,估计Meta Learning的损失:
L ( F ) = ∑ i = 0 N l n L(F) = \sum_{i=0}^{N} l^n L(F)=i=0∑Nln
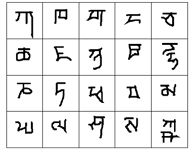
在Meta Learning中,我们常用Omniglot作为数据集训练,Omniglot有1623个characters,每个character有20个examples。
characters如下:

而examples指的是同样一个character经过不同的人写出来的结果:

Mate Learning的任务被称为N-ways K-shot classification,N指的是有多少个类别,K指的是每个类别有多少个sample。
Meta Learning常常和Few-shot Learning一起出现,Few-shot Learning指的是样本特别少的Machine Learning。
例如一个20-ways 1-shot classification,就是一共有20个类别,每个类别只有一个训练样本。往往这样的问题用传统的Machine Learning是很难解决的。20-ways 1-shot classification的一个例子如下:
Support set:
Query set:

而MAML就是一种决定如何初始化参数的方法。
它默认要求了不同任务的网络模型是一样的,更确切的说,它没有“根据训练集生成初始化参数”的能力,它对所有任务的初始化参数是相同的。
也就是说,它其实是找到了对于所有的任务,最好的一种参数初始化的方法。并让所有任务都按照这种方法进行参数初始化。
这当然要求模型的结构是相同的了,不然根本没有办法使用同样的参数。
我们设初始化的参数为 ϕ \phi ϕ,每个任务的模型一开始的参数都是 ϕ \phi ϕ,经过训练后,参数就会变成 θ ^ n \hat{\theta}^n θ^n ,而用 l n ( θ ^ n ) l^n(\hat{\theta}^n) ln(θ^n)表示每个任务的损失。
那么,对于这个Meta Learning而言,整体的损失函数应该是 ϕ \phi ϕ 的函数:
L ( ϕ ) = ∑ n = 1 N l n ( θ ^ n ) L(\phi) = \sum_{n=1}^{N} l^n(\hat{\theta}^n) L(ϕ)=n=1∑Nln(θ^n)
当然如果我们把 ϕ \phi ϕ 看作参数, L L L 就是函数,把 ϕ \phi ϕ 看作函数, L L L 就是泛函,不过问题不大。而对于单一的一个任务而言, ϕ \phi ϕ 被视为超参数。
回忆一下我们之所以能很有效的调节参数,而没办法高效的调节超参数,就是因为我们没办法计算超参数的梯度,而MAML则是基于一些假设,使我们可以计算 ϕ \phi ϕ 的梯度。
一旦我们可以计算 ϕ \phi ϕ 的梯度,就可以直接更新 ϕ \phi ϕ :
ϕ ← [ ϕ − η ▽ ϕ L ( ϕ ) ] \phi \leftarrow [\phi - \eta\bigtriangledown_{\phi } L(\phi ) ] ϕ←[ϕ−η▽ϕL(ϕ)]
而所谓的假设即是:每次训练只进行一次梯度下降。
这个假设听起来不可思议,但是却也有一定的道理,首先我们只是在Meta Learning的过程中只进行一次参数下降,而真正学习到了很好的 ϕ \phi ϕ 之后自然可以进行多次梯度下降。
只考虑一次梯度下将的原因有:
- Meta Learning会快很多 ;
- 如果能让模型只经过一次梯度下降就性能优秀,当然很好 ;
- Few-shotlearning的数据有限,多次梯度下降很容易过拟合 ;
- 刚才说的可以在实际应用中多次梯度下降.
如果只经历了一次梯度下降,模型最后的参数就会变成:
θ ^ = θ − ϵ ▽ ϕ l ( ϕ ) \hat{\theta} = \theta - \epsilon\bigtriangledown_{\phi }l(\phi ) θ^=θ−ϵ▽ϕl(ϕ)
当然因为 l l l 的不同,最后不同任务的 θ ^ \hat{\theta} θ^ 也会不一样,准确来说应该是:
θ ^ n = θ − ϵ ▽ ϕ l n ( ϕ ) \hat{\theta}^n = \theta - \epsilon\bigtriangledown_{\phi }l^n(\phi ) θ^n=θ−ϵ▽ϕln(ϕ)
现在我们已经有 L ( ϕ ) = ∑ n = 1 N l n ( θ ^ n ) L(\phi) = \sum_{n=1}^{N} l^n(\hat{\theta}^n) L(ϕ)=∑n=1Nln(θ^n),下一步就是计算 θ \theta θ 关于 L L L 的梯度。
我们有:
▽ ϕ L ( ϕ ) = ▽ ϕ ∑ i = 1 N l n ( θ ^ n ) = ∑ n = 1 N ▽ ϕ l n ( θ ^ n ) \bigtriangledown_{\phi}L(\phi) = \bigtriangledown_{\phi}\sum_{i=1}^{N} l^n(\hat{\theta}^n)=\sum_{n=1}^{N}\bigtriangledown_{\phi} l^n(\hat{\theta}^n) ▽ϕL(ϕ)=▽ϕi=1∑Nln(θ^n)=n=1∑N▽ϕln(θ^n)
现在的问题是如何求 ▽ ϕ l n ( θ ^ n ) \bigtriangledown_{\phi} l^n(\hat{\theta}^n) ▽ϕln(θ^n) ,略去上标 n n n,有:
▽ ϕ l ( θ ^ ) = [ ∂ l ( θ ^ ) ∂ ϕ 1 ∂ l ( θ ^ ) ∂ ϕ 2 ⋮ ∂ l ( θ ^ ) ∂ ϕ i ⋮ ] \bigtriangledown_{\phi} l(\hat{\theta})=\left[ \begin{matrix} \frac{\partial l(\hat{\theta})}{\partial \phi_1}\\ \frac{\partial l(\hat{\theta})}{\partial \phi_2}\\ {\vdots}\\ \frac{\partial l(\hat{\theta})}{\partial \phi_i}\\ {\vdots} \end{matrix} \right] ▽ϕl(θ^)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡∂ϕ1∂l(θ^)∂ϕ2∂l(θ^)⋮∂ϕi∂l(θ^)⋮⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤
注意 l l l 是 θ \theta θ 的函数,而 θ \theta θ 又和每一个 ϕ i \phi_i ϕi 有关,因此有:
∂ l ( θ ^ ) ∂ ϕ i = ∑ j ∂ l ( θ ^ ) ∂ θ ^ j ∂ l ( θ ^ j ) ∂ ϕ i \frac{\partial l(\hat{\theta})}{\partial \phi_i} = \sum_{j}\frac{\partial l(\hat{\theta})}{\partial \hat{\theta}_j} \frac{\partial l(\hat \theta_j)}{\partial \phi_i} ∂ϕi∂l(θ^)=j∑∂θ^j∂l(θ^)∂ϕi∂l(θ^j)
也就是说,每一个 ϕ i \phi_i ϕi 通过影响不同的 θ i \theta_i θi,从而影响到 l l l:
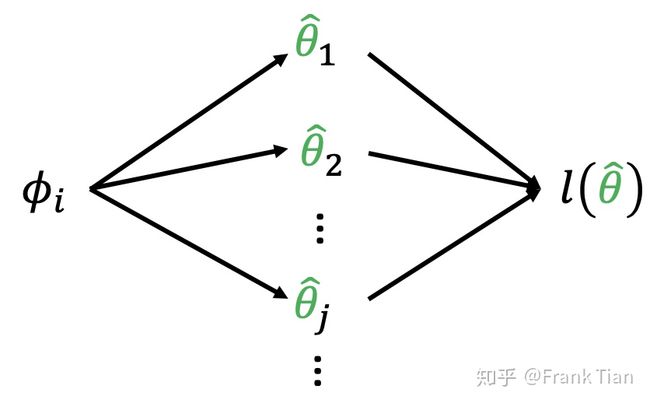
l l l 和 θ \theta θ 的关系是很直接的,我们可以直接求 ∂ l ( θ ^ ) ∂ θ ^ j \frac{\partial l(\hat{\theta})}{\partial \hat{\theta}_j} ∂θ^j∂l(θ^) ,现在的问题是怎么求 ∂ l ( θ ^ j ) ∂ ϕ i \frac{\partial l(\hat \theta_j)}{\partial \phi_i} ∂ϕi∂l(θ^j) 。
注意 ϕ \phi ϕ 和 θ \theta θ 的关系也是显然的:
θ ^ = ϕ − ϵ ∇ ϕ l ( ϕ ) \hat \theta = \phi - \epsilon \nabla_{\phi}l(\phi) θ^=ϕ−ϵ∇ϕl(ϕ)
把向量的形式展开:
θ ^ j = ϕ j − ϵ ∂ l ( ϕ ) ∂ ϕ j \hat \theta_j = \phi_j - \epsilon \frac{\partial l(\phi)}{\partial \phi_j} θ^j=ϕj−ϵ∂ϕj∂l(ϕ)
我们考虑 i ≠ j i \neq j i=j :
∂ ( θ ^ j ) ∂ ϕ i = − ϵ ∂ l 2 ( ϕ ) ∂ ϕ i ∂ ϕ j \frac{\partial (\hat \theta_j)}{\partial \phi_i} = - \epsilon \frac{\partial l^2(\phi)}{\partial \phi_i \partial \phi_j} ∂ϕi∂(θ^j)=−ϵ∂ϕi∂ϕj∂l2(ϕ)
而当 i = j i = j i=j :
∂ ( θ ^ j ) ∂ ϕ i = 1 − ϵ ∂ l 2 ( ϕ ) ∂ ϕ i ∂ ϕ i \frac{\partial (\hat \theta_j)}{\partial \phi_i} = 1 - \epsilon \frac{\partial l^2(\phi)}{\partial \phi_i \partial \phi_i} ∂ϕi∂(θ^j)=1−ϵ∂ϕi∂ϕi∂l2(ϕ)
当然到此为止已经把梯度计算出来了,但是在MAML的论文中其实做了简化,它直接不计算二阶条件。
∂ ( θ ^ j ) ∂ ϕ i = − ϵ ∂ l 2 ( ϕ ) ∂ ϕ i ∂ ϕ j ≈ 0 \frac{\partial (\hat \theta_j)}{\partial \phi_i} = - \epsilon \frac{\partial l^2(\phi)}{\partial \phi_i \partial \phi_j} \approx 0 ∂ϕi∂(θ^j)=−ϵ∂ϕi∂ϕj∂l2(ϕ)≈0
∂ ( θ ^ j ) ∂ ϕ i = 1 − ϵ ∂ l 2 ( ϕ ) ∂ ϕ i ∂ ϕ i ≈ 1 \frac{\partial (\hat \theta_j)}{\partial \phi_i} = 1 - \epsilon \frac{\partial l^2(\phi)}{\partial \phi_i \partial \phi_i} \approx 1 ∂ϕi∂(θ^j)=1−ϵ∂ϕi∂ϕi∂l2(ϕ)≈1
那么原来的偏导近似为:
∂ l ( θ ^ ) ∂ ϕ i = ∑ j ∂ l ( θ ^ ) ∂ θ ^ j ∂ l ( θ ^ j ) ∂ ϕ i ≈ ∂ l ( θ ^ ) ∂ θ ^ i \frac{\partial l(\hat{\theta})}{\partial \phi_i} = \sum_{j}\frac{\partial l(\hat{\theta})}{\partial \hat{\theta}_j} \frac{\partial l(\hat \theta_j)}{\partial \phi_i} \approx \frac{\partial l(\hat{\theta})}{\partial \hat{\theta}_i} ∂ϕi∂l(θ^)=j∑∂θ^j∂l(θ^)∂ϕi∂l(θ^j)≈∂θ^i∂l(θ^)
整个梯度就可以近似为:
▽ ϕ l ( θ ^ ) = [ ∂ l ( θ ^ ) ∂ ϕ 1 ∂ l ( θ ^ ) ∂ ϕ 2 ⋮ ∂ l ( θ ^ ) ∂ ϕ i ⋮ ] ≈ [ ∂ l ( θ ^ ) ∂ θ ^ 1 ∂ l ( θ ^ ) ∂ θ ^ 2 ⋮ ∂ l ( θ ^ ) ∂ θ ^ i ⋮ ] = ∇ θ ^ l ( θ ^ ) \bigtriangledown_{\phi} l(\hat{\theta})=\left[ \begin{matrix} \frac{\partial l(\hat{\theta})}{\partial \phi_1}\\ \frac{\partial l(\hat{\theta})}{\partial \phi_2}\\ {\vdots}\\ \frac{\partial l(\hat{\theta})}{\partial \phi_i}\\ {\vdots} \end{matrix} \right] \approx \begin{bmatrix} \frac{\partial l(\hat{\theta})}{\partial \hat\theta_1}\\ \frac{\partial l(\hat{\theta})}{\partial \hat\theta_2}\\ {\vdots}\\ \frac{\partial l(\hat{\theta})}{\partial \hat\theta_i}\\ {\vdots} \end{bmatrix} = \nabla_{\hat\theta}l(\hat\theta) ▽ϕl(θ^)=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎡∂ϕ1∂l(θ^)∂ϕ2∂l(θ^)⋮∂ϕi∂l(θ^)⋮⎦⎥⎥⎥⎥⎥⎥⎥⎥⎤≈⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡∂θ^1∂l(θ^)∂θ^2∂l(θ^)⋮∂θ^i∂l(θ^)⋮⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤=∇θ^l(θ^)
那么整个MAML的过程其实就很简单了:
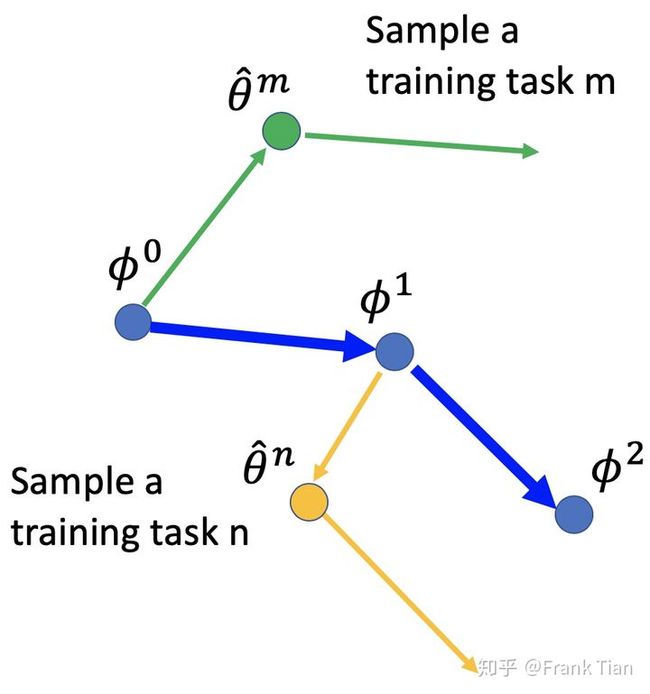
从 ϕ 0 \phi^0 ϕ0 开始,先用一个batch的任务训练(这里任务就相当于数据了),假设只用了一个任务,即任务m。
那么先用 ϕ 0 \phi^0 ϕ0 作为初始化参数,用task m的数据作为训练集,梯度下降一次,得到了 θ ^ m \hat{\theta}^m θ^m ,这是已经训练好的模型了(我们假设只梯度下降一次)。
然后我们要得到模型关于 θ ^ m \hat{\theta}^m θ^m 的梯度信息,那就再求一次梯度,但是我们就不用这个梯度对 θ \theta θ 梯度下降了,而是对 ϕ \phi ϕ 梯度下降。
不停的计算不同的task的梯度,对 ϕ \phi ϕ 进行更新,就得到了最终的 ϕ \phi ϕ 。
这就是MAML的思想。
参考:
[1] Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks