动态规划算法的例子

如果是计算机科班出身的话，动态规划可能已经听过，研究生的课程和本科生的课程的区别在于采用的教材难度更加大一些。更强调一些经典问题和在此基础上升级的问题。动态规划和分治算法有很多地方是相像的。

一、引子

1、最短路径问题

问题：
输入：$$起点集合S_1,S_2,...,S_n，终点集合T_1,T_2,...,T_m，$$
中间结点集，
边集 E，对于任意边 e 有长度
输出：一条从起点到终点的最短路

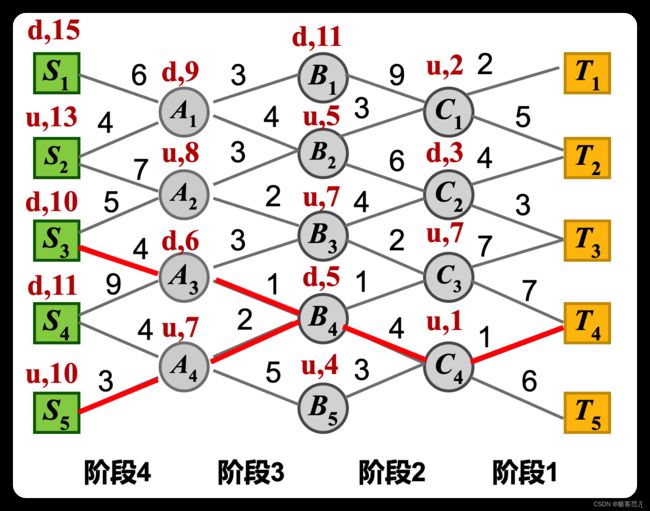
2、实例

起点和终点的排列，拓扑图是这样的，比如从S3开始，必须要经过中间的A2或者A3，不管选择途径哪个点，都会到达B这一层，不管在B上途径哪个点，都会到达C这一层，不管在C上途径哪个点，都会到达终点。

这里面涉及的问题就是多阶段的，每个阶段这样的基础上来做决策，这样的话能不能找到一个最短的路呢？最短的路应该怎么样去找呢？

当然我们可以采用一个蛮力的算法

3、算法设计

（1）蛮力算法：考察每一条从某个起点到某个终点的路径，计算长度，从其中找出最短路径

在上述实例中，如果网络的层数为 k，那么路径条数将接近于$$2^k$$
（2）动态规划算法：多阶段决策过程。
每步求解的问题是后面阶段求解问题的子问题。每步决策将依赖于以前步骤的决策结果

4、动态规划求解

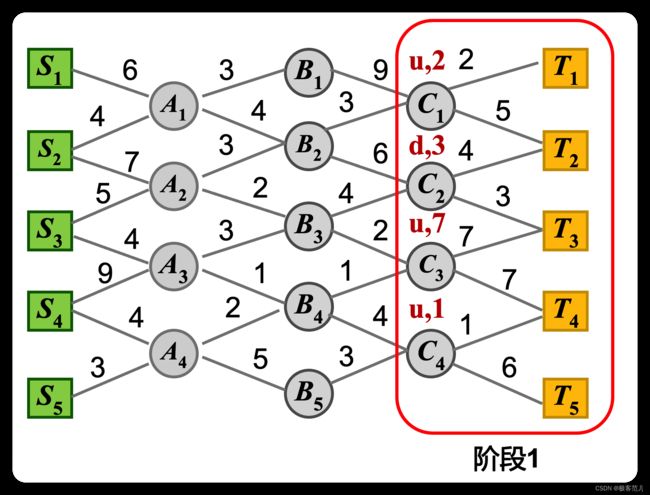
（1）阶段1：

从C到T的这个过程，这个过程就是跟目前所在的位置有关系，从C1点到T1点或者T2这个点，最短的走法就是up（往上走）而且代价是2。

在上面的数字表示距离长短，这些所有的点，不管从哪个点出发，一定会到达C这一层，从这一层往后走，一定要经过这个阶段来，前面继续走，走到C2点，C2点的选择一定是down（往下走），这是最好的走法。

C3同理，up（往上走）代价为7，C3两条道路的长短是一样的

C4同理，up（往上走）代价为1

注：up、down的标记就是向上/下走

这个就叫做一个阶段，阶段1是和阶段2有关系。因为要到C层是必经的结果，怎么样才能到C呢？那一定要经过B这一层
（2）阶段2:

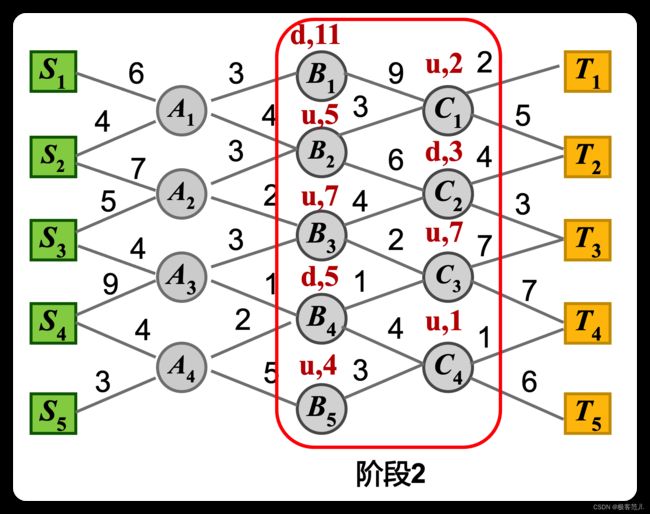
B1点只能down往下走，因为它只有这个路径走到C，到达C1以后再怎么走我们认为是已知的了。C1以后再怎么走达到最短，假定是已知的（其实是可以算出来的，因为一定要经过C1到达终点）后面怎么走就不用管了，因为已经达到结果了（一定是up），所以代价为11（9+2）

走的C这一层其实是要借助C这一层以后的结果，C这一层在前面找路的时候一定要看后拿能不能走的好的，也就是可能性。

B2点也是这么考虑，B2如果往上走，就是3个单位的路径加上C1这个点，C1这个点最好的走法是up向上走2个单位的距离，所以代价为5（3+2）。那么往下走呢？往下走到C2点，C2点的最短代价是3，3+6=9，那就不能往下走，因为从B2点走到C2之后到达终点最小代价是3，整体加起来是9(9 > 5)，所以到B2点之后只能向上走。

B3点同理up到达C2

B4点同理down到达C4

B5点同理up到达C4

在做决策，利用了阶段1的结果，因为阶段1的结果就已经表达阶段1到达终点最短就是这样，后面阶段的可能性是要考虑的。

（3）阶段3：

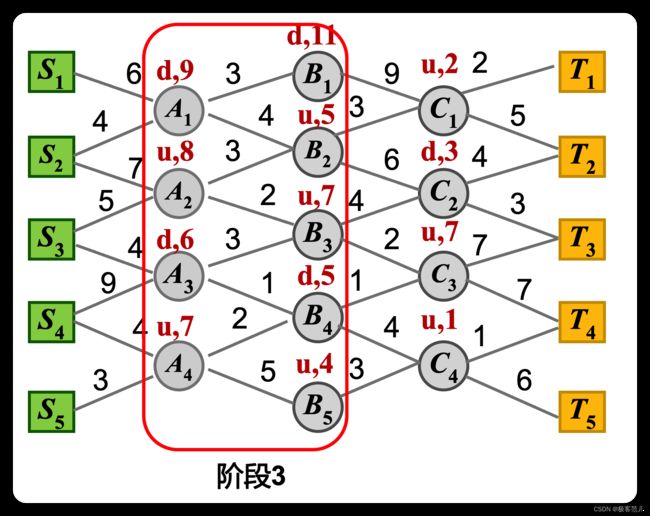
在由A到B的过程，因为A一定要经过B的，由B往后走它的可能性（最优路径）是已知的，而且代价都知道。

A1点，相当于每一次在A1在考察的时候，往上走是3+11，因为B往后怎么走不知道，所以代价14（3+11）代价比较大，如果A1走到B2是4个单位的代价，这个代价是比3大的，当前的代价大，但是走到B2以后到终点的代价是5个单位了，代价9（4+5），所以不要看到眼前的困难，眼前这一步虽然困难，但是只要打通这个环节，后面走起来就非常轻松了，整体代价就小了，所以克服眼前的困难眼看到长远的发展。

多阶段决策的时候是当前代价其实并不是注重决策的依据，而是整体衡量。

A2点也是如此。达到A2点以后往上走有3个单位的代价，但实际上整体代价是8（3+5），A2如果走到B3点，往下走虽然代价小，但是整体代价是9（2+7），所以还是往上走。

A3点同理，向下走

A4点同理，向下走。

这个阶段也做完了，就把A这些点到终点的最短代价找到了。最后进入到最开始的那一层，这一层被称之为阶段4

（4）阶段4：

S1点只有一种选择，往下走代价15（6+9）

S2点往上走代价13（4+9），往下走的代价是15（7+8），所以想上走是最优路径。

S3同理，向下走代价10

S4同理，向下走代价11

S5同理，想上走代价10

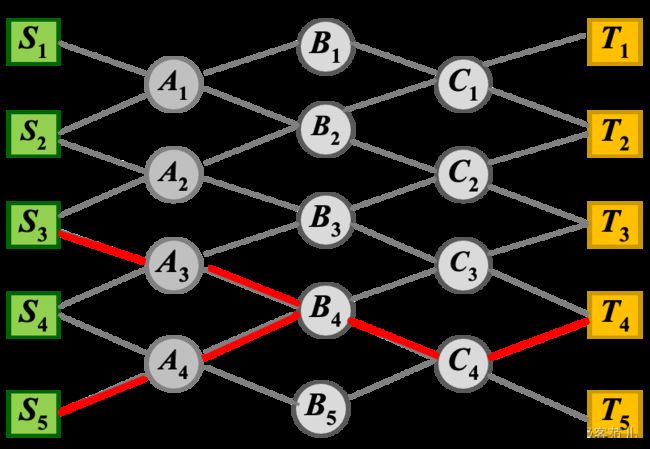
所以现在结果就出来了，如果从S1出发，首先往下走到达A1点，然后向下走到达B2点，接着想上走到达C1，最后想上走到达T1，最终代价最小是15。

这个就叫多阶段的决策，最后求解把从最开始把记录的符号S3->T4之间有一条最短路径是10；以及S5->T4之间有一条最短路径是10。

5、子问题界定

（1）后边界不变, 前边界前移
关于子问题，后面边界不变，前面的边界在前移的过程中，不停的产生一个决策，然后基于决策的基础上再来做决策，子问题和原问题的性质还是有相似的，依然是在做最短距离。

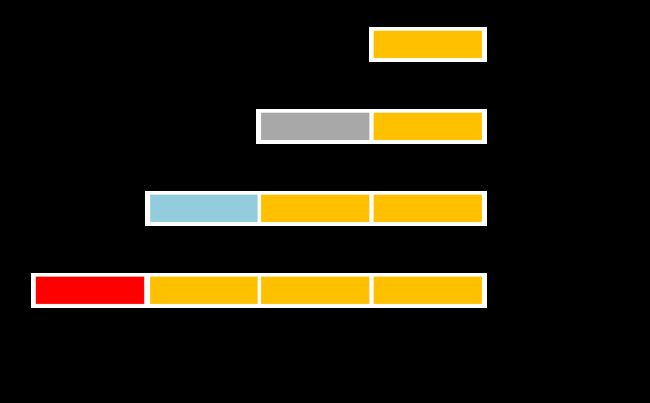
原问题是S->T，现在C->T也是子问题，从B->T也是子问题，从A->T还是子问题。只不过这个子问题的规模要小一点，这些子问题之间是一层一层的，嵌套起来。

（2）最短路长的依赖关系
其实用公式来写也是这样的一种写法，在C层由C出发到T的最小

优化函数值之间存在依赖关系

依赖关系是这个阶段的决策，比如说在第一阶段，在C->T的过程中，它的往上往下的决策以及它的路径代价，是要考虑的，到底往上还是往下，当前考虑的时候，其实是要把上一个阶段所决策的结果作为当前的一个考量，当前的考量，当前的决策是要依赖于未来的发展的基础上做考虑的，每个阶段有一个依赖关系。

6、优化原则

最优子结构性质
（1）优化函数的特点：任何最短路的子路径相对于子问题始、终点最短

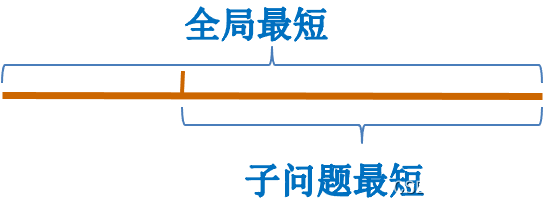
（2）优化原则：一个最优决策序列的任何子序列本身一定相对于子序列的初始和结束状态的最优决策序列

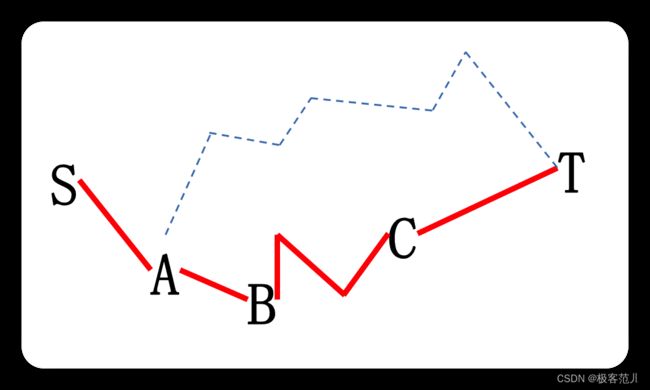
例如实例S->T，如果找到一个条最优路径，中间经过A、B、C层，这个是个决策序列（实线），决定怎么走，如果把前面这段S->A这段不看，那么从A出发到T的决策也在里面。

如果从A出发到T，它的最优决策如果是这条路径（虚线），整体代价比下面这条（实线）代价要小，那这个地方就出现矛盾了，就发现这个不是最优决策，但是我们一开始假定了S->T就是路径（实线）是最优的。那现在又找到了另外一条最优的（虚线），把这条最优的部分替换，替换以后发现问题，最开始的假设就有问题最开始就不是最优的，所以就把它替换成最优的好了。所以这条路径（虚线）是不可能存在的。

那么现在就有一个最优子结构的问题，原问题它的决策序列，对子问题而言（A-T、B->T、C->T）也是它的最优决策，相当于子问题而言也是它的最优决策，其实把时间范围缩小一点，在任何一个时间范围内其实做的决策相对那一段时间而言也是最优的，如果不是那就可以替换，拿那段时间来替换，我们把这歌性质称之为左右子结构性质。

二、反例

求总长模10的最小路径

1、动态规划算法的解：下, 上, 上, 上

2、最优解：下, 下, 下, 下

不满足优化原则，不能用动态规划

三、总结

动态规划暗含着最优子结构，这个也是用来判断一个问题到底能不能用动态规划的一个重要的依据，但是这个事情不太好判断，是需要有很多的练习。

动态规划(Dynamic Programming)

• 求解过程是多阶段决策过程，每步处理一个子问题，可用于求解组合优化问题
• 适用条件：问题要满足优化原则或最优子结构性质，即：一个最优决策序列的任何子序列本身一定是相对于子序列的初始和结束状态的最优决策序列